河北省石家庄市赵县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-19 类型:期末考试
一、单选题
-
1. 下列调查方式中最适合的是( )A、要了解一批节能灯的使用寿命,采用全面调查方式 B、调查你所在班级的同学的身高,采用抽样调查方式 C、环保部门调查老哈河某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用全面调查方式2. 当x是怎样实数时,式子在实数范围内有意义( )A、 B、 C、 D、3. 某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )A、数100和η , t都是变量 B、数100和η都是常量 C、η和t是变量 D、数100和t都是常量4. 下列式子为最简二次根式的是( )A、 B、 C、 D、5. 如图,下列四组条件中.不能判定四边形ABCD是平行四边形的是( )
 A、AB=DC,AD=BC B、 , C、 , D、 ,6. 某市在一次空气污染指数抽查中,收集到10天的数据如下:61,75,70,56,81,91,92,91,75,81,该组数据的中位数是( )A、78 B、81 C、91 D、77.37. 下列运算正确的是( )A、 B、 C、 D、8. 函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 下列各曲线中能表示y是x的函数的是( )A、
A、AB=DC,AD=BC B、 , C、 , D、 ,6. 某市在一次空气污染指数抽查中,收集到10天的数据如下:61,75,70,56,81,91,92,91,75,81,该组数据的中位数是( )A、78 B、81 C、91 D、77.37. 下列运算正确的是( )A、 B、 C、 D、8. 函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 下列各曲线中能表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
10. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )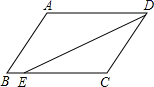 A、2cm B、4cm C、6cm D、8cm11. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )A、1:2:3:4 B、1:2:2:1 C、1:1:2:2 D、2:1:2:112. 在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是( )A、
A、2cm B、4cm C、6cm D、8cm11. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )A、1:2:3:4 B、1:2:2:1 C、1:1:2:2 D、2:1:2:112. 在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是( )A、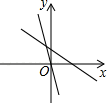 B、
B、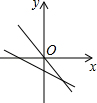 C、
C、 D、
D、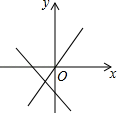 13.
13.如图,AB是池塘两端,设计一方法测量AB的距离,取点C,连接AC、BC,再取它们的中点D、E,测得DE=15米,则AB=( )米.
 A、7.5 B、15 C、22.5 D、3014. 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )
A、7.5 B、15 C、22.5 D、3014. 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( ) A、2 B、4 C、 D、15. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得关于x,y的二元一次方程组的解是( )
A、2 B、4 C、 D、15. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得关于x,y的二元一次方程组的解是( ) A、 B、 C、 D、16. 如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
A、 B、 C、 D、16. 如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
17.(1)、点M(a,2)是一次函数y=2x-3图像上的一点,则a= .(2)、已知一次函数y=(m-2)x+m-3的图象经过第一,第三,第四象限,则m的取值范围 .18. 若直角三角形的两边长为3和4,则第三边长为 .19. 如图,在平面直角坐标系中,点 , , ……,都在x轴上,点 , , ……在直线y=x上, , , , , 都是等腰直角三角形,如果 , 则点的坐标是 .

三、解答题
-
20. 计算:(1)、(2)、已知a= +2,b= ﹣2,求a2﹣b2的值.21.(1)、发现.① ;② ;③ ;……写出④;⑤;(2)、归纳与猜想.如果n为正整数,用含n的式子表示这个运算规律;(3)、证明这个猜想.22. 某校开展了“学党史,知党恩,跟党走”的知识竞赛.现从该校七、八年级中各随机抽取20名学生的竞赛成绩进行调查:
[收集数据]七年级:70,74,74,76,78,78,80,80,82,85,88,88,94,95,98,100,100,100,100,100;
八年级:64,68,70,72,74,80,82,82,84,86,90,92,98,98,98,100,100,100,100,100,100
[分析数据]两组数据的平均数、众数、中位数如表:
年级
平均数
众数
中位数
七年级
87
100
a
八年级
87
b
88
根据以上信息,解答下列问题:
(1)、直接写出上述表格中a,b的值;(2)、根据以上样本数据,你认为该校七、八年级中哪个年级学生对“党史”掌握较好?请说明理由;(3)、若成绩在80分以上(含80分)为优秀,该校七、八年级共有800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?23. 如图,在四边形ABCD中,AB=BC=3,CD= ,DA=5,∠B=90°,求∠BCD的度数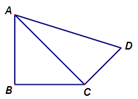 24. 甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图,线段 、折线 分别表示两车离甲地的距离 (单位:千米)与时间 (单位:小时)之间的函数关系.
24. 甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图,线段 、折线 分别表示两车离甲地的距离 (单位:千米)与时间 (单位:小时)之间的函数关系.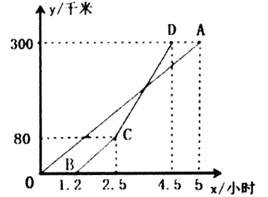 (1)、线段 与折线 中,(填线段 或折线 )表示货车离甲地的距离 与时间 之间的函数关系.(2)、求线段 的函数关系式(标出自变量 取值范围);(3)、货车出发多长时间两车相遇?25. 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)、线段 与折线 中,(填线段 或折线 )表示货车离甲地的距离 与时间 之间的函数关系.(2)、求线段 的函数关系式(标出自变量 取值范围);(3)、货车出发多长时间两车相遇?25. 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点. (1)、求证:△MBA≌△NDC;(2)、四边形MPNQ是什么样的特殊四边形?请说明理由.26. “一方有难,八方支援”.在抗击“5.12”汶川特大地震灾害中,某市组织20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满.根据表中提供的信息,解答下列问题:
(1)、求证:△MBA≌△NDC;(2)、四边形MPNQ是什么样的特殊四边形?请说明理由.26. “一方有难,八方支援”.在抗击“5.12”汶川特大地震灾害中,某市组织20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满.根据表中提供的信息,解答下列问题:物资种类
食品
药品
生活用品
每辆汽车运载量(吨)
6
5
4
每吨所需运费(元/吨)
120
160
100
(1)、设装运食品的车辆数为x,装运药品的车辆数为y.求y与x的函数关系式;(2)、如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么车辆的安排有哪几种方案?(3)、在(2)的条件下,若要求总运费最少,应采用哪种安排方案?并求出最少总运费.