河北省石家庄市长安区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列调查中，适合采用普查的是（）

A、调查北京冬奥会开幕式的收视率 B、调查某批玉米种子的发芽率 C、调查某市居民进行垃圾分类的情况 D、调查疫情期间某超市工作人员的健康码

查看试题解析
2. 在平面直角坐标系中，点A(a，2)在第二象限内，则 $a$ 的取值可以是（）

A、1 B、-3 C、4 D、4或-4

查看试题解析
3. 在 $▱ A B C D$ 中， $∠ A ： ∠ B = 2 ： 3$ ，则 $∠ C$ 的度数为（）

A、 $36 °$ B、 $72 °$ C、 $108 °$ D、 $144 °$

查看试题解析
4. 如图，直线 $l_{1}$ ： $y = 2 x - 1$ 与直线 $l_{2}$ ： $y = k x + b (k \neq 0)$ 相交于点 $P (2 ， 3)$ ，则关于 $x$ 的不等式 $2 x - 1 > k x + b$ 的解集是（）

A、 $x > 2$ B、 $x < 3$ C、 $x < 2$ D、 $x > 3$

查看试题解析
5. 如图，下列条件中能使 $▱ A B C D$ 成为菱形的是（）

A、 $A B = C D$ B、 $A C = B D$ C、 $∠ B A D = 90 °$ D、 $A B = B C$

查看试题解析
6. 在平面直角坐标系中，正比例函数 $y = k x (k \neq 0)$ 的图象经过第二、四象限，则函数 $y = k x - k$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
7. 数学课上，老师出示了如下图的一道证明题．
其中①②③分别填写（）

A、中线、 $D E ∥ A C$ 、一组对边平行且相等 B、中位线、 $D E ∥ A C$ 、两组对边分别相等 C、中线、 $C F = A D$ 、两组对边分别相等 D、中位线、 $D E ∥ A C$ 、一组对边平行且相等

查看试题解析
8. 嘉琪调查了本班每位同学对四类电视节目的喜爱情况，并绘制了不完整的扇形统计图1及条形统计图2（柱的高度从高到低排列）．条形统计图不小心被撕了一块，则图2中“（）”应填的电视节目是（）

A、体育 B、综艺 C、动画 D、新闻

查看试题解析
9. 如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（）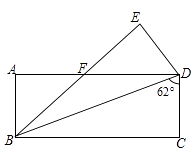

A、28° B、31° C、62° D、56°

查看试题解析
10. 关于函数 $y = 2 x - 1$ 的图象，下列说法正确的是（）

A、从左往右呈下降趋势 B、与 $y$ 轴的交点的坐标为 $(0 ， 1)$ C、可以由 $y = 2 x$ 的图象平移得到 D、当 $x > 0$ 时， $y > 0$

查看试题解析
11. 一个多边形边数每增加1条时，其内角和（）

A、增加 $180 °$ B、增加 $360 °$ C、不变 D、不能确定

查看试题解析
12. 如图，点 $A (3 ， 0)$ ， $B (0 ， 4)$ ，线段 $A B$ 绕点 $A$ 顺时针方向旋转 $90 °$ 得线段 $A C$ ，则点 $C$ 的坐标为（）

A、 $(7 ， 3)$ B、 $(6 ， 4)$ C、 $(8 ， 5)$ D、 $(8 ， 4)$

查看试题解析
13. 如图，正方形 $A B C D$ 中，点 $O$ 为对角线的交点，直线 $E F$ 过点 $O$ 分别交 $A B$ ， $C D$ 于 $E$ ， $F$ 两点（ $B E > E A$ ），若过点 $O$ 作直线与正方形的一组对边分别交于 $G$ ， $H$ 两点，满足 $G H = E F$ ，则这样的直线 $G H$ （不同于直线 $E F$ ）的条数共有（）

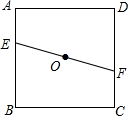A、1条 B、2条 C、3条 D、无数条

查看试题解析
14. 某加工厂要在5天内加工完220吨面粉，加工厂安排甲、乙两组共同完成加工任务．乙组加工中途停工一段时间维修设备，然后提高加工效率继续加工，直到与甲队同时完成加工任务为止．设甲、乙两组各自加工面粉数量 $y$ （吨）与甲组加工时间 $x$ （天）之间的关系如图所示，观察图象后，小李、小王分别说出各自的判断：
小李：甲组每天加工面粉20吨；
小王：到第3天结束时，甲、乙两组共完成总任务的一半．
下列说法正确的是（）

A、只有小李的判断正确 B、两人的判断都正确 C、只有小王的判断正确 D、两人的判断都错误

查看试题解析
15. 如图，在给定的△ABC中，动点D从点B出发沿BC方向向终点C运动，DE $∥$ AC交AB于点E，DF $∥$ AB交AC于点F，O是EF的中点，在整个运动过程中，△OBC的面积的大小变化情况是（）

A、不变 B、一直增大 C、先增大后减小 D、先减小后增大

查看试题解析
16. 图1，在 $R t △ A B C$ 中， $∠ A = 90 °$ ，点 $P$ 从点 $A$ 出发，沿三角形的边以 $1 c m$ /秒的速度逆时针运动一周，图2是点 $P$ 运动时，线段 $A P$ 的长度 $y (c m)$ 随运动时间 $x$ （秒）变化的关系图象，则图11－2中点 $Q$ 的纵坐标是（）

A、4.5 B、4.8 C、5 D、5.5

查看试题解析

二、填空题

17. 在函数 $y = \frac{x}{x - 5}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
18. 要想了解一本300页的书稿大约共有多少字，从中随机地选定一页作调查，数一数该页的字数．以下说法：①这本300页书稿的字数是总体；②每页书稿是个体；③从该书稿中选定的那一页的字数是总体的一个样本；④300是样本容量，其中正确的是．

查看试题解析
19. 如图1，菱形纸片 $A B C D$ 的面积为 $30 c m^{2}$ ，对角线 $A C$ 的长为 $6 c m$ ，将这个菱形纸片沿对角线剪开，得到四个全等的直角三角形，将这四个直角三角形按图2所示的方法拼成一个大正方形．则大正方形中空白小正方形的面积是 $c m^{2}$ ．

查看试题解析
20. 如图，把 $△ A B C$ 放在平面直角坐标系内，其中 $∠ C A B = 90 °$ ， $B C = 10$ ，点 $A$ ， $B$ 的坐标分别为 $(2 ， 0)$ ， $(8 ， 0)$ ．当直线 $y = 2 x + b$ （ $b$ 为常数）与 $△ A B C$ 有交点时，则 $b$ 的取值范围是．

查看试题解析

三、解答题

21. 如图，在 $△ A B C$ 中，三个顶点的坐标分别为 $A (0 ， - 2)$ ， $B (2 ， - 3)$ ， $C (4 ， 0)$ ．

(1)、将 $△ A B C$ 向左平移5个单位长度，再向上平移3个单位长度得到 $△ A^{'} B^{'} C^{'}$ ，直接写出 $△ A^{'} B^{'} C^{'}$ 的三个顶点坐标，并在图14的直角坐标系中画出 $△ A^{'} B^{'} C^{'}$ ；

(2)、设点 $P$ 在 $y$ 轴上，且 $△ A B P$ 与 $△ A B C$ 的面积相等，直接写出点 $P$ 的坐标．

查看试题解析
22. 学校开展了为期一周的“敬老爱亲”社会活动，为了解情况，学生会随机调查了部分学生在这次活动中做家务的时间，并将统计的时间（单位：小时）分成5组，A： $0.5 \leq x < 1$ ， B： $1 \leq x < 1.5$ ， C： $1.5 \leq x < 2$ ， D： $2 \leq x < 2.5$ ， E： $2.5 \leq x < 3$ ，制作了两幅如图的统计图．
请根据图中提供的信息，解答下列问题：

(1)、学生会随机调查了名学生；

(2)、补全频数分布直方图；

(3)、扇形E对应的圆心角为度；

(4)、若全校有1800名学生，估计该校在这次活动中做家务的时间不少于2小时的学生有多少人？

查看试题解析
23. 如图，直线 $l_{1}$ ： $y = - x - b$ 分别与 $x$ ， $y$ 轴交于 $A (6 ， 0)$ ， $B$ 两点，过点 $B$ 的直线 $l_{2}$ 交 $x$ 轴的负半轴于点 $C$ ，且 $O B ： O C = 3 ： 1$ ．

(1)、求点 $B$ ， $C$ 的坐标，并求直线 $B C$ 的函数表达式；

(2)、求 $S_{△ A O B} - S_{△ B O C}$ 的值；

(3)、若点 $P (m + 1 ， m - 1)$ 在 $△ A B C$ 的内部（包括边界），直接写出 $m$ 的取值范围．

查看试题解析
24. 某商店同时购进甲、乙两种商品共200件，其进价和售价如下表：
商品名称
甲
乙
进价（元/件）
80
90
售价（元/件）
100
120
设购进甲种商品 $x$ 件，该商场售完这200件商品获得的总利润为 $y$ 元．

(1)、求 $y$ 与 $x$ 的函数关系式（不写自变量 $x$ 的取值范围）；

(2)、该商店计划最多投入17000元用于购买这两种商品，至少要购进多少件甲商品？若售完这些商品，商店可获得的最大总利润是多少元？

查看试题解析
25. 如图，点 $E$ 是正方形 $A B C D$ 对角线 $A C$ 上一点，连接 $D E$ ，过点 $E$ 作 $E F ⊥ D E$ ，交射线 $B C$ 于点 $F$ ，以 $D E$ ， $E F$ 为邻边作矩形 $D E F G$ ，连接 $C G$ ．

(1)、求证：矩形 $D E F G$ 是正方形；

(2)、若 $A B = 4$ ， $C E = 3 \sqrt{2}$ ，求 $C G$ 的长度；

(3)、当线段 $D E$ 与正方形 $A B C D$ 的某条边的夹角是 $25 °$ 时，直接写出 $∠ E F C$ 的度数．

查看试题解析

商品名称	甲	乙
进价（元/件）	80	90
售价（元/件）	100	120