广东省肇庆市封开县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-19 类型:期末考试
一、单选题
-
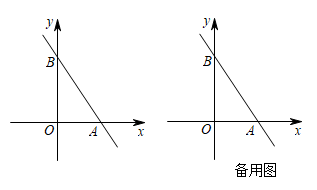
1. 下列根式中,最简二次根式的是( )A、 B、 C、 D、2. 下列三边组成的三角形中,不是直角三角形的是( )A、a=5,b=4,c=3 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 要使式子有意义,字母x的取值应满足( )A、 B、 C、 D、5. 一次函数的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 在第六届“创建全国文明城市”评选活动中,广东省有5个地级市上榜,它们的得分分别为:95,90,91,95,92,这组数据的中位数和众数分别是( )A、90,95 B、92,95 C、91,95 D、91,927. 如图,在四边形中,对角线、相交于点 , 下列条件不能判定这个四边形是平行四边形的是( )
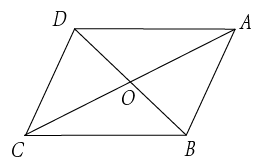 A、 , B、 , C、 , D、 ,8. 如图,在中, , , 分别以顶点、为圆心,大于的长为半径作圆弧,两条圆弧交于点、 , 作直线交边于点 . 若 , , 则的长是( )
A、 , B、 , C、 , D、 ,8. 如图,在中, , , 分别以顶点、为圆心,大于的长为半径作圆弧,两条圆弧交于点、 , 作直线交边于点 . 若 , , 则的长是( )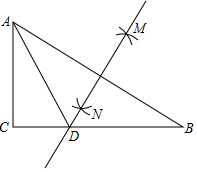 A、10 B、8 C、12 D、9. 两张全等的矩形纸片 , 按如图的方式叠放在一起, . 若 , , 则图中重叠(阴影)部分的面积为( )
A、10 B、8 C、12 D、9. 两张全等的矩形纸片 , 按如图的方式叠放在一起, . 若 , , 则图中重叠(阴影)部分的面积为( ) A、15 B、14 C、13 D、1210. 如图,四边形 ABCD 中,AB∥DC,AB=AD=BC=2,DC=4,动点 P 从点 A 出发, 在四边形的边上沿 A→B→C→D→A 的方向匀速运动,到点 A 停止,运动速度为每秒运动 1 个单位.设点 P 的运动路程为 x,在下列图象中,能表示△ABP 的面积 y 与 x 之间的变化关系的是( )
A、15 B、14 C、13 D、1210. 如图,四边形 ABCD 中,AB∥DC,AB=AD=BC=2,DC=4,动点 P 从点 A 出发, 在四边形的边上沿 A→B→C→D→A 的方向匀速运动,到点 A 停止,运动速度为每秒运动 1 个单位.设点 P 的运动路程为 x,在下列图象中,能表示△ABP 的面积 y 与 x 之间的变化关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 计算:( )2=。12. 如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA,OB的中点M,N,测得MN=16m,则A,B两点间的距离是m.
 13. 函数y=-2x+3的图象经过点(4,).14. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,CD=6,则AB= .
13. 函数y=-2x+3的图象经过点(4,).14. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,CD=6,则AB= . 15. 如图,中, , 分别以边向外作正方形,正方形的面积为36,正方形的面积为64,则正方形的边长是 .
15. 如图,中, , 分别以边向外作正方形,正方形的面积为36,正方形的面积为64,则正方形的边长是 . 16. 已知点 P(a,b)在一次函数 y=3x-1 的图象上,则 3a-b+1= .17. 如图,直线过正方形的顶点 , 点到直线的距离分别是和 , 且满足: , 则正方形的面积是 .
16. 已知点 P(a,b)在一次函数 y=3x-1 的图象上,则 3a-b+1= .17. 如图,直线过正方形的顶点 , 点到直线的距离分别是和 , 且满足: , 则正方形的面积是 .
三、解答题
-
18. 计算: .19. 已知正比例函数图象经过点(1)、求此正比例函数的解析式;(2)、当时,求x的取值范围.20. 湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.

求:
(1)、两棵景观树之间的距离;(2)、点B到直线AC的距离.21. 如图,四边形ABCD中,AD=BC,AE⊥BD,CF⊥BD,垂足分别是E、F,并且AE=CF.求证:四边形ABCD是平行四边形. 22. 为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:
22. 为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题: (1)、校团委随机调查的学生人数是 ▲ , 请你补全条形统计图;(2)、表示“50元”的扇形所占百分数是 ,(3)、求被调查的学生每人一周零花钱数额的平均数.
(1)、校团委随机调查的学生人数是 ▲ , 请你补全条形统计图;(2)、表示“50元”的扇形所占百分数是 ,(3)、求被调查的学生每人一周零花钱数额的平均数.