广东省湛江市廉江市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-19 类型:期末考试
一、单选题
-
1. 若二次根式有意义,则x的取值范围是( )A、 B、 C、 D、2. 对于圆的周长公式 , 下列说法正确的是( )A、是变量,2,是常量 B、是变量,是常量 C、是变量,是常量 D、 , 是变量,是常量3. 某校7名同学在“悦享冰雪,筑梦冬奥”绘画比赛活动中,成绩(单位:分)分别是86,88,90,90,92,95,97.这组数据的中位数和众数分别是( )A、88,90 B、90,90 C、95,90 D、90,924. 下列各组数据中,不能作为直角三角形边长的是( )A、 , , 2 B、5,7,11 C、9 ,12,15 D、15 ,20 ,255. 在下列给出的条件中,能判定四边形为平行四边形的是( )A、 B、 C、 D、6. 如图,在中,∠ACB=90°,D是边AB的中点,若AB=12,则CD的长是( )
 A、12 B、6 C、4 D、37. 某天早晨,小明从家骑自行车去上学,途中因自行车发生故障而维修,如图所示的图象反映了他骑车上学的整个过程,则下列结论正确的是( )
A、12 B、6 C、4 D、37. 某天早晨,小明从家骑自行车去上学,途中因自行车发生故障而维修,如图所示的图象反映了他骑车上学的整个过程,则下列结论正确的是( ) A、修车花了10分钟 B、小明家距离学校1000米 C、修好车后花了25分钟到达学校 D、修好车后骑行的速度是110米/分钟8. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、B、D的面积依次为6、10、24,则正方形C的面积为( )
A、修车花了10分钟 B、小明家距离学校1000米 C、修好车后花了25分钟到达学校 D、修好车后骑行的速度是110米/分钟8. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、B、D的面积依次为6、10、24,则正方形C的面积为( )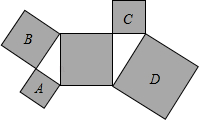 A、4 B、6 C、8 D、129. 在平面直角坐标系中,若点 , , 都在直线 上,则 , , 的大小关系是( )A、 B、 C、 D、10. 已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )
A、4 B、6 C、8 D、129. 在平面直角坐标系中,若点 , , 都在直线 上,则 , , 的大小关系是( )A、 B、 C、 D、10. 已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )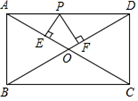 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 数据4,6,5,7,8的方差为 .12. 已知平行四边形中,比小40°,那么的度数是 .13. 如果y=+2,那么xy的值是 .14. 将一次函数的图象进行上下平移,使得平移之后的图象经过点 , 则平移之后图象的解析式为 .15. 若一个直角三角形的两边长分别是4cm,3cm,则第三条边长是 cm.16. 如图,平行四边形中,和的平分线交于E、F两点,则的长是 .
 17. 如图,平行四边形 中,对角线 相交于点 ,若 ,则图中阴影部分的面积是.
17. 如图,平行四边形 中,对角线 相交于点 ,若 ,则图中阴影部分的面积是.
三、解答题
-
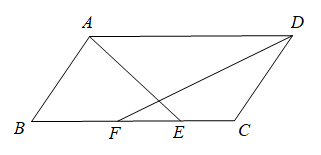
18. 计算:19. 已知y与x﹣1成正比例,且当x=3时,y=4(1)、求出y与x之间的函数解析式;(2)、当x=1时,求y的值.20. 如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明BE=DF.
 21. 如图,△ABC中,∠ACB=90°,AB=50,BC=30,CD⊥AB于D,求CD的长.
21. 如图,△ABC中,∠ACB=90°,AB=50,BC=30,CD⊥AB于D,求CD的长. 22. 表格是小明一学期数学成绩的记录,根据表格提供的信息回答下面的问题.
22. 表格是小明一学期数学成绩的记录,根据表格提供的信息回答下面的问题.考试类别
平时
期中考试
期末考试
第一单元
第二单元
第三单元
第四单元
成绩
88
92
90
86
90
96
 (1)、小明6次成绩的众数是分;中位数是分;(2)、计算小明平时成绩的方差;(3)、按照学校规定,本学期的综合成绩的权重如图所示,请你求出小明本学期的综合成绩,要写出解题过程.
(1)、小明6次成绩的众数是分;中位数是分;(2)、计算小明平时成绩的方差;(3)、按照学校规定,本学期的综合成绩的权重如图所示,请你求出小明本学期的综合成绩,要写出解题过程.(注意:①平时成绩用四次成绩的平均数;②每次考试满分都是100分).
23. 如图,在平面直角坐标系中,直线与轴交于 , 与轴交于 . (1)、求该直线的表达式和点的坐标;(2)、若轴一点 , 且 , 直接写出点的坐标.
(1)、求该直线的表达式和点的坐标;(2)、若轴一点 , 且 , 直接写出点的坐标.
