广东省云浮市新兴县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子是最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{4}$ C、 $\sqrt{8}$ D、 $\sqrt{0.5}$

查看试题解析
2. 某车间5名工人加工零件数依次为6，10，4，5，4，则这组数据的众数是（）

A、10 B、6 C、5 D、4

查看试题解析
3. 下列各组三条线段组成的三角形不是直角三角形的是（）

A、2，3，4 B、5，12，13 C、6，8，10 D、3，4，5

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $2 \sqrt{2} \times 3 \sqrt{2} = 5 \sqrt{2}$ D、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$

查看试题解析
5. 某校八年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小梅已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（）

A、平均数 B、众数 C、中位数 D、都可以

查看试题解析
6. 下列条件中能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $∠ A = ∠ B$ ， $∠ C = ∠ D$ B、 $A B = A D$ ， $C B = C D$ C、 $A B = C D$ ， $A D = B C$ D、 $A B // C D$ ， $A D = B C$

查看试题解析
7. 如图，菱形ABCD的两条对角线相交于点O，若AC=6，BD=4，则菱形ABCD的周长是（）

A、24 B、16 C、2 $\sqrt{3}$ D、4 $\sqrt{13}$

查看试题解析
8. 点 $(1 ， 5)$ 、 $(- 1 ， 1)$ 均在一次函数 $y = k x + b$ 的图象上，则k和b的值分别是（）

A、1，3 B、2，3 C、3，2 D、2，1

查看试题解析
9. 对于函数 $y = - 3 x + 6$ ，下列结论正确的是（）

A、它的图像必经过点 $(1 ， - 3)$ B、它的图象经过第一、二、三象限 C、当 $x > 2$ 时， $y < 0$ D、y的值随x值的增大而增大

查看试题解析
10. 如图，矩形ABCD中， $A B = 2$ ，点E在边AD上，EB平分∠AEC，∠DEC＝30°，则AE长为（）

A、1 B、 $4 - 2 \sqrt{3}$ C、 $2 \sqrt{2} - \sqrt{3}$ D、 $2 \sqrt{3} - 2$

查看试题解析

二、填空题

11. 某中学八年级人数相等的甲、乙两个班参加同一次数学测验，两班平均分和方差分别为 ${\bar{x}}_{甲} = 79$ 分， ${\bar{x}}_{乙} = 79$ 分， $S_{甲}^{2} = 201$ ， $S_{乙}^{2} = 235$ ，则成绩较为整齐的是班．（填“甲”或“乙”）

查看试题解析
12. 若代数式 $\sqrt{x - 3}$ 有意义，则实数x的取值范围是．

查看试题解析
13. 计算： $\sqrt{1 \frac{2}{3}} \div \sqrt{\frac{5}{6}} =$ ．

查看试题解析
14. 如图，点D、E、F分别是△ABC三边的中点，若△ABC的周长为12，则△DEF的周长为．

查看试题解析
15. 直角三角形两直角边长分别为5cm和12cm，则斜边上的中线长为cm．

查看试题解析
16. 若直线 $y = k x + 2$ 与两条坐标轴围成的三角形的面积是2，则k的值为．

查看试题解析
17. 如图，正方形ABCD边长为4，点P在对角线AC上（不含端点），以PA，PB为邻边作 $▱ P A Q B$ ，则对角线PQ长度的最小值为．

查看试题解析

三、解答题

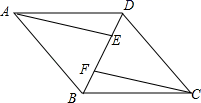
18. 化简：计算： $\sqrt{2} \times \sqrt{6} + (\sqrt{3} + 1) \times \sqrt{3}$

查看试题解析
19. 已知：如图，四边形ABCD是平行四边形，AE∥CF，且分别交对角线BD于点E，F．求证：AE＝CF．

查看试题解析
20. 如图，正方形网格的每个小方格都是边长为1的正方形，△ABC的顶点都在格点上.

(1)、分别求出AB，BC，AC的长；

(2)、试判断△ABC是什么三角形，并说明理由.

查看试题解析
21. 如图表示一轮船和一快艇沿相同的路线，从甲港到乙港行驶过程中路程随时间变化的图象（直线），根据图象解答下列问题：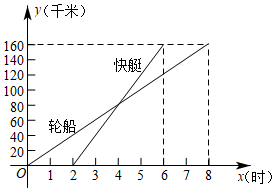

(1)、分别求出表示轮船和快艇行驶过程中的函数解析式；

(2)、问快艇出发多长时间赶上轮船？

(3)、轮船和快艇的行驶速度分别是多少？

查看试题解析
22. 四川雅安发生地震后，某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学会生随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：

(1)、本次接受随机抽样调查的学生人数为，图①中m的值是；

(2)、求本次调查获取的样本数据的平均数、众数和中位数；

(3)、根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

查看试题解析
23. 如图，将长方形ABCD沿AC对折，使△ABC落在△AEC的位置，且CE与AD相交于点F.

(1)、求证：EF=DF；

(2)、若AB= $\sqrt{3}$ ， BC=3，求折叠后的重叠部分(阴影部分)的面积.

查看试题解析
24. 如图，菱形ABCD的对角线交于点O，点E是菱形外一点，DE $∥$ AC，CE $∥$ BD．

(1)、求证：四边形DECO是矩形；

(2)、连接AE交BD于点F，当∠ADB＝30°，DE＝2时，求AF的长度．

查看试题解析
25. 在平面直角坐标系中，点A的坐标为 $(- 4 ， 0)$ ，点B在x轴上，直线 $y = - 2 x + a$ 经过点B，并与y轴交于点 $C (0 ， 7)$ ，直线AD与BC相交于点 $D (- 1 ， n)$ ；

(1)、求直线AD的解析式；

(2)、点P是线段BD上一点，过点P作 $P E ∥ A B$ 交AD于点E，若四边形AOPE为平行四边形，求E点坐标．

查看试题解析