广东省深圳市罗湖区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列关于防范“新冠肺炎”的标志中是轴对称图形，不是中心对称图形的是（）

A、戴口罩讲卫生 B、勤洗手勤通风 C、有症状早就医 D、少出门少聚集

查看试题解析
2. 若分式 $\frac{x^{2} - 9}{x + 3}$ 的值为0，则x的值为（）

A、4 B、-4 C、3或－3 D、3

查看试题解析
3. 正十二边形的每一个内角的度数为（）

A、120° B、135° C、150° D、108°

查看试题解析
4. 一元二次方程 $x^{2} - 6 x + 5 = 0$ 配方后可化为（）

A、 ${(x + 3)}^{2} = 14$ B、 ${(x - 3)}^{2} = - 4$ C、 ${(x + 3)}^{2} = - 14$ D、 ${(x - 3)}^{2} = 4$

查看试题解析
5. 在一个不透明的布袋中，红色、黑色、白色的小球共有50个，除颜色外其他完全相同，乐乐通过多次摸球试验后发现，摸到红色球、黑色球的频率分别稳定在27%和43%，则口袋中白色球的个数很可能是（）

A、15个 B、20个 C、25个 D、30个

查看试题解析
6. 多项式12ab³c＋8a³b的公因式是（　　）

A、4ab² B、4abc C、2ab² D、4ab

查看试题解析
7. 如图，平行四边形ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD＝12，则△DOE的周长为（）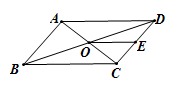

A、12 B、15 C、18 D、21

查看试题解析
8. 国家统计局统计数据显示，我国快递业务逐年增加，2019年至2021年我国快递业务收入由7500亿元增加到9000亿元．设我国2019年至2021年快递业务收入的年平均增长率为 $x$ ，则可列方程为（）

A、 $7500 (1 + 2 x) = 9000$ B、 $7500 \times 2 (1 + x) = 9000$ C、 $7500 {(1 + x)}^{2} = 9000$ D、 $7500 + 7500 (1 + x) + 7500 {(1 + x)}^{2} = 9000$

查看试题解析
9. 下列说法错误的是（）

A、对角线相等且互相垂直的平行四边形是正方形 B、对角线互相垂直的平行四边形是菱形 C、一组对边相等，另一组对边平行的四边形是平行四边形 D、对角线相等且互相平分的四边形是矩形

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为4，点 $E$ 在边 $C D$ 上，且 $C E = 1$ ，连结 $A E$ ，点 $F$ 在边 $A D$ 上，连结 $B F$ ，把 $△ A B F$ 沿 $B F$ 翻折，点 $A$ 恰好落在 $A E$ 上的点 $G$ 处，下列结论：① $A E = B F$ ；② $A D = 2 D F$ ；③ $S_{四边形 D F H E} = 6$ ；④ $G E = 0.2$ ，其中正确的有（）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解： $25 - x^{2} =$ ．

查看试题解析
12. 三角形两边的长分别为2和7，第三边的长是方程 $x^{2} - 10 x + 16 = 0$ 的根，则该三角形的周长为．

查看试题解析
13. 如图，菱形 $A B C D$ 中，若AC=10， $B D = 24$ ，则菱形 $A B C D$ 的面积为．

查看试题解析
14. 从3、5、6、9四个数中随机取一个数，不放回，再随机取一个数，把第一个数作为十位数字，第二个数作为个位数字，组成一个两位数，则这个两位数是奇数的概率是．

查看试题解析
15. 若关于x的方程 $\frac{1}{x - 4}$ + $\frac{m}{x + 4}$ = $\frac{m + 3}{x^{2} - 16}$ 无解，则m的值为．

查看试题解析

三、解答题

16. 解方程：

(1)、 $\frac{3}{x - 2} = \frac{1}{x}$ ．

(2)、 $\frac{1 - x}{x - 2} + 2 = \frac{1}{2 - x}$ ．

(3)、 $2 x^{2} - 4 x = 3$ ．

(4)、 $(4 x + 1)^{2} = \frac{16}{9}$ ．

查看试题解析
17. 先化简 $(x + 3 - \frac{7}{x - 3}) \div \frac{2 x^{2} - 8 x}{x - 3}$ ，再从 $0 \leq x \leq 4$ 中选一个适合的整数代入求值.

查看试题解析
18. $△ O A B$ 在平面直角坐标系中的位置如图所示．

(1)、将 $△ O A B$ 先向下平移4个单位，再向左平移1个单位得到 $△ O A_{1} B_{1}$ ，请写出移动后的点 $A_{1}$ 坐标， $B_{1}$ 坐标．

(2)、将 $△ O A B$ 绕着点 $O$ 顺时针方向旋转 $90 °$ 得到 $△ O A_{2} B_{2}$ ，画出 $△ O A_{2} B_{2}$ ．

查看试题解析
19. 在某次数学活动中，如图有两个可以自由转动的转盘A、B，转盘A被分成四个相同的扇形，分别标有数字1、2、3、4，转盘B被分成三个相同的扇形，分别标有数字5、6、7.若是固定不变，转动转盘（如果指针指在等分线上，那么重新转动，直至指针指在某个扇形区域内为止）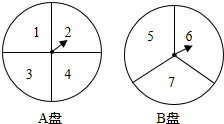

(1)、若单独自由转动A盘，当它停止时，指针指向偶数区的概率是.

(2)、小明自由转动A盘，小颖自由转动B盘，当两个转盘停止后，记下各个转盘指针所指区域内对应的数字，请用画树状图或列表法求所得两数之积为10的倍数的概率.

查看试题解析
20. 如图所示，在 $▱ A B C D$ 中，E，F分别为边 $A B$ ， $D C$ 的中点，连接 $E D$ ， $E C$ ， $E F$ ，作 $C G ∥ D E$ ，交 $E F$ 的延长线于点G，连接 $D G$ ．

(1)、求证：四边形 $D E C G$ 是平行四边形；

(2)、当 $E D$ 平分 $∠ A D C$ 时，求证：四边形 $D E C G$ 是矩形．

查看试题解析
21. 2022年2月4日，万众瞩目的冬奥会在我们的首都北京开幕了，与往届冬奥会所不同的是，这届冬奥会大家都被吉祥物—冰墩墩吸引了，导致市场大量缺货，为满足市场需求，温州某玩具加工厂打算紧急招聘70名工人进行冰墩墩的制作，已知冰墩墩分为普通款和升级款两种款式，普通工人每人每天可以生产2件普通款或1件升级款，根据市场行情，普通款每件利润为140元，升级款每件利润为350元，为保证全部售出，每生产1件升级款就将升级款的售价降低5元（每件利润不低于150元），设每天生产升级款 $x$ 件．

(1)、根据信息填表：
产品种类
每天工人数（人）
每天的产量（件）
每件可获得的利润（元）
普通款冰墩墩
升级款冰墩墩
$x$
$x$

(2)、当 $x$ 取多少时，工厂每日的利润可达到17200元？

查看试题解析
22. 如图，矩形 $A B C O$ 中，点 $C$ 在 $x$ 轴上，点 $A$ 在 $y$ 轴上，点 $B$ 的坐标是 $(- 6 ， 8)$ ．矩形 $A B C O$ 沿直线 $B D$ 折叠，使得点 $A$ 落在对角线 $O B$ 上的点 $E$ 处，折痕与 $O A$ 、 $x$ 轴分别交于点 $D$ 、 $F$ ．

(1)、求证： $△ B O F$ 是等腰三角形；

(2)、求直线 $B D$ 的解析式；

(3)、若点 $P$ 是平面内任意一点，点 $M$ 是线段 $B D$ 上的一个动点，过点 $M$ 作 $M N ⊥ x$ 轴，垂足为点 $N$ ．在点 $M$ 的运动过程中是否存在以 $P$ 、 $N$ 、 $E$ 、 $O$ 为顶点的四边形是菱形？若存在，直接写出点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析

产品种类	每天工人数（人）	每天的产量（件）	每件可获得的利润（元）
普通款冰墩墩
升级款冰墩墩	$x$	$x$