广东省深圳市宝安区2021-2022学年八年级下学期期末数学试题
试卷更新日期：2022-08-19 类型：期末考试
一、单选题
-
1. 若分式有意义，则x满足的条件是（ ）A、x≠2 B、x＝0 C、x≠0 D、x＝22. 下列四个图形中，是中心对称图形的是（ ）A、
B、
C、
D、
3. 下列各式由左到右的变形中，属于因式分解的是（ ）A、10x2﹣5x＝5x（2x﹣1） B、a（m＋n）＝am＋an C、（a＋b）2＝a2＋b2 D、x2﹣16＋6x＝（x＋4）（x﹣4）＋6x4. 若a＜b，则下列各式中一定成立的是（ ）A、﹣a＜﹣b B、ac＜bc C、a﹣1＜b﹣1 D、5. 如图，在ABCD中，对角线AC，BD相交于点O，若AC⊥AB，AC＝6，BD＝8，则AB的长为（ ）
A、10 B、 C、5 D、6. 把分式（x≠0，y≠0）中的分子、分母的x、y同时扩大为原来的2倍，那么分式的值（ ）A、扩大为原来的2倍 B、扩大为原来的4倍 C、缩小为原来的 D、不改变7. 下列命题中，错误的是（ ）A、经过平行四边形对角线交点的直线平分平行四边形的面积 B、过n边形的一个顶点，可以作（n﹣2）条对角线 C、斜边及一锐角分别相等的两个直角三角形全等 D、一组对边平行，一组对角相等的四边形是平行四边形8. 每年的6月5日为世界环境日．中国生态环境部将“共建清洁美丽世界”作为今年环境日的主题，旨在促进全社会增强生态环境保护意识，投身生态文明建设．某校学生会积极响应国家号召，组织七年级和八年级共100名同学参加环保活动，七年级学生平均每人收集15个废弃塑料瓶，八年级学生平均每人收集20个废弃塑料瓶．为了保证所收集的塑料瓶总数不少于1800个，至少需要多少名八年级学生参加活动？设参加活动的八年级学生x名，由题意得（ ）A、15x＋20（100﹣x）≥1800 B、15x＋20（100﹣x）＞1800 C、20x＋15（100﹣x）≥1800 D、20x＋15（100﹣x）≤18009. 如图，在▱ABCD中，以点C为圆心，适当长度为半径作弧，分别交CD、BC于点F、G，再分别以点F、G为圆心，大于长为半径作弧，两弧交于点H，作射线CH交AD于点E，连接BE，若DE＝5，AE＝3，BE＝4，则CE的长为（ ）
A、 B、 C、 D、810. 如图，在△ABC中，∠ABC＝45°，点D在AB上，点E在BC上，连接AE、CD、DE，若AE＝AC＝CD，CE＝4，则BD的长为（ ）
A、2 B、 C、4 D、二、填空题
-
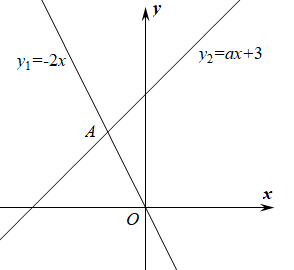
11. 因式分解：＝ ．12. 若一个n边形的每个内角都等于135°，则该n边形的边数是 ．13. 如图，函数y1＝﹣2x与y2＝ax+3的图象相交于点A(m，2)，则关于x的不等式﹣2x≤ax+3的解集是 ．
14. 如图，在△ABC中，∠ABC＝120°，点D为AC上一点，AD的垂直平分线交AB于点E，将△CBD沿着BD折叠，点C恰好和点E重合，则∠A的度数为 ．
15. 如图，在△ABC中，AB＝20，AC＝9，点M为BC的中点，AD平分△ABC的外角∠CAE，交BC延长线于点D，过点M作MN∥AD，交AB于点N，则AN的长为 ．
三、解答题
-
16. 解不等式组： ， 并把解集在数轴上表示出来．17. 先化简，再求值： ， 其中.18. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别为A（1，3），B（4，2），C（2，1）．
(1)、平移△ABC，使得点A的对应点A1的坐标为（﹣1，﹣1），则点C的对应点C1的坐标为；(2)、将△ABC绕原点旋转180°得到△A2B2C2 ， 在图中画出△A2B2C2；(3)、M、N为x轴上的两个动点，点M在点N的左侧，连接MN，若MN＝1，点D（0，﹣1）为y轴上的一点，连接DM、CN，则DM＋CN的最小值为 ．19. 5月11日，深圳市财政局披露数据显示，今年4月深圳市一般公共预算收入下滑约44%．为了扩大内需、促进消费、带动生产，深圳市商务局决定实施消费电子和家用电器购置补贴．星光商店计划购进A、B两种电器进行销售，已知每台B种电器的进价比每台A种电器的进价高1000元，该商店分别用10000元和40000元采购A、B两种电器，且采购的B种电器的数量是A种电器的两倍．(1)、求每台A、B种电器的进价分别为多少元？(2)、商店将A、B两种电器的售价分别定为1500元/台和3000元/台．在销售过程中，B种电器非常畅销，很快就销售一空．但A种电器的销售情况却不理想，在卖出a台后，商店决定进行促销活动，将剩余的A种电器按售价的8折出售，要使该商场卖完两种电器后获得的总利润不低于23200元，求a的最小值．20. 已知：如图，在四边形ABCD中，DE⊥AC，BF⊥AC，垂足分别为E，F，延长DE、BF，分别交AB于点H，交BC于点G，若AD∥BC，AE＝CF．
(1)、求证：四边形ABCD为平行四边形；(2)、若∠DAH＝∠GBA，GF＝2，CF＝4，求AD的长．21. 入夏以来，居民用电量持续攀升．为鼓励居民节约用电，某市从6月起，启用夏季收费政策，该政策有两种用电收费方法：分时电表
普通电表
峰时（9：00﹣22：00）
谷时（22：00到次日9：00）
电价0.62元/kW•h
电价0.82元/kW•h
电价0.42元/kW•h
小亮所在数学学习小组提出以下问题：家庭使用分时电表是不是一定比普通电表合算呢？他们进行了以下研究：
(1)、设某家庭某月用电总量akW•h（a为常数），其中峰时用电xkW•h，用分时电表计价时总价为y1元，普通计价时总价为y2元．求出y1、y2与用电量之间的关系式；(2)、请判断使用分时电表是不是一定比普通电表更合算？(3)、小亮家所在小区的电表今年已经全部换成分时电表．若小亮家6月份用电250kW•h，其中峰时用电100kW•h，试用（2）中的结论，分析小亮家使用分时电表是否合算．22. 如图1，在平面直角坐标系中，△ABO为直角三角形，∠ABO＝90°，∠AOB＝30°，OB＝3，点C为OB上一动点．
(1)、点A的坐标为；(2)、连接AC，并延长交y轴于点D，若△OAD的面积恰好被x轴分成1∶2两部分，求点C的坐标；(3)、如图2，若∠OAC＝30°，将△OAB绕点O顺时针旋转，得到△OA'B'，如图2所示，OA'所在直线交直线AC于点P，当△OAP为直角三角形时，直接写出点的坐标．