广东省汕尾市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-19 类型:期末考试
一、单选题
-
1. 下列实数中,最大的数是( )A、 B、 C、 D、2. 2022年北京打造了一届绿色环保的冬奥会.张家口赛区按照“渗、滞、蓄、净、用、排”的原则,在古杨树场馆群修建了250000立方米雨水收集池,用于收集雨水和融雪水,最大限度减少水资源浪费.将250000用科学记数法表示应为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下列三个长度的线段能组成直角三角形的是( )A、1, , B、1, , C、2,4,6 D、5,5,65. 一次函数y=2x+4的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积( )
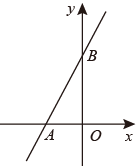 A、6 B、8 C、2 D、46. “五一”假期,小萌一家计划自驾车去某地踏青,手机导航系统推荐了两条线路,线路一全程120 , 线路二全程144 , 汽车在线路二上行驶的平均时速是线路一上时速的1.8倍,线路二的用时预计比线路一少40分钟,如果设汽车在线路一上行驶的平均速度为 , 则下列所列方程正确的是( )A、 B、 C、 D、7. 为了了解班级同学的家庭用水情况,小明在全班50名同学中,随机调查了10名同学家庭中一年的月平均用水量(单位:吨),绘制了条形统计图如图所示.这10名同学家庭中一年的月平均用水量的中位数是( )
A、6 B、8 C、2 D、46. “五一”假期,小萌一家计划自驾车去某地踏青,手机导航系统推荐了两条线路,线路一全程120 , 线路二全程144 , 汽车在线路二上行驶的平均时速是线路一上时速的1.8倍,线路二的用时预计比线路一少40分钟,如果设汽车在线路一上行驶的平均速度为 , 则下列所列方程正确的是( )A、 B、 C、 D、7. 为了了解班级同学的家庭用水情况,小明在全班50名同学中,随机调查了10名同学家庭中一年的月平均用水量(单位:吨),绘制了条形统计图如图所示.这10名同学家庭中一年的月平均用水量的中位数是( ) A、7.5 B、7 C、6.5 D、68. 如图,平行四边形ABCD的对角线交于点O,且AB≠AD,过O作OE⊥BD交BD于点E.若△CDE的周长为10,则平行四边形ABCD的周长为( )
A、7.5 B、7 C、6.5 D、68. 如图,平行四边形ABCD的对角线交于点O,且AB≠AD,过O作OE⊥BD交BD于点E.若△CDE的周长为10,则平行四边形ABCD的周长为( ) A、10 B、16 C、18 D、209. 如果 ,那么代数式 的值为( )A、 B、 C、 D、10. 一次函数y1=ax+b与y2=cx+d的图像如图所示,下列结论中正确的有( )
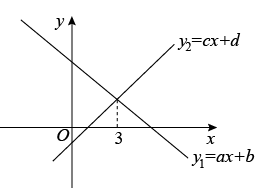
A、10 B、16 C、18 D、209. 如果 ,那么代数式 的值为( )A、 B、 C、 D、10. 一次函数y1=ax+b与y2=cx+d的图像如图所示,下列结论中正确的有( )①对于函数y=ax+b来说,y随x的增大而减小②函数y=ax+d的图像不经过第一象限③④
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若二次根式在实数范围内有意义,则的取值范围是 .12. 因式分解: .13. 已知 ,那么 的值是14. 如图的平面图形由多条线段首尾相连构成,已知∠A=90°,则∠D+∠E+∠F+∠G= .
 15. 如图,在中, , , , , 分别为 , , 的中点,若 , 则的长度为 .
15. 如图,在中, , , , , 分别为 , , 的中点,若 , 则的长度为 . 16. 在平面直角坐标系中,直线l:y=x+1与y轴交于点A1 , 如图所示,依次作正方形OA1B1C1 , 正方形C1A2B2C2 , 正方形C2A3B3C3 , 正方形C3A4B4C4 , 点A1 , A2 , A3 , A4 , …在直线l上,点C1 , C2 , C3 , C4 , …在x轴正半轴上,则A4的坐标是;的坐标是 .
16. 在平面直角坐标系中,直线l:y=x+1与y轴交于点A1 , 如图所示,依次作正方形OA1B1C1 , 正方形C1A2B2C2 , 正方形C2A3B3C3 , 正方形C3A4B4C4 , 点A1 , A2 , A3 , A4 , …在直线l上,点C1 , C2 , C3 , C4 , …在x轴正半轴上,则A4的坐标是;的坐标是 . 17. 如图,在矩形中, , , 点 , 分别是 , 边上的动点,且 , 点为的中点,点为上的一动点,则的最小值为 .
17. 如图,在矩形中, , , 点 , 分别是 , 边上的动点,且 , 点为的中点,点为上的一动点,则的最小值为 .
三、解答题
-
18. 计算: .19. 解不等式组: .20. 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.
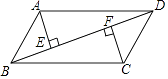 21. 如图,在中, , 为边上一点,且 .
21. 如图,在中, , 为边上一点,且 . (1)、作∠的角平分线 , 与交于点(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接 , 若 , 求∠的度数.22. 我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查名学生在某一周主题阅读文章的篇数,并制成统计图表.
(1)、作∠的角平分线 , 与交于点(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接 , 若 , 求∠的度数.22. 我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查名学生在某一周主题阅读文章的篇数,并制成统计图表.文章阅读的篇数(篇)
3
4
5
6
7及以上
人数(人)
20
28
16
12
某校抽查的学生文章阅读的篇数统计表

请根据统计图表中的信息,解答下列问题:
(1)、 , ;(2)、图中“3篇”部分的圆心角的大小是度;(3)、若该校共有800名学生,根据抽查结果,估计该校学生在这一周内文章阅读的篇数为4篇的人数.23. 如图,四边形是矩形,点、分别在边、上,将矩形沿对折,点与点恰好重合. (1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.24. 某校运动会需购买、两种奖品.若购买种奖品3件和种奖品2件,共需60元;若购买种奖品5件和种关品3件,共需95元.(1)、求、两种奖品单价各是多少元?(2)、学校计划购买、两种奖品共100件,购买费用不超过1150元,且种奖品的数量不大于种奖品数量的3倍.设购买种奖品件,购买费用为元,写出(元)与(件)之间的函数表达式,并求最少费用的值.25. 如图,在平面直角坐标系中,直线l:y=-x+5与y轴交于点A,直线l:y=kx+b与x轴、y轴分别交于点B(-4,0)和点C,直线l1与直线l2交于点D(2,m).
(1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.24. 某校运动会需购买、两种奖品.若购买种奖品3件和种奖品2件,共需60元;若购买种奖品5件和种关品3件,共需95元.(1)、求、两种奖品单价各是多少元?(2)、学校计划购买、两种奖品共100件,购买费用不超过1150元,且种奖品的数量不大于种奖品数量的3倍.设购买种奖品件,购买费用为元,写出(元)与(件)之间的函数表达式,并求最少费用的值.25. 如图,在平面直角坐标系中,直线l:y=-x+5与y轴交于点A,直线l:y=kx+b与x轴、y轴分别交于点B(-4,0)和点C,直线l1与直线l2交于点D(2,m).

 (1)、求直线l2的解析式;(2)、若点E为线段BC上一个动点,过点E作EF⊥x轴,垂足为F,且与直线交于点G,当EG=6时,求点G的坐标;(3)、问在平面上是否存在点H,使得以点A,C,D,H为顶点的四边形是平行四边形,若存在,直接写出所有满足条件的点H的坐标;若不存在,请说明理由.
(1)、求直线l2的解析式;(2)、若点E为线段BC上一个动点,过点E作EF⊥x轴,垂足为F,且与直线交于点G,当EG=6时,求点G的坐标;(3)、问在平面上是否存在点H,使得以点A,C,D,H为顶点的四边形是平行四边形,若存在,直接写出所有满足条件的点H的坐标;若不存在,请说明理由.