广东省茂名市高州市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-19 类型:期末考试
一、单选题
-
1. 二次根式 中 的取值范围是( )A、 B、 且 C、 D、 且2. 下列图形中既是中心对称图形,又是轴对称图形是( )
 A、圆 B、平行四边形 C、等边三角形 D、等腰直角三角形3. 如下图,在等腰直角ABC中,∠B=90°,将ABC绕顶点A逆时针方向旋转60°后得到AB’C’,则∠BAC’等于( )
A、圆 B、平行四边形 C、等边三角形 D、等腰直角三角形3. 如下图,在等腰直角ABC中,∠B=90°,将ABC绕顶点A逆时针方向旋转60°后得到AB’C’,则∠BAC’等于( ) A、60° B、105° C、120° D、135°4. 若关于的不等式的解集如图所示,则m等于( )
A、60° B、105° C、120° D、135°4. 若关于的不等式的解集如图所示,则m等于( ) A、0 B、1 C、2 D、35. 如图,平分 , 于点 , , 点是射线上的任意一点,则的最小值是( )
A、0 B、1 C、2 D、35. 如图,平分 , 于点 , , 点是射线上的任意一点,则的最小值是( ) A、6 B、5 C、4 D、36. 若 ,则下列结论中,不一定成立的是( )A、 B、 C、 D、7. 多项式2x2﹣2y2分解因式的结果是( )A、2(x+y)2 B、2(x﹣y)2 C、2(x+y)(x﹣y) D、2(y+x)(y﹣x)8. 炎炎夏日,甲安装队为A小区安装60台空调,乙安装队为B小区安装50台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台.设乙队每天安装x台,根据题意,下面所列方程中正确的是( )A、 B、 C、 D、9. 如图,在△ABC中,∠C=90°,E是CA延长线上一点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF,BE,AB的中点,则PQ的长为( )
A、6 B、5 C、4 D、36. 若 ,则下列结论中,不一定成立的是( )A、 B、 C、 D、7. 多项式2x2﹣2y2分解因式的结果是( )A、2(x+y)2 B、2(x﹣y)2 C、2(x+y)(x﹣y) D、2(y+x)(y﹣x)8. 炎炎夏日,甲安装队为A小区安装60台空调,乙安装队为B小区安装50台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台.设乙队每天安装x台,根据题意,下面所列方程中正确的是( )A、 B、 C、 D、9. 如图,在△ABC中,∠C=90°,E是CA延长线上一点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF,BE,AB的中点,则PQ的长为( ) A、2 B、4 C、6 D、310. 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°.
A、2 B、4 C、6 D、310. 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°.①四边形ACED是平行四边形;②△BCE是等腰三角形;③四边形ACEB的周长是 ;④四边形ACEB的面积是16.则以上结论正确的是( )
 A、①② B、②④ C、①②③ D、①③④
A、①② B、②④ C、①②③ D、①③④二、填空题
-
11. 关于x的方程有增根,则a的值是 .12. 如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.
 13. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是
13. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 14. 运行程序如图所示,从“输入实数x”到“结果是否>18”为一次程序操作,若输入x后程序操作进行了两次停止,则x的取值范围是.
14. 运行程序如图所示,从“输入实数x”到“结果是否>18”为一次程序操作,若输入x后程序操作进行了两次停止,则x的取值范围是. 15. 如图,在中, , 将绕点按逆时针方向旋转后得到 , 则阴影部分面积为 .
15. 如图,在中, , 将绕点按逆时针方向旋转后得到 , 则阴影部分面积为 . 16. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
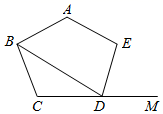
16. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .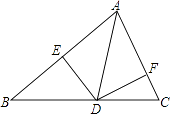 17. 如图,已知△ABC(AB > AC)中,∠BAC = 60°,AC = 4,D为BC边上的中点,过点D的直线DF将△ABC的周长平分且交AB于点F,则DF的长为 .
17. 如图,已知△ABC(AB > AC)中,∠BAC = 60°,AC = 4,D为BC边上的中点,过点D的直线DF将△ABC的周长平分且交AB于点F,则DF的长为 .
三、解答题
-
18. 解不等式组 .19.(1)、对于任意不相等的两个实数a、b,定义运算※如下:a※b= ,例如3※2= = ,求8※12的值.(2)、先化简,再求值: + ÷ ,其中a=1+ .20. 在平面直角坐标系中的位置如图所示.

⑴作关于点成中心对称的 .
⑵将向右平移3个单位,作出平移后的 .
⑶在轴上求作一点 , 使的值最小,并求出点的坐标.
21. 已知:如图,中, , 且于交的延长线于.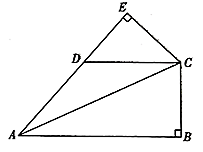 (1)、求证:(2)、如果连接 , 请写出与的关系并证明22. 中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化.2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开晋商又以“万里茶道”著称.晋商古街某茶店用4000元购进了A种茶叶若干盒,又用8400元购进B种茶叶若干盒,若所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍;(1)、A,B两种茶叶每盒进价分别为多少元?(2)、第一次所购茶叶全部售完后,第二次购进A、B两种茶叶共100盒,(A、B进价不变,A种茶叶不少于20盒),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元,怎样进货才能获得最大利润?23. 定义运算 min{a,b}:当 a≥b 时,min{a,b}=b;当 a<b 时,min{a,b}=a;如:min{4,0}=0;min{2,2}=2;min{﹣3,﹣1}=﹣3.根据该定义运算完成下列问题:
(1)、求证:(2)、如果连接 , 请写出与的关系并证明22. 中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化.2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开晋商又以“万里茶道”著称.晋商古街某茶店用4000元购进了A种茶叶若干盒,又用8400元购进B种茶叶若干盒,若所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍;(1)、A,B两种茶叶每盒进价分别为多少元?(2)、第一次所购茶叶全部售完后,第二次购进A、B两种茶叶共100盒,(A、B进价不变,A种茶叶不少于20盒),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元,怎样进货才能获得最大利润?23. 定义运算 min{a,b}:当 a≥b 时,min{a,b}=b;当 a<b 时,min{a,b}=a;如:min{4,0}=0;min{2,2}=2;min{﹣3,﹣1}=﹣3.根据该定义运算完成下列问题: (1)、min{﹣3,2}= , 当 x≤3 时,min{x,3}=;(2)、如图,已知直线 y1=x+m 与 y2=kx﹣2 相交于点 P(﹣2,1),若 min{x+m,kx﹣2}=kx﹣2,结合图象,直接写出 x 的取值范围是;(3)、若 min{3x﹣1,﹣x+3}=3﹣x,求 x 的取值范围.24. 如图,点E为▱ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF.
(1)、min{﹣3,2}= , 当 x≤3 时,min{x,3}=;(2)、如图,已知直线 y1=x+m 与 y2=kx﹣2 相交于点 P(﹣2,1),若 min{x+m,kx﹣2}=kx﹣2,结合图象,直接写出 x 的取值范围是;(3)、若 min{3x﹣1,﹣x+3}=3﹣x,求 x 的取值范围.24. 如图,点E为▱ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF. (1)、若∠BAE=65°,∠DEC=40°,求∠ECD的度数;(2)、求证:四边形AFHD为平行四边形;(3)、连接EH,交BC于点O,若OC=OH,求证: .25. 如图,在平面直角坐标系中,四边形各顶点坐标分别为 , , , .
(1)、若∠BAE=65°,∠DEC=40°,求∠ECD的度数;(2)、求证:四边形AFHD为平行四边形;(3)、连接EH,交BC于点O,若OC=OH,求证: .25. 如图,在平面直角坐标系中,四边形各顶点坐标分别为 , , , . (1)、求所在直线的函数表达式;(2)、若直线上有一点 , 使得与的面积相等,求出点的坐标;(3)、有一动点从点出发,沿折线运动,速度为1单位长度/秒,运动时间为秒,到达点时停止运动.试求出的面积关于的函数关系式,并写出相应的取值范围.
(1)、求所在直线的函数表达式;(2)、若直线上有一点 , 使得与的面积相等,求出点的坐标;(3)、有一动点从点出发,沿折线运动,速度为1单位长度/秒,运动时间为秒,到达点时停止运动.试求出的面积关于的函数关系式,并写出相应的取值范围.