广东省河源市和平县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $a < b$ ，下列四个不等式中错误的是（）

A、 $2 - a < 2 - b$ B、 $3 a < 3 b$ C、 $- 3 a > - 3 b$ D、 $a + 3 < b + 3$

查看试题解析
2. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”，其中既是中心对称又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，AD是∠BAC的角平分线，点P在AD上， $P M ⊥ A B$ 于点M， $P M = 3$ ，则点P到AC的距离是（）

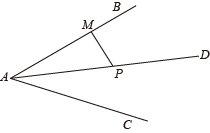A、1 B、2 C、3 D、4

查看试题解析
4. 四边形ABCD中，对角线AC、BD交于点O，能判断四边形ABCD是平行四边形的是（）

A、AB $∥$ CD，AD＝BC B、∠A＝∠B，∠C＝∠D C、AB＝AD，CB＝CD D、AO＝CO，BO＝DO

查看试题解析
5. 不等式组 ${\begin{array}{l} 2 - x > 1 \\ 2 x \leq x + 4 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 化简 $\frac{x^{2} - 1}{2 x} \div \frac{x - 1}{x}$ 的结果是（）

A、 $x - 1$ B、 $x + 1$ C、 $\frac{2}{x - 1}$ D、 $\frac{x + 1}{2}$

查看试题解析
7. 如图，在平行四边形 $A B C D$ 中，对角线 $A C ， B D$ 交于点O，P是 $A B$ 的中点.若 $O P = 4$ ， $A P = 3$ ，则平行四边形 $A B C D$ 的周长为（）

A、12 B、14 C、22 D、28

查看试题解析
8. 如图，在 $▱ A B C D$ 中， $∠ A B C$ ， $∠ B C D$ 的平分线分别交 $A D$ 于点E，F，若 $A B = 3$ ， $A D = 4$ ，则EF的长是（）

A、2 B、2.5 C、3 D、3.5

查看试题解析
9. 直线 $l_{1}$ ： $y = k_{1} x + b$ 与直线 $l_{2}$ ： $y = k_{2} x$ 在同一平面直角坐标系的图象如图所示，则关于 $x$ 的不等式 $k_{1} x + b < k_{2} x$ 的解集为（）

A、 $x < - 1$ B、 $x > - 1$ C、 $x < - 2$ D、 $x > - 2$

查看试题解析
10. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = 3$ ， $A C = 4$ ，将 $△ A B C$ 绕点B逆时针旋转得 $△ A^{'} B C^{'}$ ，若点 $C^{'}$ 在 $A B$ 上，连接 $C C^{'}$ ，则 $C C^{'}$ 的长为（）

A、 $\frac{7 \sqrt{5}}{6}$ B、 $\frac{5 \sqrt{5}}{6}$ C、 $\frac{6 \sqrt{5}}{5}$ D、 $\frac{3 \sqrt{5}}{5}$

查看试题解析

二、填空题

11. 因式分解： $x^{3} y - 9 x y =$ ．

查看试题解析
12. 一个多边形的内角和是720°，那么这个多边形是边形．

查看试题解析
13. 当式子 $\frac{2 x}{x - 2}$ 有意义时，实数 $x$ 的取值范围是．

查看试题解析
14. 已知 $m + n = 4$ ， $m n = - 5$ ，则 $m^{2} n + m n^{2} =$ ．

查看试题解析
15. 如图，将三角形ABC沿水平方向向左平移到三角形DEF的位置．已知点A，D之间的距离为3，CE＝12，则BF的长是．

查看试题解析
16. 如图，已知 $∠ B A C = 60 °$ ， AD是∠BAC的角平分线且 $A D = 8$ ，作AD的垂直平分线交AC于点F，作 $D E ⊥ A C$ ，连接DF，则△DEF周长为．

查看试题解析
17. 如图，EF过 $▱ A B C D$ 对角线的交点O，交AD于点E，交BC于点F．则① $O E = O F$ ；②若 $A B = 4$ ， $A C = 6$ ，则 $2 < B D < 14$ ；③图中共有4对全等三角形；④ $S_{四边形 A B F E} = S_{△ A B C}$ ．其中正确结论有个．

查看试题解析

三、解答题

18. 解分式方程： $\frac{3 x}{x - 1} + \frac{2}{x - 1} = 1$ ．

查看试题解析
19. 先化简，再求值 $(\frac{x}{x - 2} - 1) \div \frac{x^{2} + 4 x + 4}{x^{2} - 4}$ ，其中x＝3．

查看试题解析
20. 如图，在平面直角坐标系中，已知网格的每个小正方形的边长均为1个单位长度， $△ A B C$ 的三个顶点的坐标分别为 $A (- 1 ， 2) ， B (- 4 ， 1) ， C (- 3 ， - 1)$ ．

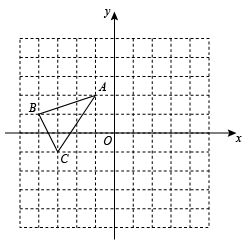(1)、将 $△ A B C$ 先向右平移2个单位长度，再向下平移3个单位长度后得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ 并写出点B的对应点 $B_{1}$ 的坐标；

(2)、画出 $△ A_{1} B_{1} C_{1}$ 绕点 $A_{1}$ 按逆时针方向旋转 $90 °$ 的 $△ A_{1} B_{2} C_{2}$ ，并写出点 $C_{1}$ 的对应点 $C_{2}$ 的坐标．

查看试题解析
21. 某单位计划在新年期间组织员工到某地旅游，参加旅游的人数估计为10至25人，甲、乙两家旅行社的服务质量相同，且报价都是每人200元．经过协商，甲旅行社表示可给予每位游客七五折优惠；乙旅行社表示可先免去一位游客的旅游费用，然后给予其余游客八折优惠．设该单位参加这次旅游的人数是x人，选择甲旅行社时，所需的费用为 $y_{1}$ 元；选择乙旅行社时，所需的费用为 $y_{2}$ 元．

(1)、请分别写出 $y_{1}$ ， $y_{2}$ 与x之间关系式；

(2)、该单位选择哪一家旅行社支付的旅游费用较少？

查看试题解析
22. 如图，在等边三角形ABC中，点D，E分别在边BC、AC上，若 $C D = 3$ ， $D E ∥ A B$ ，过点E作 $E F ⊥ D E$ ，交BC的延长线于点F．

(1)、求证： $△ C D E$ 为等边三角形；

(2)、求EF的长．

查看试题解析
23. 为美化小区环境，物业计划安排甲、乙两个工程队完成小区绿化工作.已知甲工程队每天绿化面积是乙工程队每天绿化面积的2倍，甲工程队单独完成600m²的绿化面积比乙工程队单独完成600m²的绿化面积少用2天.

(1)、求甲、乙两工程队每天绿化的面积分别是多少m²；

(2)、小区需要绿化的面积为9600m² ，物业需付给甲工程队每天绿化费为0.3万元，付给乙工程队每天绿化费为0.2万元，若要使这次的绿化总费用不超过12万元，则至少应安排甲工程队工作多少天？

查看试题解析
24. 如图，在 $△ A B C$ 中， $A C = B C$ ，点F为AB的中点，边AC的垂直平分线交AC、CF、CB于点D、O、E，连接OA、OB．

(1)、求证： $△ O B C$ 为等腰三角形；

(2)、若 $∠ A C F = 23 °$ ，求 $∠ B O E$ 的度数；

(3)、若 $A B = 10$ ， $C F = 25$ ，求线段OA的长．

查看试题解析
25. 如图，点E为 $▱ A B C D$ 的边AD上的一点，连接EB并延长，使 $B F = B E$ ，连接EC并延长，使 $C G = C E$ ，连接FG．H为FG的中点，连接DH，AF．

(1)、若 $∠ B A E = 70 °$ ， $∠ D C E = 20 °$ ，求 $∠ D E C$ 的度数；

(2)、求证：四边形AFHD为平行四边形；

(3)、连接EH，交BC于点O，若 $O C = O H$ ，求证： $O E = \frac{1}{2} B C$ ．

查看试题解析