福建省福州市五校联考2022届高三上学期数学期中考试试卷
试卷更新日期:2022-08-18 类型:期中考试
一、单选题
-
1. 已知命题 , 则为( )A、 B、 C、 D、2. 已知集合 ,则如图所示阴影部分表示的集合为( )
 A、 B、 C、 D、3. 已知 为虚数单位,且复数 满足 ,则 的共轭复数是( )A、 B、 C、 D、4. 若 ,则( )A、 B、 C、 D、5. 在△ 中, 为 边上的中线,E为 的中点,则 ( )A、 B、 C、 D、6. 函数 在其定义域上的图象大致为( )A、
A、 B、 C、 D、3. 已知 为虚数单位,且复数 满足 ,则 的共轭复数是( )A、 B、 C、 D、4. 若 ,则( )A、 B、 C、 D、5. 在△ 中, 为 边上的中线,E为 的中点,则 ( )A、 B、 C、 D、6. 函数 在其定义域上的图象大致为( )A、 B、
B、 C、
C、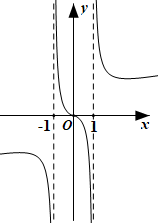 D、
D、 7. 标准对数远视力表(如图)采用的“五分记录法”是我国独创的视力记录方式,此表中各行均为正方形“E”形视标,且从视力5.2的视标所在行开始往上,每一行“E”的边长都是下方一行“E”边长的 倍,若视力4.2的视标边长为 ,则视力5.1的视标边长为( )
7. 标准对数远视力表(如图)采用的“五分记录法”是我国独创的视力记录方式,此表中各行均为正方形“E”形视标,且从视力5.2的视标所在行开始往上,每一行“E”的边长都是下方一行“E”边长的 倍,若视力4.2的视标边长为 ,则视力5.1的视标边长为( ) A、 B、 C、 D、8. 定义在R上的偶函数在上单调递减,且满足 , , , 则不等式组的解集为( )A、 B、 C、 D、
A、 B、 C、 D、8. 定义在R上的偶函数在上单调递减,且满足 , , , 则不等式组的解集为( )A、 B、 C、 D、二、多选题
-
9. 已知向量 , , , 设的夹角为 , 则( )A、 B、 C、 D、10. 对于实数a、b、c,下列命题中正确的是( )A、若 , 则 B、若 , , 则 , C、若 , 则 D、若 , 则11. 已知复数(其中i为虚数单位),下列说法正确的是( )A、复数z在复平面上对应的点可能落在第二象限 B、 C、 D、为实数12. 已知函数 是定义在R上的奇函数,当 时, ,给出下列命题:①当 时, ;②函数 有2个零点;③ 的解集为 ;④ ,都有 .其中所有正确结论的编号是( )A、① B、② C、③ D、④
三、填空题
-
13. 已知且 , 则.14. 曲线C:在点M(1,e)处的切线方程为 .15. 已知向量 , 满足 , , ,则 与 的夹角为 .16. 已知定义域为的函数满足 , , 其中为的导函数,则不等式的解集为.
四、解答题
-
17. 已知p: ,q:x>a2-2a-1(1)、若 为真,求 的取值范围;(2)、若 是 的充分不必要条件,求实数 的取值范围.18. 如图,以为始边作角与 , 它们的终边分别与单位圆相交于点、 , 已知点的坐标为 .
 (1)、求的值;(2)、已知 , 求 .19. 在① , ② , ③这三个条件中任选一个,补充在下面的问题中,并解答.
(1)、求的值;(2)、已知 , 求 .19. 在① , ② , ③这三个条件中任选一个,补充在下面的问题中,并解答.问题:设是数列的前n项和,且 , _______,求的通项公式,并判断是否存在最大值,若存在,求出最大值;若不存在,说明理由.