陕西省渭南市华州区2021-2022学年七年级下学期期末教学质量检测数学试卷

试卷更新日期：2022-08-18 类型：期末考试

进入出卷网下载

一、选择题(共8小题,每小题3分,计24分.)

1. 在 $△ A B C$ 中，如果 $∠ A = 60^{\circ} ， ∠ B = 45^{\circ}$ ，那么 $∠ C$ 等于（）

A、 $115^{\circ}$ B、 $105^{\circ}$ C、 $75^{\circ}$ D、 $45^{\circ}$

查看试题解析
2. 自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识.下面是科学防控知识的图片，图片上有图案和文字说明，其中图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列事件中，随机事件是（）

A、购买一张福利彩票中奖了 B、通常水加热到 $100 ^{\circ} C$ 时会沸腾 C、在地球上，抛出的篮球会下落 D、郑一枚㳙子，向上一面的字数一定大于零

查看试题解析
4. 下列句子是命题的是（）

A、画两条相等的线段. B、等于同一个角的两个角相等吗? C、延长线段 $A O$ 到 $C$ ，使 $O C = O A$ . D、两直线平行，内错角相等.

查看试题解析
5. 若 $a > 0$ 且 $a^{x} = 2 ， a^{y} = 3$ ，则 $a^{x - 2 y}$ 的值为（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{2}{9}$

查看试题解析
6. 小明有两根长度分别为5cm和8cm的木棒，他想钉一个三角形的木框.现有5根木棒供他选择，其长度分别为 $3 cm 、 5 cm 、 10 cm 、 13 cm 、 14 cm$ .小明随手拿了一根，恰好能够组成一个三角形的概率为（）

A、 $\frac{2}{5}$ B、 $\frac{1}{2}$ C、 $\frac{3}{5}$ D、1

查看试题解析
7. 如图，匀速地向此容器内注水，直到把容器注满，在注水过程中，下列图象能大致反映水面高度h随注水时间t变化规律的是（）

A、 B、 C、 D、

查看试题解析
8. 已知 $a_{1} ， a_{2} ， \dots ， a_{2020}$ 都是正数，如果（） $M = (a_{1} + a_{2} + \dots + a_{2019}) (a_{2} + a_{3} + \dots + a_{2020}) ， N = (a_{1} + a_{2} + \dots +$ $a_{2020}) (a_{2} + a_{3} + \dots + a_{2019})$ ，那么 $M 、 N$ 的大小关系是（）

A、 $M > N$ B、 $M = N$ C、 $M < N$ D、不确定

查看试题解析

二、填空题(共5小题,每小题3分,计15分)

9. 用科学记数法表示：-0.00000202=.

查看试题解析
10. 如图所示：已知 $∠ A B D = ∠ A B C$ ，请你补充一个条件：，使得 $△ A B D ≅ △ A B C$ .(只需填写一种情况即可)

查看试题解析
11. 某商店进了一批货，每件进价为4元，售价为每件6元，如果售出 $x$ 件，售出 $x$ 件的总利润为 $y$ 元，则 $y$ 与 $x$ 的函数关系式为.

查看试题解析
12. 如图， $△ A B C$ 中， $D E$ 垂直平分 $B C$ ，若 $△ A B D$ 的周长为 $10 ， A B = 4$ ，则 $A C =$ .

查看试题解析
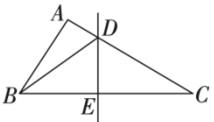13. 如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要cm．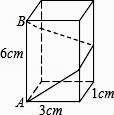

查看试题解析

三、解答题(共11小题,计81分.解答应写出过程)

14. 计算：

(1)、 ${(2 x^{2})}^{3} + x^{4} \cdot x^{2} + {(- 2 x^{2})}^{3}$ ；

(2)、 $| - \frac{1}{2} | + {(π - 3)}^{0} + {(- 1)}^{2016} - {(\frac{1}{3})}^{- 1}$ .

查看试题解析
15. 化简求值： $[(x + y) (x - y) - {(x - y)}^{2}] \div 2 y - y (4 y - 1)$ ，其中 $| x - 3 | + {(y + \frac{1}{2})}^{2} = 0$ .

查看试题解析
16. 如图，用尺规在 $A D$ 的右侧作 $∠ D C P = ∠ D A B$ (不写作法，只需保留作图痕迹).

查看试题解析
17. 如图，直线 $a / / b$ ，点 $B$ 在直线 $b$ 上，且 $A B ⊥ B C ， ∠ 1 = 35^{\circ}$ ，求 $∠ 2$ 的度数.

查看试题解析
18. 某校欲举办文艺汇演活动，小丽和小芳都想当节目主持人，但现在只有一个名额.小丽想出了一个办法，她将一个转盘(质地均匀)平均分成6份.如图所示，游戏规定：随意转动转盘，若指针指到3，则小丽去；若指针指到2，则小芳去；若指针指到其他数字或指在线上，则重转.这个游戏规定对双方公平吗?为什么?若不公平，请修改游戏规定，使这个游戏对双方公平.

查看试题解析
19. 一个零件的形状如图所示，按规定， $∠ A = 90^{\circ} ， ∠ B$ 和 $∠ C$ 分别是 $32^{\circ}$ 和 $21^{\circ}$ 的零件为合格零件.现质检工人量得 $∠ B D C = 149^{\circ}$ ，就断定这个零件不合格，请你运用三角形的有关知识说明零件不合格的理由.

查看试题解析
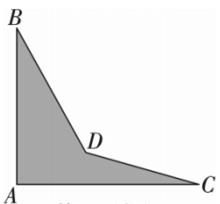20. 完成下面的证明过程.
已知：如图， $A B / / C D ， A E ⊥ B D$ 于 $E ， C F ⊥ B D$ 于 $F ， B F = D E$ .

求证： $△ A B E ≅ △ C D F$ .

证明： $∵ A B / / C D ， ∴ ∠ 1 =$ ▲ (两直线平行，内错角相等).

$∵ A E ⊥ B D ， C F ⊥ B D$ ，

$∴ ∠ A E B =$ ▲ $= 90^{\circ}$

$∵ B F = D E$ ，

$∴ B E =$ ▲

在 $△ A B E$ 和 $△ C D F$ 中， ${\begin{cases} ∠ 1 =_____ \\ B E =_____ \\ ∠ A E B =_____ \end{cases}$

$∴ △ A B E ≅ △ C D F$ （）.

查看试题解析
21. 已知：点 $A 、 E 、 D 、 C$ 在同一条直线上， $A E = C D ， E F / / B D ， E F = B D$ .求证： $A B / / C F$ .

查看试题解析

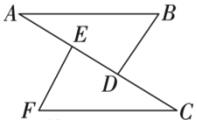22. 受疫情影响，各类学校纷纷延迟开学时间，教育部提倡“停课不停教，停课不停学”的在线教学方式.寒假期间，线上教育的用户使用量猛增，现“钉钉”平台整理出“线上教学项目的投人资金

x

及预计利润

y

之间的一组数据，如下表：

投入资金x/亿元	1	2	3	4	5	6	7
预计利润y/千万元	0.3	0.5	0.7	0.9	1.1	1.3	1.5

(1)、如表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?

(2)、如果预计获得

1.1

千万元的利润，投人资金应为亿元；

(3)、根据表中数据写出两者关系式，如果公司可以拿出10亿元进行“线上教学”项目的投资，预计利润是多少?

查看试题解析

23. 阅读下面材料，然后解答问题：
我们新定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.

(1)、①根据奇异三角形的定义，请你判断：等边三角形一定是奇异三角形吗?▲ ；(填“是”或“不是”)
②若某三角形的三边长分别为 $1 ， \sqrt{7} ， 2$ ，试判断该三角形是否为奇异三角形；

(2)、在Rt $△ A B C$ 中，三边长分别是 $a ， b ， c$ ，且 $a^{2} = 50 ， c^{2} = 100$ ，则这个三角形是否为奇异三角形?请说明理由.

查看试题解析
24. 如图1，点 $A ， B$ 在直线 $l_{1}$ 上，点 $C ， D$ 在直线 $l_{2}$ 上， $A E$ 平分 $∠ B A C ， C E$ 平分 $∠ A C D$ ，且 $∠ E A C + ∠ A C E = 90^{\circ}$ .

(1)、判断直线 $l_{1}$ 与 $l_{2}$ 的位置关系，并说明理由；

(2)、如图2，若 $l_{1} / / l_{2} ， P$ 为直线 $A C$ 上一定点， $Q$ 为直线 $l_{2}$ 上一动点，当点 $Q$ 在直线 $l_{2}$ 上运动时(不与点 $C$ 重合)，猜想 $∠ C P Q ， ∠ C Q P$ 与 $∠ B A C$ 之间的数量关系，并说明理由.

查看试题解析