陕西省渭南市华州区2021_2022学年八年级下学期期末教学质量检测数学试卷

试卷更新日期：2022-08-18 类型：期末考试

进入出卷网下载

一、选择题(共8小题,每小题3分,计24分.的)

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x - 2}{x + 3}$ 的值等于0，则 $x$ 的值是（）

A、2 B、-2 C、3 D、-3

查看试题解析
3. 如图所示，四边形 $A B C D$ 是平行四边形，点 $E$ 在线段 $B C$ 的延长线上，若 $∠ D C E = 132^{\circ}$ ，则 $∠ A =$ （）

A、 $38^{\circ}$ B、 $48^{\circ}$ C、 $58^{\circ}$ D、 $66^{\circ}$

查看试题解析
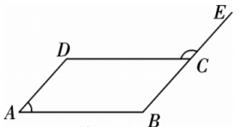4. 在平面直角坐标系中，将点A（−1，2）向右平移3个单位长度得到点B，则点B关于x轴的对称点C的坐标是（）

A、（−4，−2） B、（2，2） C、（−2，2） D、（2，−2）

查看试题解析
5. 如图，在 $▱ A B C D$ 中，对角线 $A C ， B D$ 相交于点 $O$ ，点 $E$ 是边 $A B$ 的中点.已知 $B C = 10 ， A B = 8$ ，则 $O E =$ （）

A、4 B、5 C、6 D、 $2 \sqrt{41}$

查看试题解析
6. 若 $4 x^{2} + (k - 1) x + 9$ 能用完全平方式分解因式，则 $k$ 的值为（）

A、±6 B、±12 C、-13或11 D、13或-11

查看试题解析
7. 如图，在Rt $△ A B C$ 中， $∠ C = 90^{\circ}$ ，以顶点 $A$ 为圆心，适当长度为半径画弧，分别交 $A C 、 A B$ 于点 $M 、 N$ ，再分别以点 $M 、 N$ 为圆心，大于 $\frac{1}{2} M N$ 的长度为半径画弧，两弧交于点 $P$ ，作射线 $A P$ 交 $B C$ 于点 $D$ ，若 $C D = 5 ， A B = 18$ ，则 $△ A B D$ 的面积是（）

A、15 B、30 C、45 D、60

查看试题解析
8. 某运行程序如图所示，规定：从“输人一个值 $x$ ”到“结果是否大于95”为一次程序操作，如果程序操作进行了两次才停止，那么 $x$ 的取值范围是（）

A、 $x > 23$ B、 $23 < x \leq 47$ C、 $11 \leq x < 23$ D、 $x \leq 47$

查看试题解析

二、填空题(共6小题,每小题3分,计18分)

9. 因式分解： $x^{3} y - 4 x y$ = ．

查看试题解析
10. 如图，六边形 $A B C D E F$ 的内角都相等， $A D / / B C$ ，则 $∠ D A B =$ .

查看试题解析
11. 如果 $a - b = 3 ， a b = 7$ ，那么 $a^{2} b - a b^{2}$ 的值是.

查看试题解析
12.
如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到，则点P的坐标为．

查看试题解析
13. 如图，Rt $△ A B C$ 的斜边 $A B$ 的垂直平分线 $M N$ 与 $A C$ 交于点 $M ， ∠ A = 15^{\circ}$ ， $B M = 4$ ，则 $△ A M B$ 的面积为.

查看试题解析
14. 如图，在Rt $△ A B C$ 中， $∠ B = 90^{\circ} ， A B = 4 ， B C > A B$ ，点 $D$ 在 $B C$ 上，以 $A C$ 为对角线的所有平行四边形 $A D C E$ 中， $D E$ 的最小值是.

查看试题解析

三、解答题(共12小题,计78分.)

15. 先化简，再求值： $(\frac{1}{x + 1} - 1) \div \frac{x}{x^{2} - 1}$ ，其中 $x = \sqrt{2} + 1$ .

查看试题解析
16. 已知 $a ， b 、 c$ 是 $△ A B C$ 的三边的长，若满足 $(a - b) b - (b - a) c = 0$ ，试判断此三角形的形状.

查看试题解析
17. 解分式方程： $\frac{x}{x - 2} - 1 = \frac{8}{x^{2} - 4}$ .

查看试题解析
18. 如图，已知线段 $a$ ，求作等腰直角三角形，使其斜边等于线段 $a$ (保留作图痕迹，不必写作法).

查看试题解析
19. 解不等式组： ${\begin{array}{l} \frac{1 + x}{6} > \frac{2 x - 5}{3} + 1 \\ 5 x + 3 \geq 4 x - 1 ， \end{array}$ 并写出其中的正整数解.

查看试题解析
20. 如图， $A D$ 平分 $∠ B A C ， A D ⊥ B D$ ，垂足为点 $D ， D E / / A C$ .求证： $△ B D E$ 是等腰三角形.

查看试题解析
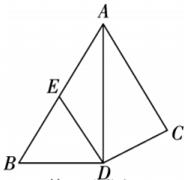21. 如图，已知一次函数 $y = k x + k + 1$ 的图象与一次函数 $y = - x + 4$ 的图象交于点 $A (1 ， a)$ .

(1)、求 $a ， k$ 的值；

(2)、根据图象，写出不等式 $- x + 4 > k x + k + 1$ 的解集；

(3)、结合图象，当 $x > 2$ 时，求一次函数 $y = - x + 4$ 函数值 $y$ 的取值范围.

查看试题解析
22. 如图，在 $▱ A B C D$ 中， $E 、 F$ 是对角线 $A C$ 上的两点，且 $A E = C F$ .

(1)、求证：四边形 $B F D E$ 是平行四边形；

(2)、若 $E F = 2 A E = 2 ， ∠ A C B = 45^{\circ}$ ，且 $B E ⊥ A C$ 于点 $E$ ，求四边形 $A B C D$ 的面积.

查看试题解析
23. 小刚家到学校的距离是1800米．某天早上，小刚到学校后发现作业本忘在家中，此时离上课还有20分钟，于是他立即按原路跑步回家，拿到作业本后骑自行车按原路返回学校．已知小刚骑自行车时间比跑步时间少用了4.5分钟，且骑自行车的平均速度是跑步的平均速度的1.6倍．

(1)、求小刚跑步的平均速度；

(2)、如果小刚在家取作业本和取自行车共用了3分钟，他能否在上课前赶回学校？请说明理由．

查看试题解析
24. 如图，在 $▱ A B C D$ 中， $E$ 是 $A D$ 的中点， $F$ 是 $B C$ 的延长线上一点，且 $C F = \frac{1}{2} B C$ ，连接 $C E ， D F$ .

(1)、求证：四边形 $C E D F$ 是平行四边形；

(2)、若 $A B = 4 ， A D = 6 ， ∠ B = 60^{\circ}$ ，求 $D F$ 的长.

查看试题解析
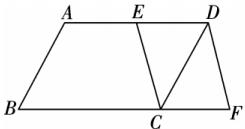25. 某苹果基地销售优质苹果，该基地对需要送货且购买量在 $2000 kg \sim 5000 kg$ (含 $2000 kg$ 和 $5000 kg$ )的客户有两种销售方案(客户只能选择其中一种方案)：
方案 $A$ ：每千克5.8元，由基地免费送货；

方案 $B ：$ 每千克5元，客户需支付运费2000元.

(1)、请分别写出按方案 $A$ 、方案 $B$ 购买这种苹果的应付款 $y$ (元)与购买量 $x (kg)$ 之间的函数表达式；

(2)、求购买量 $x$ 在什么范围时，选用方案 $A$ 比方案 $B$ 付款少；

(3)、某水果批发商计划用20000元选用这两种方案中的一种购买尽可能多的这种苹果，请写出他应选择哪种方案.

查看试题解析
26. 如图，在平面直角坐标系中， $A B / / O C ， A (0 ， 12) ， B (a ， c) ， C (b ， 0)$ ，且 $a ， b$ 满足 $| a - 21 | + {(b - 16)}^{2} = 0$ ，一动点 $P$ 从点 $A$ 出发，在线段 $A B$ 上以每秒2个单位长度的速度向点 $B$ 运动；动点 $Q$ 从点 $O$ 出发，在线段 $O C$ 上以每秒1个单位长度的速度向点 $C$ 运动，点 $P ， Q$ 分别从点 $A$ ， $O$ 同时出发，当点 $P$ 运动到点 $B$ 时停止运动，点 $Q$ 随之停止运动.设运动时间为 $t$ 秒.

(1)、求 $B ， C$ 两点的坐标；

(2)、当 $t$ 为何值时，四边形 $P Q C B$ 是平行四边形?请求出此时 $P$ ， $Q$ 两点的坐标；

(3)、当 $t$ 为何值时， $△ P Q C$ 是以 $P Q$ 为腰的等腰三角形?请求出此时 $P ， Q$ 两点的坐标.

查看试题解析