陕西省榆林市子洲县2021-2022学年七年级下学期期末数学试卷
试卷更新日期：2022-08-18 类型：期末考试
一、选择题（共8小题，每小题3分，满分24分）
-
1. 如图“表情图”中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 华为作为世界顶级科技公司，设计的麒麟90005GSoc芯片，拥有领先的5nm制程和架构设计，5nm＝0.000000005m，将0.000000005用科学记数法表示为（ ）A、5×10﹣7 B、5×10﹣8 C、5×10﹣9 D、5×10﹣103. 计算：（﹣a2b）2•a2＝（ ）A、a4b2 B、a6b2 C、a5b2 D、a8b24. 已知等腰△ABC中，∠A＝50°，则∠B的度数为（ ）A、50° B、65° C、50°或65° D、50°或65°或80°5. 如图，直线AB，CD相交于点O，∠AOC＝75°，OE把∠BOD分成两部分，且∠BOE：∠EOD＝1：2，则∠AOE的度数为（ ）
A、165° B、155° C、150° D、130°6. 如图，点E是△ABC的边AC的中点，过点C作CF∥AB，连接FE并延长，交AB于点D，若AB＝9，CF＝6，则BD的长为（ ）
A、2 B、2.5 C、3 D、4.57. 一个小球在如图所示的方格地砖上任意滚动，并随机停留在某块地砖上，每块地砖的大小、质地完全相同，那么该小球停留在阴影区域的概率是（ ）
A、 B、 C、 D、8. 如表反映的是某地区电的使用量x（千瓦•时）与应交电费y（元）之间的关系，根据表格判断，下列说法不正确的是（ ）用电量x（千瓦•时）
1
2
3
4
…
应交电费y（元）
0.55
1.1
1.65
2.2
…
A、x与y都是变量，且x是自变量，y是因变量 B、用电量每增加1千瓦•时，电费增加0.55元 C、若用电量为8千瓦•时，则应交电费4.4元 D、若所交电费为2.75元，则用电量为6千瓦•时二、填空题（共5小题，每小题3分，共15分）
-
9. 已知∠A＝38°，则∠A的余角为 °．10. 已知某三角形的两条边长分别为4和9，则其第3三边的长可能是 ． （写出一个即可）11. 已知一个三角形的面积等于8x3y2﹣4x2y3 ， 一条边长等于8x2y2 ， 则这条边上的高等于 ．12. 按照如图所示的计算程序，y与x之间的关系式为 ．
13. 如图，在△ABC中，AB＝AC，AD是BC边上的中线，在AD上取一点E，连接CE，使得AE＝CE，若∠ECD＝20°，则∠B＝°．
三、解答题（共13小题，满分81分）
-
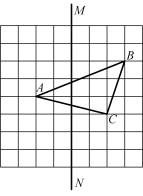
14. 计算：（）﹣2+（﹣1）2022+（）0 ．15. 运用乘法公式计算：397×403+9．16. 如图，在正方形网格中，点A、B、C都在格点上，作 关于直线MN对称的图形 ．
17. 如图，已知△ABC，利用尺规在BC上找一点D，使得∠BAD＝∠CAD．（保留作图痕迹，不写作法）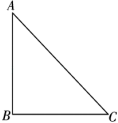
18. 某班在爱心义卖活动中设立了一个可以自由转动的转盘，如图所示，同时规定：顾客购物满50元就能获得一次转动转盘的机会，如表是活动中的统计数据：转动转盘的次数n
100
200
300
400
500
落在“谢谢参与”区域的次数m
29
60
93
122
b
落在“谢谢参与”区域的频率
0.29
0.3
0.31
a
0.296
(1)、填空：a＝ ， b＝ ．(2)、若继续转动转盘，当n很大时，落在“谢谢参与！”区域的频率将会接近多少？若晓慧去转动该转盘一次，则她转到“谢谢参与！”的概率约是多少？（结果保留一位小数）19. 小明家距离公园8千米，一天早晨，小明骑车去公园途中自行车出现故障，他于原地修车，车修好后，立即在确保安全的前提下以更快的速度匀速骑行到达公园．如图反映的是小明去公园过程中骑行的路程（千米）与他所用的时间（分钟）之间的关系，请根据图象，解答下列问题：
(1)、小明骑行了 千米时，自行车出现故障；(2)、小明修车用了 分钟；(3)、求自行车出现故障前小明骑行的平均速度．20. 如图，在△ABC中，∠BAC＝105°，MP垂直平分AB，分别交AB、BC于点M、P，NQ垂直平分AC，分别交AC．BC于点N、Q，连接AP、AQ，求∠PAQ的度数．
21. 如图，在四边形ABCD中，E是对角线AC上一点，连接DE，AD∥BC，AC＝AD，∠CED+∠B＝180°．△ADE与△CAB全等吗？为什么？
22. 先化简，再求值：x（x+4）﹣（x﹣6）（x+2）+（3x2﹣x）+x，其中x＝﹣1．23. 如图是一个工业开发区局部的设计图，河的同一侧有两个工厂A和B，AD、BC的长表示两个工厂到河岸的距离，其中E是进水口，D、C为两个排污口．已知AE＝BE，∠AEB＝90°，AD⊥DC，BC⊥DC，点D、E、C在同一直线上，AD＝150米，BC＝350米，求两个排污口之间的水平距离DC．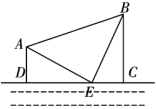
24. 如图，AB∥CD，AH与BC交于点F，点D在AH上，∠1＝∠2．
(1)、判断BC与DE平行吗？为什么？(2)、若∠1＝110°，∠A＝50°，求∠C的度数．25. 在一个不透明的袋子中装了4个红球和6个白球，这些球除颜色外都相同．(1)、下列事件中：不可能事件是 ， 必然事件是 ， 随机事件是 ；（填序号）①从袋子中同时摸出2个球都是红球；
②从袋子中摸出1个球是黑球；
③从袋子中同时摸出5个球至少有一个是白球．
(2)、求从袋子中随机摸出1个球是红球的概率；(3)、小宇从袋子中取出m个白球，同时又放入相同数目的红球，发现随机摸出一个球是红球的概率为 ， 求m的值．26. 如图，在Rt△ABC和Rt△EFD中，∠ABC＝∠EFD＝90°，AC＝ED，AC⊥ED，垂足为M，连接AE、CE．
(1)、△ABC与△EFD全等吗？为什么？(2)、若∠AEF＝∠DEF，判断∠AEC与∠ACE的数量关系，并说明理由．