陕西省咸阳市泾阳县2021-2022学年七年级下学期期末数学试卷
试卷更新日期：2022-08-18 类型：期末考试
一、选择题（共8小题，每小题3分，计24分。）
-
1. 计算：（﹣20）0＝（ ）A、0 B、20 C、1 D、﹣202. 下列“表情图”中，属于轴对称图形的是A、
B、
C、
D、
3. 如图，AB∥CD，直角三角尺的直角顶点在CD上，如果∠1＝28°，那么∠2的度数为（ ）
A、28° B、62° C、56° D、72°4. 变量x与y之间的关系式是y＝35x+20，当自变量x＝2时，因变量y的值是（ ）A、90 B、65 C、70 D、755. 计算：（﹣a2b）2•a2＝（ ）A、a4b2 B、a6b2 C、a5b2 D、a8b26. 下列说法正确的是（ ）A、长度为2cm、3cm和5cm的三条线段首尾相接可以组成三角形 B、面积相等的两个三角形全等 C、两直线被第三条直线所截，同位角相等 D、等角的补角相等7. 如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于D．如果AC＝10cm，那么AE+DE等于（ ）
A、6cm B、8cm C、10cm D、12cm8. 某施工队修一段长度为360米的公路，施工队每天的效率相同，如表根据每天工程进度制作而成的．施工时间/天
1
2
3
4
5
6
7
……
累计完成施工量/米
30
60
90
120
150
180
210
……
下列说法错误的是（ ）
A、随着施工时间的逐渐增大，累计完成施工量也逐渐增大 B、施工时间每增加1天，累计完成施工量就增加30米 C、当施工时间为9天时，累计完成施工量为270米 D、若累计完成施工量为330米，则施工时间为10天二、填空题（共5小题，每小题3分，计15分）
-
9. 医用口罩可以过滤小至0.000004米颗粒，用科学记数法表示0.000004是 ．10. 多项式A与2x的积为2x2+14x，则A＝ ．11. 如图，直线AB、CD、EF相交于点O，若∠1+∠2＝150°，则∠3＝°．
12. 有7张纸签，分别标有数字1，1，2，2，3，4，5，从中随机地抽出一张．抽出标有数字1的纸签的概率是 ．13. 如图，D是AB延长线上一点，DF交AC于点E，AE＝CE，FC∥AB，若AB＝3，CF＝5，则BD的长是 ．
三、解答题（共13小题，计81分.）
-
14. 计算：2﹣2+42022 ．15. 某班在爱心义卖活动中设立了一个可以自由转动的转盘，如图所示，同时规定：顾客购物满50元就能获得一次转动转盘的机会，如表是活动中的统计数据：
转动转盘的次数n
100
200
300
400
500
落在“谢谢参与！”区域的次数m
29
60
93
122
b
落在“谢谢参与！”区域的频率
0.29
0.3
0.31
a
0.29
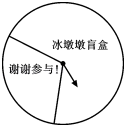(1)、填空：a＝ ， b＝；(2)、若继续转动转盘，当n很大时，落在“谢谢参与！”区域的频率将会接近多少？若晓慧去转动该转盘一次，则她转到“谢谢参与！”的概率约是多少？（结果保留一位小数）16. 先化简，再求值：（2x﹣1）2+（x+6）（x﹣2），其中x＝2．17. 如图，已知△ABC，请利用尺规作图法在AC上求作一点P，使得BP平分∠ABC．（保留作图痕迹，不写作法）
18. 如图，圆柱的底面半径是1cm，圆柱的高由小到大变化，圆柱的侧面积随高的变化而变化．（结果保留π）
(1)、在这个变化过程中，自变量和因变量各是什么？求圆柱的侧面积S（ ）与圆柱的高h（cm）之间的关系式；(2)、当圆柱的高为2cm时，圆柱的侧面积是多少？19. 如图，△ABC的顶点均在网格的格点上，△A1B1C1与△ABC关于直线m对称，点A、B、C的对应点分别是A1、B1、C1 ．
⑴在图中画出△A1B1C1；
⑵点B1与点B2关于直线n对称，请画出直线n．
20. 如图，在△ABC中，AF平分∠BAC交BC于点F，AC的垂直平分线交BC于点E，交AC于点D，∠B＝60°，∠C＝26°，求∠FAE的度数．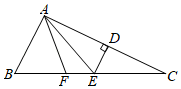
21. 在学习完“探索三角形全等的条件”一节后，小丽总结出很多全等三角形的模型，她设计了以下问题给同桌解决：如图，做一个“U”字形框架PABQ，AP，BQ足够长，PA⊥AB于点A，QB⊥AB于点B，她在框架里放了两根长度相等的木条CM、NM，且CM⊥MN，点C、M、N分别在PA、AB、BQ上，若AM＝4cm，求BN的长．
22. 如图，有一块长方形板材ABCD，长AD为2acm（a＞2），宽AB比长AD少4cm，若扩大板材，将其长和宽都增加2cm．
(1)、板材原来的面积（即长方形ABCD的面积）是多少平方厘米？(2)、板材面积增加后比原来多多少平方厘米？23. 某中学七年级开展了“双减”下劳动实践活动，组织学生到实践基地割麦．张敏与同学从学校出发到实践基地，割完麦后，按原路返回．途中到小卖部买水，然后返回学校，张敏与同学离学校的距离y（米）与所用时间x（分钟）之间的关系如图所示．学校、小卖部、实践基地在同一直线上．
(1)、学校到实践基地的距离为 m，小卖部到实践基地的距离为 m；(2)、张敏与同学在实践基地停留了多长时间？他们在小卖部买水用了多长时间？(3)、若他们上午8：00从学校出发，那么他们几点回到学校？24. 如图，直线EF分别交直线AB、CD于点E、F，EP平分∠AEF交CD于点P，点N是射线PC上一点，延长EP到点M，使得PM＝PN，连接MN．
(1)、若AB∥CD，∠EFD＝80°，求∠AEP的度数；(2)、若∠PMN＝72.5°，∠AEF＝70°，判断直线AB与CD是否平行？并说明理由．25. 在一个不透明的袋子中装了4个红球和6个白球，这些球除颜色外都相同．(1)、下列事件中：不可能事件是 ， 必然事件是 ， 随机事件是 ；（填序号）①从袋子中同时摸出2个球都是红球；
②从袋子中摸出1个球是黑球；
③从袋子中同时摸出5个球至少有一个是白球．
(2)、求从袋子中随机摸出1个球是红球的概率；(3)、小宇从袋子中取出m个白球，同时又放入相同数目的红球，发现随机摸出一个球是红球的概率为 ， 求m的值．26. 如图，已知△ABC是等腰三角形，CA＝CB，∠ACB是锐角，∠ACB＝α．点M在边AC上，点N在边BC上（点M、点N不与所在线段端点重合），BN＝AM，连接AN，BM，射线AG∥BC，延长BM交射线AG于点D，点E在NA的延长线上，且AE＝DE．
(1)、△BCM与△ACN全等吗？请说明理由；(2)、请求出∠BDE的度数．（用含α的代数式表示）