浙江省绍兴市上虞区2021-2022学年七年级下学期期末数学适应性试卷
试卷更新日期:2022-08-18 类型:期末考试
一、选择题(本大题共10小题,共30分。)
-
1. 要使分式有意义,则的取值应满足( )A、 B、 C、 D、2. 下列因式分解结果正确的是( )A、 B、 C、 D、3. 下列各组数中,是二元一次方程的解的是( )A、 B、 C、 D、4. 如图,将△ABC沿BC方向平移1cm 得到对应的△A'B'C'.若B'C=2cm,则BC'的长是( )
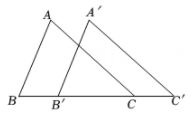 A、2cm B、3cm C、4cm D、5cm5. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线 , , 贝贝、晶晶、欢欢三位同学的做法如图所示:
A、2cm B、3cm C、4cm D、5cm5. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线 , , 贝贝、晶晶、欢欢三位同学的做法如图所示:
上述三位同学的做法中,依据“内错角相等,两直线平行”的是( )A、仅贝贝同学 B、贝贝和晶晶 C、晶晶和欢欢 D、贝贝和欢欢6. 下列运算正确的是( )A、 B、 C、 D、7. 如图是某种学生快餐(共400g)营养成分扇形统计图,已知其中表示脂肪的扇形的圆心角为 , 维生素和矿物质含量占脂肪的一半,蛋白质含量比碳水化合物多40g有关这份快餐,下列说法正确的是( ) A、表示维生素和矿物质的扇形的圆心角为 B、脂肪有44g,含量超过10% C、表示碳水化合物的扇形的圆心角为 D、蛋白质的含量为维生素和矿物质的9倍8. 如图, , 平分 , 且 , 垂足为 , 则与的数量关系是( )
A、表示维生素和矿物质的扇形的圆心角为 B、脂肪有44g,含量超过10% C、表示碳水化合物的扇形的圆心角为 D、蛋白质的含量为维生素和矿物质的9倍8. 如图, , 平分 , 且 , 垂足为 , 则与的数量关系是( ) A、 B、 C、 D、9. 某工程队承接了60万平方米的绿化工程,由于情况有变,设原计划每天绿化的面积为万平方米,列方程为 , 根据方程可知省略的部分是( )A、实际工作时每天的工作效率比原计划提高了20%,结果提前30天完成了这一任务 B、实际工作时每天的工作效率比原计划提高了20%,结果延误30天完成了这一任务 C、实际工作时每天的工作效率比原计划降低了20%,结果延误30天完成了这一任务 D、实际工作时每天的工作效率比原计划降低了20%,结果提前30天完成了这一任务10. 如图(1)是一段长方形纸带, , 将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数为( )
A、 B、 C、 D、9. 某工程队承接了60万平方米的绿化工程,由于情况有变,设原计划每天绿化的面积为万平方米,列方程为 , 根据方程可知省略的部分是( )A、实际工作时每天的工作效率比原计划提高了20%,结果提前30天完成了这一任务 B、实际工作时每天的工作效率比原计划提高了20%,结果延误30天完成了这一任务 C、实际工作时每天的工作效率比原计划降低了20%,结果延误30天完成了这一任务 D、实际工作时每天的工作效率比原计划降低了20%,结果提前30天完成了这一任务10. 如图(1)是一段长方形纸带, , 将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数为( )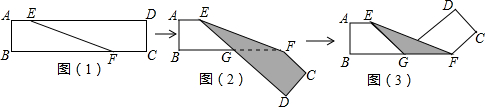 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24分)
-
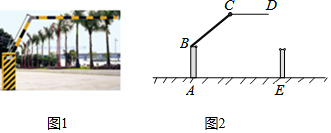
11. 想要了解本周天气的变化情况,最适合采用统计图(填“扇形”、“折线”或“条形”).12. 已知方程组 , 则的值为 .13. 已知是一个完全平方式,那么 .14. 《九章草术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有辆车,人数为 , 根据题意可列方程组为 .15. 生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,垂直于地面于 , 平行于地面 , 则
 16. 某感冒药用来计算儿童服药量的公式为 , 其中为成人服药量,为儿童的年龄 , 如果一个儿童的服药量恰好是成人服药量的 , 那么他的年龄是 岁17. 小明在拼图时,发现8个一样大小的长方形如图1那样,恰好可以拼成一个大的长方形.小红看见了,说:“我来试一试.”结果小红七拼八凑,拼成如图2那样的正方形.“咳,怎么中间还留了一个洞,恰好是边长为的小正方形”请你写出这些长方形的长和宽 .
16. 某感冒药用来计算儿童服药量的公式为 , 其中为成人服药量,为儿童的年龄 , 如果一个儿童的服药量恰好是成人服药量的 , 那么他的年龄是 岁17. 小明在拼图时,发现8个一样大小的长方形如图1那样,恰好可以拼成一个大的长方形.小红看见了,说:“我来试一试.”结果小红七拼八凑,拼成如图2那样的正方形.“咳,怎么中间还留了一个洞,恰好是边长为的小正方形”请你写出这些长方形的长和宽 . 18. 如图,已知 , 于点 , 点在直线上,且位于直线的右侧.
18. 如图,已知 , 于点 , 点在直线上,且位于直线的右侧. (1)、若 , 则的度数是;(2)、若 , , 则的度数是 .
(1)、若 , 则的度数是;(2)、若 , , 则的度数是 .三、解答题(本大题共6小题,共46分。)
-
19. 分解因式(1)、;(2)、 .20.(1)、计算:;(2)、先化简,再求值: , 其中 , .21. 解方程:(1)、;(2)、 .22. 小聪、小明参加了100米跑的5期集训,每期集训结束时进行测试.根据他们集训时间、测试成绩绘制成如下两个统计图.
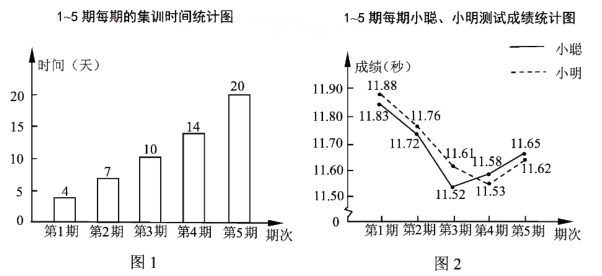
根据图中信息,解答下列问题:
(1)、这5期的集训共有多少天?(2)、哪一期小聪的成绩比他上一期的成绩进步最多?进步了多少秒?(3)、根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,简要说说你的想法.23. 为创建省文明卫生城市,某街道将一公园进行绿化改造.计划种植甲、乙两种花木,甲种花木每棵进价800元,乙种花木每棵进价3000元,共需107万元;每种植一棵甲种花木需人工费30元,每种植一棵乙种花木需人工费80元,共需人工费32000元。(1)、求计划种植甲、乙两种花木各多少棵?(2)、如果承包植树的老板安排28人同时种植这两种花木,每人每天能种植甲种花木20棵或乙种花木5棵,应分别安排多少人种植甲种花木和乙种花木,才能确保同时完成各自的任务?24. 已知 , (1)、如图1,若 , , 求的度数;(2)、如图2,若平分 , 平分 , 则与有怎样的数量关系,并说明理由;(3)、如图3,若平分 , 平分 , 则与有怎样的数量关系,并说明理由.
(1)、如图1,若 , , 求的度数;(2)、如图2,若平分 , 平分 , 则与有怎样的数量关系,并说明理由;(3)、如图3,若平分 , 平分 , 则与有怎样的数量关系,并说明理由.