浙江省金华市婺城区2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-18 类型：期末考试

进入出卷网下载

一、选择题（共10小题，共30分.）

1. 使 $\sqrt{x - 2}$ 有意义的 $x$ 的取值范围为（）

A、 $x \geq 2$ B、 $x > 2$ C、 $x \leq 2$ D、 $x < 2$

查看试题解析
2. 下列计算正确的是（）

A、 $3 + \sqrt{3} = 3 \sqrt{3}$ B、 $2 \sqrt{3} + \sqrt{3} = 3 \sqrt{3}$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$

查看试题解析
3. 如图是厨余垃圾、可回收物、有害垃圾和其他垃圾的标识，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在▱ $A B C D$ 中，若 $∠ A + ∠ C = 110 °$ ，则 $∠ B$ 的度数是（）

A、 $70 °$ B、 $105 °$ C、 $125 °$ D、 $135 °$

查看试题解析
5. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(2 ， 1)$ ，则下列各点中，不在该函数图象上的是（）

A、 $(1 ， 2)$ B、 $(- 1 ， - 2)$ C、 $(- 2 ， - 1)$ D、 $(- 2 ， 1)$

查看试题解析
6. 测试五位学生的“一分钟仰卧起坐”成绩，得到五个各不相同的数据. 在统计时，出现了一处错误：将最高成绩50个写成了55个.则下列统计量不受影响的是（）

A、方差 B、标准差 C、中位数 D、平均数

查看试题解析
7. 用反证法证明命题“若在 $△ A B C$ 中， $A B \neq A C$ ，则 $∠ B \neq ∠ C$ ”时，首先应假设（）

A、 $∠ A = ∠ B$ B、 $A B = A C$ C、 $∠ A = ∠ C$ D、 $∠ B = ∠ C$

查看试题解析
8. 下列关于 $x$ 的一元二次方程中，有两个不相等实数根的方程是（）

A、 $x^{2} + 1 = 0$ B、 $x^{2} - x + 2 = 0$ C、 $x^{2} - 2 x + 1 = 0$ D、 $x^{2} - 2 x - 2 = 0$

查看试题解析
9. “方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为 $2 c m$ 的正方形 $A B C D$ 沿对角线 $B D$ 方向平移 $1 c m$ 得到正方形 $A' B' C' D'$ ，形成一个“方胜”图案，则点 $D$ ， $B'$ 之间的距离为（）

A、 $1 c m$ B、 $2 c m$ C、 $(\sqrt{2} - 1) c m$ D、 $(2 \sqrt{2} - 1) c m$

查看试题解析
10. 如图1，点 $P$ 为矩形 $A B C D$ 边上的一个动点，点 $P$ 从 $A$ 出发沿着矩形的四条边运动，最后回到 $A .$ 设点 $P$ 运动的路程长为 $x$ ， $△ A B P$ 的面积为 $y$ ，图2是 $y$ 随 $x$ 变化的函数图象，则矩形 $A B C D$ 的对角线 $B D$ 的长是（）

A、 $\sqrt{34}$ B、 $\sqrt{41}$ C、8 D、10

查看试题解析

二、填空题（共6小题，共24分）

11. 当 $x = 1$ 时，二次根式 $\sqrt{x + 3}$ 的值为．

查看试题解析
12. 某天的最低气温是 $- 2 ℃$ ，最高气温是 $10 ℃$ ，则这天气温的极差为 $℃ .$

查看试题解析
13. 如图，为估计池塘岸边 $A$ ， $B$ 两点间的距离，在池塘的一侧选取点 $O$ ，分别取 $O A$ ， $O B$ 的中点 $M$ ， $N$ ，测得 $M N = 16 m$ ，则 $A$ ， $B$ 两点间的距离是 $m .$

查看试题解析
14. 如图，▱ $O A B C$ 的边 $O A$ 在 $x$ 轴上，顶点 $C$ 在反比例函数 $y = - \frac{4}{x} (x < 0)$ 的图象上， $B C$ 与 $y$ 轴相交于点 $D$ ，且 $D$ 为 $B C$ 的中点，则▱ $O A B C$ 的面积为．

查看试题解析
15. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $B E / / A C$ ， $A E / / B D$ ， $O E$ 与 $A B$ 交于点 $F .$ 若 $O E = 5$ ， $A C = 8$ ，则菱形 $A B C D$ 的高为．

查看试题解析
16. 三折伞是我们生活中常用的一种伞，它的骨架是一个“移动副”和多个“转动副”组成的连杆机构，如图1是三折伞一条骨架的结构图，当“移动副”（标号1)沿着伞柄移动时，折伞的每条骨架都可以绕“转动副”（标号2-9）转动；图2是三折伞一条骨架的示意图，其中四边形 $C D E F$ 和四边形 $D G M N$ 都是平行四边形， $A C = B C = 14 c m$ ， $D E = 2 c m$ ， $D N = 1 c m .$ 已知关闭折伞后，点 $A$ 、 $E$ 、 $H$ 三点重合，点 $B$ 与点 $M$ 重合．

(1)、BN= $c m$ ；

(2)、当 $∠ B A C = 60 °$ 时，点 $H$ 到伞柄 $A B$ 距离为 $c m$ ．

查看试题解析

三、解答题（共8小题，共66分。）

17. 计算： ${(- \sqrt{3})}^{2} - \sqrt{16} - \sqrt{{(- 5)}^{2}} + \sqrt{2} \times 3 \sqrt{2}$ ．

查看试题解析
18. 解方程：

(1)、 $x^{2} + 2 x = 0$ ；

(2)、 $x^{2} - 6 x + 2 = 0$ ．

查看试题解析
19. 如图，在▱ $A B C D$ 中，对角线 $A C$ ， $B D$ 交于点 $E$ ， $A C ⊥ B C .$ 若 $A C = 4$ ， $A B = 5.$ 求 $B C$ 与 $B D$ 的长．

查看试题解析
20. 图①、图②、图③均是5×5的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A、B均在格点上．只用无刻度的直尺，在给定的网格中按下列要求画图，所画图形的顶点均在格点上且不全等，不要求写画法．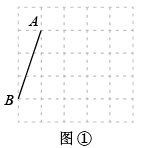

(1)、在图①中以线段AB为边画一个平行四边形．

(2)、在图②中以线段AB为边画一个正方形．

(3)、在图③中以线段AB为边画一个菱形，所画菱形的面积为．

查看试题解析

21. 学校准备从甲乙两位选手中选择一位，代表学校参加所在地区的汉字听写大赛，总评成绩由“表达能力、阅读理解、综合素质和汉字听写”四部分组成．甲，乙两位选手的成绩如下表，请解答下列问题：

选手	表达能力	阅读理解	综合素质	汉字听写
甲	85	78	85	73
乙	73	80	82	83

(1)、由表中成绩已算得甲的平均成绩为80.25，请计算乙的平均成绩．

(2)、已知四部分占总评成绩的比例如图所示．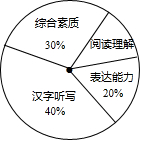

①求图中表示“阅读理解”的扇形的圆心角度数；

②通过计算甲，乙两名选手的总评成绩，你认为学校派谁参加比赛合适？

查看试题解析

22. 金华市区某超市以原价为40元 $/$ 瓶的价格对外销售某种洗手液，为了减少库存，决定降价销售，经过两次降价后，售价为32.4元 $/$ 瓶．

(1)、求平均每次降价的百分率．

(2)、金华市区某学校为确保疫情复学后工作安全、卫生、健康、有序，学校决定购买一批洗手液(超过200瓶）.该超市对购买量大的客户有优惠措施，在32.4元 $/$ 瓶的基础上推出方案一：每瓶打九折；方案二：不超过200瓶的部分不打折，超过200瓶的部分打八折．学校应该选择哪一种方案更省钱？请说明理由．

查看试题解析
23. 已知一块矩形草坪的两边长分别是2米与3米，现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍，设原矩形的一边加长 $a$ 米，另一边长加长 $b$ 米，可得 $a$ 与 $b$ 之间的函数关系式 $b = \frac{12}{a + 3} - 2.$ 某班“数学兴趣小组”对此函数进一步推广，得到更一般的函数 $y = \frac{12}{x + 3} - 2$ ，现对这个函数的图象和性质进行了探究，研究过程如下，请补充完整：

(1)、类比反比例函数可知，函数 $y = \frac{12}{x + 3} - 2$ 的自变量 $x$ 的取值范围是，这个函数值 $y$ 的取值范围是．

(2)、“数学兴趣小组”进一步思考函数 $y = | \frac{12}{x + 3} - 2 |$ 的图象和性质，请根据函数 $y = \frac{12}{x + 3} - 2$ 的图象，画出函数 $y = | \frac{12}{x + 3} - 2 |$ 的图象；

(3)、结合函数 $y = | \frac{12}{x + 3} - 2 |$ 的图象解答下列问题：
①求出方程 $| \frac{12}{x + 3} - 2 | = 0$ 的根；

②如果方程 $| \frac{12}{x + 3} - 2 | = a$ 有2个实数根，请直接写出 $a$ 的取值范围．

查看试题解析
24. 如图，在平面直角坐标系中，矩形 $O A B C$ 的顶点 $A$ ， $B$ 的坐标分别为 $A (0 ， 2)$ ， $B (4 ， 2)$ ，点 $D$ 为对角线 $O B$ 中点，点 $E$ 在 $x$ 轴上运动，连结 $D E$ ，把 $△ O D E$ 沿 $D E$ 翻折，点 $O$ 的对应点为点 $F$ ，连结 $B F$ ．

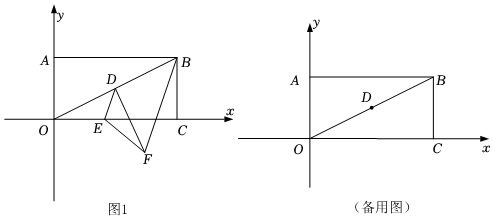(1)、当点 $F$ 在第四象限时（如图1），求证： $D E / / B F$ ．

(2)、当点 $F$ 落在矩形的某条边上时，求 $E F$ 的长．

(3)、是否存在点 $E$ ，使得以 $D$ ， $E$ ， $F$ ， $B$ 为顶点的四边形是平行四边形？若存在，求点 $E$ 的坐标；若不存在，请说明理由．

查看试题解析