四川省广元市剑阁县2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-08-18 类型:期末考试
一、选择题(本题共10小题,共30分)
-
1. 近段时间,以熊猫为原型的2022北京冬奥会吉祥物“冰墩墩”成了全网“顶流” 如图,通过平移如图吉祥物“冰墩墩”可以得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在实数2022、、、3.1415926、、0.3030030003…(相邻两个3之间依次增加1个0)中,无理数有个.( )A、1 B、2 C、3 D、43. 点在第四象限,它到轴、轴的距离分别是3、4,则点的坐标是( )A、 B、 C、 D、4. 如图,将三角尺的直角顶点放在直尺的一边上, , , 则的度数等于( )
2. 在实数2022、、、3.1415926、、0.3030030003…(相邻两个3之间依次增加1个0)中,无理数有个.( )A、1 B、2 C、3 D、43. 点在第四象限,它到轴、轴的距离分别是3、4,则点的坐标是( )A、 B、 C、 D、4. 如图,将三角尺的直角顶点放在直尺的一边上, , , 则的度数等于( ) A、 B、 C、 D、5. 下列调查中,适合抽样调查的是( )A、了解本班同学的某次体质测试成绩情况 B、在“新冠状肺炎”疫情期间,调查某次航班乘客健康码行程码及核酸检测报告 C、了解某批次灯泡的使用寿命情况 D、企业招聘,对应聘人员进行面试6. 将不等式的解集表示在数轴上,正确的是( )A、
A、 B、 C、 D、5. 下列调查中,适合抽样调查的是( )A、了解本班同学的某次体质测试成绩情况 B、在“新冠状肺炎”疫情期间,调查某次航班乘客健康码行程码及核酸检测报告 C、了解某批次灯泡的使用寿命情况 D、企业招聘,对应聘人员进行面试6. 将不等式的解集表示在数轴上,正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 若是关于、的二元一次方程,则的值为( )A、0 B、2 C、0或2 D、1或28. 已知、为常数,若的解集为 , 则的解集是( )A、 B、 C、 D、9. 下列说法中,正确的有个.( )
7. 若是关于、的二元一次方程,则的值为( )A、0 B、2 C、0或2 D、1或28. 已知、为常数,若的解集为 , 则的解集是( )A、 B、 C、 D、9. 下列说法中,正确的有个.( )带根号的数是无理数;是的一个平方根;“垂直于同一条直线的两条直线平行”是假命题;如果 , , 且 , 那么轴.直线外一点、与直线上各点连接的线段中,垂线最短.
A、1 B、2 C、3 D、410. 如图,已知 , 平分 , 且 , 则与的关系是( )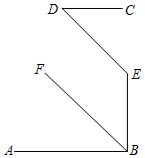 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共6小题,共24分)
-
11. 的平方根为 .12. 为了解“双减”后某地区七年级学生每天做家庭作业所用的时间,从该地区七年级学生中抽取1000名学生进行调查.在这个抽样调查中,样本的容量是 .13. 若将点向下平移4个单位,再向右平移3个单位后得到点 , 那么点的坐标为 .14. 如图 , , 为直线 , 上的两点,且 , , 则与的度数之和为 .
 15. 已知不等式的正整数解恰好是1、2、3,则的取值范围是 .16. 已知某铁路桥长1600米.现有一列火车从桥上通过,测得火车从开始上桥到完全过桥共用90秒,整列火车完全在桥上的时间是70秒,则这列火车长米.
15. 已知不等式的正整数解恰好是1、2、3,则的取值范围是 .16. 已知某铁路桥长1600米.现有一列火车从桥上通过,测得火车从开始上桥到完全过桥共用90秒,整列火车完全在桥上的时间是70秒,则这列火车长米.三、解答题(本题共10小题,共96分)
-
17. 计算: .18. 解下面二元一次方程组 .19. 完成下面的证明过程:
已知:如图, , , 求证: .

证明:已知 ,
,
,
已知 ,
等量代换 ,
,
20. 解不等式组: , 并把解集在数轴上表示出来.21. 联合国规定每年的6月5日是“世界环境日”某校课外活动小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将调查结果分析整理后,制成了下面的两个统计图.
其中:
:能将垃圾放到规定的地方,而且还会考虑垃圾的分类.
:能将垃圾放到规定的地方,但不会考虑垃圾的分类.
:偶尔会将垃圾放到规定的地方.
:随手乱扔垃圾.
根据以上信息回答下列问题:
(1)、该校课外活动小组共调查了多少人?并补全下面的条形统计图;(2)、如果该校共有师生4000人,那么随手乱扔垃圾的约有多少人?22.(1)、平面直角坐标系中,有一点 , 当点到轴距离是1时,求的值.(2)、已知 , .已知的算术平方根为3,求的值;
如果一个正数的平方根分别为、 , 求这个正数.
23. 已知在平面直角坐标系中有三点 , , 请回答如下问题: (1)、在坐标系内描出的位置;(2)、求出的面积;(3)、在轴上是否存在点 , 使以、、三点为顶点的三角形的面积为10,若存在,请直接写出点的坐标;若不存在,请说明理由.24. 如图点、在线段上,点、分别在线段和上, , .
(1)、在坐标系内描出的位置;(2)、求出的面积;(3)、在轴上是否存在点 , 使以、、三点为顶点的三角形的面积为10,若存在,请直接写出点的坐标;若不存在,请说明理由.24. 如图点、在线段上,点、分别在线段和上, , . (1)、判断与的位置关系,并说明理由;(2)、若是的平分线, , 且::10,试说明与有怎样的位置关系?25. 某电器超市销售每台进价分别为200元、170元的、两种型号的电风扇,下表是近两周的销售情况:
(1)、判断与的位置关系,并说明理由;(2)、若是的平分线, , 且::10,试说明与有怎样的位置关系?25. 某电器超市销售每台进价分别为200元、170元的、两种型号的电风扇,下表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润销售收入进货成本)
(1)、求、两种型号的电风扇的销售单价;(2)、若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.26. 阅读理解:如图 , 已知点是外一点,连接 , 求的度数.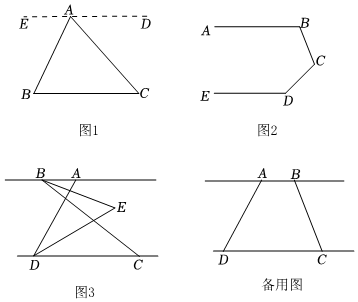 (1)、阅读并补充下面推理过程.
(1)、阅读并补充下面推理过程.解:过点作 , , .
.
.
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将 , , “凑”在一起,得出角之间的关系,使问题得以解决.
(2)、方法运用:如图2,已知 , 求的度数.(3)、深化拓展:如图3,已知 , 点在点的右侧, , 平分 , 点是直线上的一个动点(不与点重合), , 平分 , , 所在的直线交于点 , 点在与两条平行线之间.若 , 请你直接写出的度数.(用含的代数式表示).