宁夏吴忠市利通区第一共同教研体2021-2022学年九年级下学期期中考试数学试卷
试卷更新日期:2022-08-18 类型:期中考试
一、单选题
-
1. 下列运算正确的是( )A、a6÷a2=a3 B、a5﹣a3=a2 C、(3a3)2=6a9 D、2(a3b)2﹣3(a3b)2=﹣a6b22. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为( )A、 B、 C、 D、3. 如图是由7个相同的小正方体组合而成的几何体.这个几何体的左视图是( )
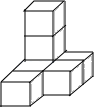 A、
A、 B、
B、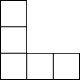 C、
C、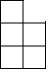 D、
D、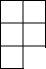 4. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:
4. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:阅读时间/小时
0.5及以下
0.7
0.9
1.1
1.3
1.5及以上
人数
2
9
6
5
4
4
则本次调查中阅读时间的中位数和众数分别是( )
A、0.7和0.7 B、0.9和0.7 C、1和0.7 D、0.9和1.15. 一副三角板如图就置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中 的度数为( )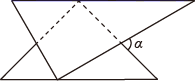 A、45° B、60° C、75° D、85°6. 如图,在四边形 中,对角线 相交于点 下列条件中能够判定这个四边形是平行四边形的是( )
A、45° B、60° C、75° D、85°6. 如图,在四边形 中,对角线 相交于点 下列条件中能够判定这个四边形是平行四边形的是( ) A、 B、 C、 D、7. 函数 和 在同一直角坐标系中的大致图象是( )A、
A、 B、 C、 D、7. 函数 和 在同一直角坐标系中的大致图象是( )A、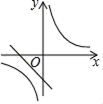 B、
B、 C、
C、 D、
D、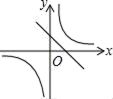 8. 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,且∠BCD=30°,CD=4 . 则图中阴影部分的面积S阴影=( )
8. 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,且∠BCD=30°,CD=4 . 则图中阴影部分的面积S阴影=( ) A、2π B、π C、π D、π
A、2π B、π C、π D、π二、填空题
-
9. 分解因式:2a3﹣8a= .10. 计算: .11. 在一个不透明的盒子里装有除颜色外其余均相同的2个黄色乒乓球和若干个白色乒乓球,从盒子里随机摸出一个乒乓球,摸到白色乒乓球的概率为 ,那么盒子内白色乒乓球的个数为.12. 已知一元二次方程3x2+4x﹣k=0有两个实数根,则k的取值范围是 .13. 如图是某校参加各兴趣小组的学生人数分布扇形统计图,已知参加 课程兴趣小组的人数为120人,则该校参加各兴趣小组的学生共有人.
 14. 如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为 .
14. 如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为 .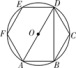 15. 如图,在等腰直角△ABC中,∠C=90°,以顶点A为圆心,适当的长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,则
15. 如图,在等腰直角△ABC中,∠C=90°,以顶点A为圆心,适当的长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,则 16. 《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图, 设门高 为 尺,根据题意,可列方程为.
16. 《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图, 设门高 为 尺,根据题意,可列方程为.
三、解答题
-
17. 解不等式组 ,并把它的解集在数轴上表示出来.18. 先化简,再求值: , 其中 .19. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,-1), B(1,-2),C(3,-3).
 (1)、将△ABC向上平移4个单位长度得到△A1B1C1 , 请画出△A1B1C1 .(2)、请画出与△ABC关于y轴对称的△A2B2C2 .(3)、请写出A1 , A2的坐标.20. 荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.(1)、求购买该品牌一个台灯、一个手电筒各需要多少元?(2)、经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?21. 某校举行冬奥会有奖知识问答活动,胡老师从全校学生的答卷中随机地抽取了部分学生的答卷进行了统计分析(卷面满分100分,且得分x均为不小于60的整数),并将竞赛成绩划分为四个等级:基本合格(60≤x<70)、合格(70≤x<80)、良好(80≤x<90)、优秀(90≤x≤100),制作了如下统计图(部分信息未给出):
(1)、将△ABC向上平移4个单位长度得到△A1B1C1 , 请画出△A1B1C1 .(2)、请画出与△ABC关于y轴对称的△A2B2C2 .(3)、请写出A1 , A2的坐标.20. 荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.(1)、求购买该品牌一个台灯、一个手电筒各需要多少元?(2)、经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?21. 某校举行冬奥会有奖知识问答活动,胡老师从全校学生的答卷中随机地抽取了部分学生的答卷进行了统计分析(卷面满分100分,且得分x均为不小于60的整数),并将竞赛成绩划分为四个等级:基本合格(60≤x<70)、合格(70≤x<80)、良好(80≤x<90)、优秀(90≤x≤100),制作了如下统计图(部分信息未给出):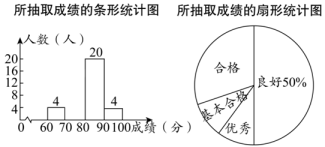
根据图中提供的信息解决下列问题:
(1)、胡老师共抽取了名学生的成绩进行统计分析,扇形统计图中“基本合格”等级对应的扇形圆心角度数为 , 请补全条形统计图.(2)、现从“优秀”等级的甲、乙、丙、丁四名学生中任选两人参加全市知识竞赛活动,请用画树形图的方法求甲学生被选到的概率.22. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF.求证:四边形OEFG是矩形 23. 如图, 是 的直径,点C是 上异于A、B的点,连接 、 ,点D在 的延长线上,且 ,点E在 的延长线上,且 .
23. 如图, 是 的直径,点C是 上异于A、B的点,连接 、 ,点D在 的延长线上,且 ,点E在 的延长线上,且 .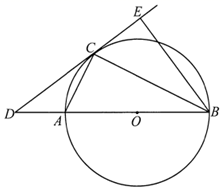 (1)、求证: 是 的切线:(2)、若 ,求 的长.24. 已知:如图,抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0).
(1)、求证: 是 的切线:(2)、若 ,求 的长.24. 已知:如图,抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0).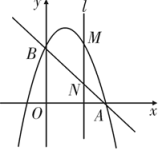 (1)、求该抛物线的函数解析式和直线AB的函数解析式;(2)、若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.25. 小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的价格w(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示.
(1)、求该抛物线的函数解析式和直线AB的函数解析式;(2)、若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.25. 小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的价格w(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示. (1)、观察图象,直接写出当0≤x≤11时,日销售量y与上市时间x之间的函数解析式为;当11≤x≤20时,日销售量y与上市时间x之间的函数解析式为 .(2)、试求出第11天的销售金额;(3)、若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的价格w元/千克将批发来的草莓全部销售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?26. 已知△AOB 的三边OA= , OB=6,AB= , 以顶点O为原点,OB所在直线为x轴建立平面直角坐标系,如图所示,点P从原点出发,以每秒1个单位长度的速度沿y轴正方向运动,设运动的时间为t秒,过点P作PN∥x轴,分别交AO,AB于点M,N,当点M与N重合时,点P停止运动.
(1)、观察图象,直接写出当0≤x≤11时,日销售量y与上市时间x之间的函数解析式为;当11≤x≤20时,日销售量y与上市时间x之间的函数解析式为 .(2)、试求出第11天的销售金额;(3)、若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的价格w元/千克将批发来的草莓全部销售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?26. 已知△AOB 的三边OA= , OB=6,AB= , 以顶点O为原点,OB所在直线为x轴建立平面直角坐标系,如图所示,点P从原点出发,以每秒1个单位长度的速度沿y轴正方向运动,设运动的时间为t秒,过点P作PN∥x轴,分别交AO,AB于点M,N,当点M与N重合时,点P停止运动. (1)、求点A的坐标,并确定t的取值范围;(2)、求MN的长度(用含t的代数式表示);(3)、设△AMN的面积为S,写出S关于t的函数关系式,并求S的最值.
(1)、求点A的坐标,并确定t的取值范围;(2)、求MN的长度(用含t的代数式表示);(3)、设△AMN的面积为S,写出S关于t的函数关系式,并求S的最值.