江苏省扬州市广陵区2021-2022学年八年级下学期期中数学试卷
试卷更新日期:2022-08-18 类型:期中考试
一、单选题
-
1. 剪纸是扬州的非物质文化遗产之一,下列剪纸作品中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,最适宜采用普查方式的是( )A、对全国初中学生视力状况的调査 B、了解江苏省义务教育阶段男女学生比例情况 C、旅客上飞机前的安全检查 D、了解某种品牌手机电池的使用寿命3. 下列统计图中,可以直观地反映出数据变化的趋势的统计图是( )A、折线图 B、扇形图 C、条形图 D、频数分布直方图4. 成语“守株待兔”所描述的事件是( )A、必然事件 B、随机事件 C、不可能事件 D、无法确定5. 无论x取什么数时,总是有意义的分式是( )A、 B、 C、 D、6. 把分式中的x和y都扩大3倍,则分式的值( )A、不变 B、扩大为原来的3倍 C、缩小为原来的 D、扩大为原来的9倍7. 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
2. 下列调查中,最适宜采用普查方式的是( )A、对全国初中学生视力状况的调査 B、了解江苏省义务教育阶段男女学生比例情况 C、旅客上飞机前的安全检查 D、了解某种品牌手机电池的使用寿命3. 下列统计图中,可以直观地反映出数据变化的趋势的统计图是( )A、折线图 B、扇形图 C、条形图 D、频数分布直方图4. 成语“守株待兔”所描述的事件是( )A、必然事件 B、随机事件 C、不可能事件 D、无法确定5. 无论x取什么数时,总是有意义的分式是( )A、 B、 C、 D、6. 把分式中的x和y都扩大3倍,则分式的值( )A、不变 B、扩大为原来的3倍 C、缩小为原来的 D、扩大为原来的9倍7. 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( ) A、75° B、60° C、55° D、45°8. 如图,在▱ABCD中,AD=2AB , F是AD的中点,作CE⊥AB , 垂足E在线段AB上,连接EF、CF , 下列结论中:①∠DCF= ∠BCD;②∠DFE=3∠AEF;③EF=CF;④S△BEC=S△CEF . 一定成立的是( )
A、75° B、60° C、55° D、45°8. 如图,在▱ABCD中,AD=2AB , F是AD的中点,作CE⊥AB , 垂足E在线段AB上,连接EF、CF , 下列结论中:①∠DCF= ∠BCD;②∠DFE=3∠AEF;③EF=CF;④S△BEC=S△CEF . 一定成立的是( ) A、①②③④ B、①②③ C、①②④ D、①③④
A、①②③④ B、①②③ C、①②④ D、①③④二、填空题
-
9. 为了解新冠肺炎疫情解封后刚复学时学生的心理健康,扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查,对500个数据进行整理,在频数的统计表中各组的频数之和等于 .10. 样本的50个数据分别落在4个组内,第1、2、3组数据的个数分别是7、8、15,则落在第4组数据的频数为 .11. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
 12. 若分式的值为负数,则x的取值范围是 .13. 如果 , 则= .14. 如图,▱ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为.
12. 若分式的值为负数,则x的取值范围是 .13. 如果 , 则= .14. 如图,▱ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为. 15. 已知菱形的周长为20,一条对角线长为8,则菱形的面积为 .16. 如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠C′AB′的度数为 .
15. 已知菱形的周长为20,一条对角线长为8,则菱形的面积为 .16. 如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠C′AB′的度数为 .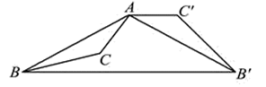 17. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .
17. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .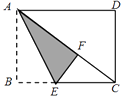 18. 如果记=f(x),并且f(1)表示当x=1时y的值,即f(1)=;f()表示,当x=时y的值,即f()=;那么f(1)+f(2)+f()+f(3)+f()+…+f(2021)+f()+f(2022)+f()= .
18. 如果记=f(x),并且f(1)表示当x=1时y的值,即f(1)=;f()表示,当x=时y的值,即f()=;那么f(1)+f(2)+f()+f(3)+f()+…+f(2021)+f()+f(2022)+f()= .三、解答题
-
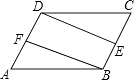
19. 如图,平行四边形ABCD中,E、F分别是边BC、AD的中点,求证:∠ABF=∠CDE.
 20. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
20. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:摸球的次数
100
200
300
500
800
1000
3000
摸到白球的次数
65
124
178
302
481
599
1803
摸到白球的频率
0.65
0.62
0.59
0.604
0.601
0.599
0.601
(1)、请估计:当n很大时,摸到白球的频率将会接近(精确到0.1)(2)、假如你摸一次,你摸到白球的概率P(白球)= .(3)、试估算盒子里黑、白两种颜色的球各有多少只?21. 扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.
根据以上信息,回答下列问题:
(1)、本次调查的样本容量是 , 扇形统计图中表示A等级的扇形圆心角为 ;(2)、补全条形统计图;(3)、学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.22. 如图,在正方形网格中,△AOB的顶点均在格点上点A、B的坐标分别是A(3,2)、B(1,3).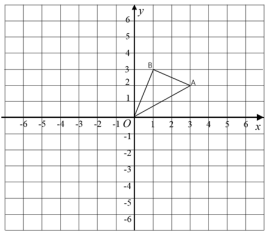 (1)、点A关于点O中心对称点的坐标为;(2)、△AOB绕点O顺时针旋转90°后得到△A1OB1 , 在方格纸中画出△A1OB1 , 并写出点B1的坐标 ▲ ;(3)、在y轴上找一点P,使得PA+PB最小,请在图中标出点P的位置,并求出这个最小值.23. 已知:如图,E、F是▱ABCD的对角线AC上的两点,AE=CF.
(1)、点A关于点O中心对称点的坐标为;(2)、△AOB绕点O顺时针旋转90°后得到△A1OB1 , 在方格纸中画出△A1OB1 , 并写出点B1的坐标 ▲ ;(3)、在y轴上找一点P,使得PA+PB最小,请在图中标出点P的位置,并求出这个最小值.23. 已知:如图,E、F是▱ABCD的对角线AC上的两点,AE=CF.求证:
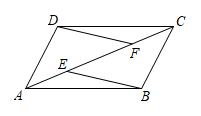 (1)、△ADF≌△CBE;(2)、EB∥DF.24. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE.
(1)、△ADF≌△CBE;(2)、EB∥DF.24. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE. (1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.25. 在 ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.25. 在 ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.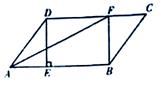 (1)、求证:四边形BFDE是矩形;(2)、若CF=3,BF=4,DF=5,求证:AF平分∠DAB.26. 阅读下面材料:
(1)、求证:四边形BFDE是矩形;(2)、若CF=3,BF=4,DF=5,求证:AF平分∠DAB.26. 阅读下面材料:在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗.
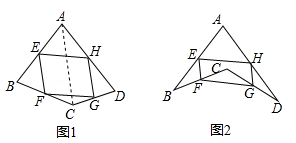
小敏在思考问题时,有如下思路:连接AC.
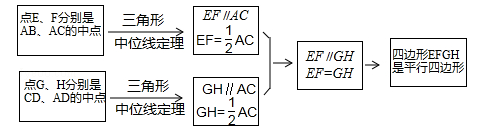
结合小敏的思路作答:
(1)、若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;(2)、如图2,在(1)的条件下,若连接AC,BD.①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
27. 在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知: ,求代数式x2+ 的值.
解:∵ ,∴ =4
即 =4∴x+ =4∴x2+ =(x+ )2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求 的值.
解:令2x=3y=4z=k(k≠0)
则
根据材料回答问题:
(1)、已知 ,求x+ 的值.(2)、已知 ,(abc≠0),求 的值.(3)、若 ,x≠0,y≠0,z≠0,且abc=7,求xyz的值.28.(1)、【方法回顾】
如图1,过正方形ABCD的顶点A作一条直线l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,若DF=2.5,BE=1,则EF= .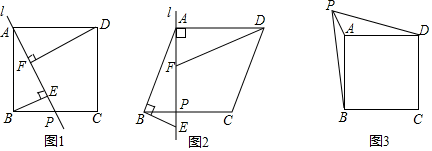 (2)、【问题解决】
(2)、【问题解决】
如图2,菱形ABCD的边长为1.5,过点A作一条直线l交边BC于点P,且∠DAP=90°,点F是AP上一点,且∠BAD+∠AFD=180°,过点B作BE⊥AB,与直线l交于点E,若EF=1,求BE的长.(3)、【思维拓展】
如图3,在正方形ABCD中,点P在AD所在直线上的上方,AP=2,连接PB,PD,若△PAD的面积与△PAB的面积之差为m(m>0),则PB2﹣PD2的值为 . (用含m的式子表示)