江苏省无锡市惠山区2021-2022学年九年级下学期期中数学试卷
试卷更新日期：2022-08-18 类型：期中考试
一、单选题
-
1. 一5的绝对值是（ ）A、5 B、 C、 D、－52. 函数y＝中自变量x的取值范围是（ ）A、x＞7 B、x＜7 C、x≥7 D、x≠73. 一组数据：2， ， 0，3， ， 2，则这组数据的中位数和众数分别是（ ）A、1.5，2 B、1，2 C、0，2 D、1，34. 下列运算中，结果正确的（ ）A、（a﹣1）（a+1）＝a2﹣1 B、+＝ C、（a+b）2＝a2+b2 D、a6÷a2＝a35. 每年3月21日是世界睡眠日，良好的睡眠状况是保持身体健康的重要基础．为了解某校800名初三学生的睡眠时间，从13个班级中抽取50名学生进行调查，下列说法正确的是（ ）A、800名学生是总体 B、50是样本容量 C、13个班级是抽取的一个样本 D、每名学生是个体6. 下列四个有关环保的图形中，是轴对称图形，但不是中心对称图形的是（ ）A、
B、
C、
D、
7. 如图，四边形ABCD为⊙O的内接四边形，若∠A＝50°，则∠BCD的度数为（ ）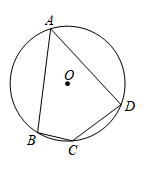
A、50° B、80° C、100° D、130°8. 下列性质中，菱形具有而矩形不一定具有的是（ ）A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边互相垂直9. 如图，直线y=x－2与y轴交于点C，与x轴交于点B，与反比例函数的图象在第一象限交于点A，连接OA，若S△AOB：S△BOC = 1∶2，则k的值为（ ）
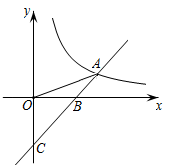A、2 B、3 C、4 D、610. 我们定义：两边平方和等于第三边平方的2倍的三角形叫做奇异三角形，根据定义：①等边三角形一定是奇异三角形；②在Rt△ABC中，∠C＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若Rt△ABC是奇异三角形，则a：b：c＝1：：2；③如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE＝AD，CB＝CE．则△ACE是奇异三角形；④在③的条件下，当△ACE是直角三角形时，∠AOC＝120°，其中，说法正确的有（ ）
A、①② B、①③ C、②④ D、③④二、填空题
-
11. 分解因式：ax2﹣6ax+9a= ．12. 化简 ．13. “学中共党史，庆建党百年”，截至4月26日，某市党员群众参与答题次数达8420000次，掀起了党史学习竞赛的热潮，数据“8420000”用科学记数法可表示为 ．14. 某圆锥的母线长是2，底面半径是1，则该圆锥的侧面积是 ．15. 请写出一个函数表达式，使其图象的对称轴为 轴：.16. 如图所示的网格是由相同的小正方形组成的网格，点A，B，P是网格线的交点，则∠PAB＋∠PBA＝ ．
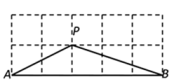
17. 如图，线段AB＝10，点D是线段AB上的一个动点（不与点A重合），在AB上方作以AD为腰的等腰△ACD，且∠CAD＝120°，过点D作射线DP⊥CD，过DP上一动点G（不与D重合）作矩形CDGH，其对角线交点为O，连接OB，则线段OB的最小值为 ．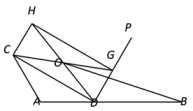
18. 如图，在平面直角坐标系中，抛物线y＝－（x＋m）2＋m2－m的顶点为A，与y轴交于点B，则点B的坐标为（用含m的代数式表示）；若作AC⊥AB，且∠ABC＝∠ABO（C、O在AB的两侧），设点C的坐标为（x，y），则y关于x的函数关系式为 ．
三、解答题
-
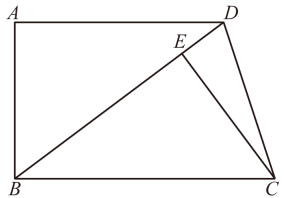
19.(1)、计算：sin45°－（π－4）0(2)、化简：（1＋a）（1－a）＋a（a－2）．20.(1)、解方程：x2-4x-1=0；(2)、解不等式组：21. 如图，在四边形ABCD中，AD//BC，BC＝BD，点E在BD上，∠A＝∠BEC＝90°．
(1)、求证：△ABD≌△ECB；(2)、若AD＝4，CE＝3，求CD的长．22. 小明参加某网店的“翻牌抽奖”活动，如图，4张牌分别对应价值为5元，10元，15元和20元的4件奖品．
(1)、如果随机翻1张牌，则抽中价值为20元的奖品的概率为；(2)、如果随机翻2张牌，且第一次翻过的牌不再参加下次翻牌，求所获奖品总价值不低于30元的概率．（请用“画树状图”或“列表”法写出分析的过程）23. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图，请根据相关信息，解答下列问题：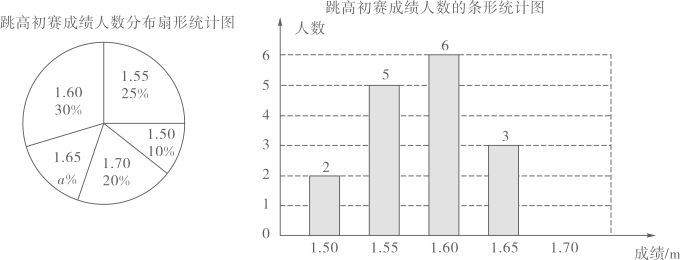
(1)、扇形统计图中，初赛成绩为1.65m所在扇形的圆心角为°；(2)、补全条形统计图；(3)、根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？24. 如图，矩形ABCD中，AD＞AB，（如需画草图，请使用备用图）
(1)、请用无刻度的直尺和圆规按下列要求作图：（不写作法，保留作图痕迹）①在BC边上取一点E，使AE＝BC；
②在CD上作一点F，使点F到点D和点E的距离相等．
(2)、在（1）中，若AB＝6，AD＝10，则△AEF 的面积＝ ．25. 如图，AB为⊙O的直径，C为BA延长线上一点，CD与⊙O相切于点D．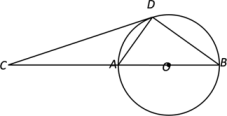
(1)、求证：△CAD∽△CDB；(2)、若sinC＝ ， BD＝6，求⊙O的半径．26. 据环保中心观察和预测：发生于甲地的河流污染一直向下游方向移动，其移动速度v（千米/小时）与时间t（小时）的函数图象如图所示，过线段OC上一点T（t，0）作横轴的垂线l，根据物理知识：梯形OABC在直线l左侧部分的面积表示的实际意义为t（小时）内污染所经过的路程S（千米），其中0≤t≤30．
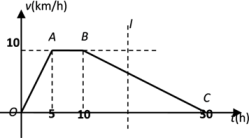(1)、当t＝3时，则S的值为；(2)、求S与t的函数表达式；(3)、若乙城位于甲地的下游，且距甲地171千米，试判断这河流污染是否会侵袭到乙城？若会，求河流污染发生后多长时间它将侵袭到乙城；若不会，请说明理由．27. 在平面直角坐标系中，抛物线y＝ax2＋bx＋c与y轴交于点A（0，4）、与x轴交于点B（2，0）和点C（－1，0）．
(1)、求抛物线的函数表达式；(2)、若点D为第一象限的抛物线上一点，①过点D作DE⊥AB，垂足为点E，求线段DE长的取值范围；
②若点F、G分别为线段OA、AB上一点，且四边形AFGD既是中心对称图形，又是轴对称图形，求此时点D的坐标．
28.(1)、【操作发现】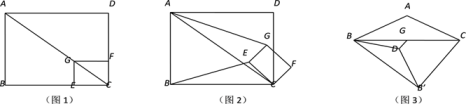
如图1，在矩形ABCD和矩形CEGF中，＝ ， AB＝9，AD＝12，小明将矩形CEGF绕点C顺时针转一定的角度，如图2所示．
①问：的值是否变化？若不变，求的值；若变化，请说明理由．
②在旋转过程中，当点B、E、F在同一条直线上时，求AG的长度．
(2)、【类比探究】如图3，在△ABC中，AB＝AC＝2 ， ∠BAC＝α°，tan∠ABC＝ ， G为BC中点，点D为平面内一动点，且DG＝ ， 将线段BD绕点D逆时针旋转α°得到DB′，则四边形BACB′面积的最大值为 ．