湖北省武汉市青山区2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-08-18 类型：期中考试

进入出卷网下载

一、单选题

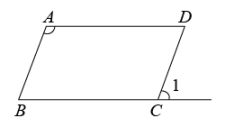
1. 若 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x＞0 B、x＞2 C、x≥2 D、x≤2

查看试题解析
2. 以下列各组数为边长，能构成直角三角形的是（）

A、1，2，3 B、2，3，4 C、2，2，5 D、2， $\sqrt{5}$ ， 3

查看试题解析
3. 若 $\sqrt{a}$ 是最简二次根式，则a的值可能是（）

A、2 B、4 C、-3 D、1.5

查看试题解析
4. 如图，在▱ABCD中，∠A=110°，则∠1的度数为（）

A、70° B、65° C、60° D、110°

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\frac{\sqrt{18} - \sqrt{8}}{2} = \sqrt{9} - \sqrt{4}$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$

查看试题解析
6. 正方形具有而矩形不一定具有的性质是（）

A、四个角都相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直

查看试题解析
7. 已知 $x = 2 + \sqrt{3}$ ，则代数式 $x^{2} - 4 x + 3$ 的值为（）

A、2 B、6 C、4 D、 $\sqrt{3}$

查看试题解析
8. 如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB于点E，若∠ADC=130°，则∠AOE的大小为（）

A、75° B、65° C、55° D、50°

查看试题解析
9. 如图，在Rt△ABC中∠ACB=90°，∠A=30°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF= $\frac{1}{2}$ BC，若EF=4，则DE的长为（）

A、4 B、 $\sqrt{3} + 1$ C、2 D、 $\sqrt{3}$

查看试题解析
10. 如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，分别以AB，AC，BC为边向△ABC外作正方形ABED，正方形ACHI，正方形BCGF．直线ED，HI交于点J，过点F作KF // HI，交DE于点K，过点G作GM // DE，与HI，KF分别交于点M，L. 则四边形KLMJ的面积为（）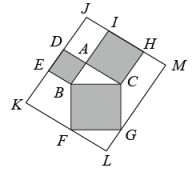

A、90 B、100 C、110 D、120

查看试题解析

二、填空题

11. 计算： $\sqrt{{(- 3)}^{2}}$ = ．

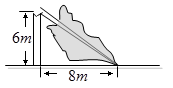
查看试题解析
12. 如图由于台风的影响，一棵树在离地面 $6 m$ 处折断，树顶落在离树干底部 $8 m$ 处，则这棵树在折断前（不包括树根）长度是．

查看试题解析
13. 如图，在▱ABCD两对角线A，BD相交于点O，且AC+BD=36，AB=11，则△COD的周长是．

查看试题解析
14. 如果 $\sqrt{28 n}$ 是整数，则正整数n的最小值是

查看试题解析
15. 如图，在矩形ABCD中，AD= $\sqrt{2}$ AB，∠BAD的平分线交BC于点E，过D作AE的垂线，垂足为点.H，连接BH并延长，交CD于点F，连接DE交BF于点O，则下列结论：①△ABE≌△AHD；②∠AED=∠CED；③BH=FH；④CD=FH；⑤BC－CF=HE，其中正确的是．（填序号）

查看试题解析
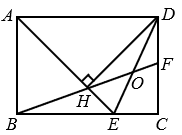16. 如图，正方形ABCD的边长为6，点P为BC边上一动点，以P为直角顶点，AP为直角边作等腰Rt△APE，M为边AE的中点，当点P从点B运动到点C，则点M运动的路径长为．

查看试题解析

三、解答题

17. 计算：
（1） $\sqrt{12} - 3 \sqrt{\frac{1}{3}} + \sqrt{3}$

查看试题解析
18. 如图，在△ABC中，AB=13，BC=12，AC=5，点D是BC上一点，且CD=3．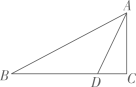

(1)、试判断△ABC的形状，并说明理由；

(2)、求AD的长．

查看试题解析
19. 如图，▱ABCD的对角线AC，BD相交于点O，点E、F在AC上，且AF=CE．
求证：BE=DF．

查看试题解析
20. 如图，在正方形ABCD中，点E为边AD中点. 用无刻度直尺画出以下图形，画图过程用虚线表示，画图结果用实线表示．

(1)、在边BC上找点F使直线EF平分正方形ABCD的面积；

(2)、画出边AB的中点N；

(3)、在边CD上找点Q使AQ⊥BE；

(4)、在直线BC上找点P使DP // CE．

查看试题解析
21. 如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作BC的垂线，垂足为点E，延长BC到点F，使CF=BE，连接DF．

(1)、求证：四边形AEFD是矩形；

(2)、连接OE，若AB=13，OE=5，求AE的长．

查看试题解析
22. 如图，一架梯子AB斜靠在某个走廊竖直的左墙上，顶端在点A处，底端在水平地面的点B处. 保持梯子底端B的位置不变，将梯子斜靠在竖直的右墙上，此时梯子的顶端在点E处．

(1)、如图1，若顶端A距离地面的高度AC为2.4米，BC为0.7米．
①则梯子的长为 ▲ 米；

②若顶端E距离地面的高度EF比AC少0.4米，求走廊的宽是多少米?

(2)、如图2，G是线段AE上中点左侧一点，若BG=2，AC•GE= $2 \sqrt{3}$ ，则梯子的长为米．

查看试题解析
23. 在 $▱$ ABCD中，点E是AB的中点，点P是BC上一点，连接DE，交AP于点M．N是AP上一点，且AM=MN，连接BN并延长交DC于点F．

(1)、如图1，求证：四边形EBFD是平行四边形；

(2)、如图2，连接MC交BF于点H，过点A作AG $//$ MC交DE于点G．
①求证：MC=2AG；

②当点P为BC中点时，若BF=a，AP=b，且 $\frac{25}{4} A B^{2} = a^{2} + 4 b^{2}$ ，直接写出相应的 $▱$ ABCD的面积（用含a，b的式子表示）．

查看试题解析
24. 如图，点B（m，n）为平面直角坐标系内一点，且m，n满足 $n = \sqrt{m - 6} + \sqrt{6 - m} + 6$ ，过点B分别作BA⊥y轴于点A，BC⊥x轴于点C．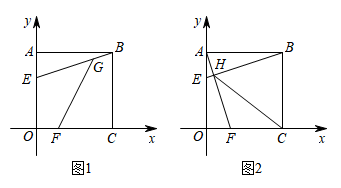

(1)、求证：四边形ABCO是正方形；

(2)、点E（0，b）为y轴上一点，点F（a，0）为x轴上一点．
①如图1，若a=2，b=4，点G为线段BE上一点，且∠EGF=45°，求线段FG的长；

②如图2，若a+b=6，直线AF与BE交于点H，连接CH，则CH的最小值为 ▲ ．

查看试题解析