江苏省扬州市江都区邵樊片2021-2022学年八年级下学期期中数学试卷
试卷更新日期:2022-08-18 类型:期中考试
一、单选题
-
1. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列代数式是分式的是( )A、 B、 C、 D、3. 下列命题中正确的是( )A、有一组邻边相等的四边形是菱形 B、有一个角是直角的四边形是矩形 C、对角线互相垂直的平行四边形是正方形 D、对角线互相平分的四边形是平行四边形4. 为了解参加运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄.就这个问题来说,下面说法中正确的是( )A、抽取的100名运动员的年龄是样本 B、2000名运动员是总体 C、100名运动员是抽取的一个样本容量 D、每个运动员是个体5. 如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )
2. 下列代数式是分式的是( )A、 B、 C、 D、3. 下列命题中正确的是( )A、有一组邻边相等的四边形是菱形 B、有一个角是直角的四边形是矩形 C、对角线互相垂直的平行四边形是正方形 D、对角线互相平分的四边形是平行四边形4. 为了解参加运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄.就这个问题来说,下面说法中正确的是( )A、抽取的100名运动员的年龄是样本 B、2000名运动员是总体 C、100名运动员是抽取的一个样本容量 D、每个运动员是个体5. 如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=118°,则∠BCE=( )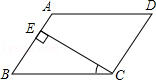 A、28° B、38° C、62° D、72°6. 已知 , 则代数式的值为( )A、3 B、﹣2 C、﹣ D、﹣7. 某工程队准备修建一条长1200米的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前两天完成任务,若设原计划每天修建道路x米,则根据题意可列方程为( ).A、 B、 C、 D、8. 如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=( )
A、28° B、38° C、62° D、72°6. 已知 , 则代数式的值为( )A、3 B、﹣2 C、﹣ D、﹣7. 某工程队准备修建一条长1200米的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前两天完成任务,若设原计划每天修建道路x米,则根据题意可列方程为( ).A、 B、 C、 D、8. 如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=( )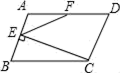 A、54° B、60° C、66° D、72°
A、54° B、60° C、66° D、72°二、填空题
-
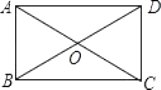
9. 样本的50个数据分别落在4个组内,第1、2、3组数据的个数分别是7、8、15,则落在第4组数据的频数为 .10. 分式与的最简公分母是 .11. 若 ,则 .12. 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为 .
 13. 如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长等于cm.
13. 如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长等于cm.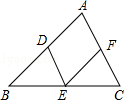 14. 当时,分式的值是 .15. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,DE⊥BC,垂足为点E,则DE= .
14. 当时,分式的值是 .15. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,DE⊥BC,垂足为点E,则DE= .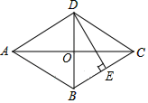 16. 若关于x的分式方程=2的解为正数,则m的取值范围是 .17. 如图,在平面直角坐标系中,平行四边形的边落在x轴的正半轴上,且点 , , 直线平分平行四边形的面积,则 .
16. 若关于x的分式方程=2的解为正数,则m的取值范围是 .17. 如图,在平面直角坐标系中,平行四边形的边落在x轴的正半轴上,且点 , , 直线平分平行四边形的面积,则 .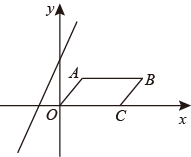 18. 如图,正方形和正方形的边长分别为4和2,正方形绕点C旋转,则 .
18. 如图,正方形和正方形的边长分别为4和2,正方形绕点C旋转,则 .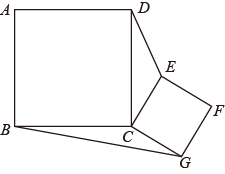
三、解答题
-
19.(1)、计算:(2)、20.(1)、解方程:(2)、;21. 先化简,再求值: ,其中 满足 .22. 为了检查“防震减灾”落实情况,我市教育部门对一中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级;小明根据调查结果绘制了如下统计图,请根据提供的信息回答问题:
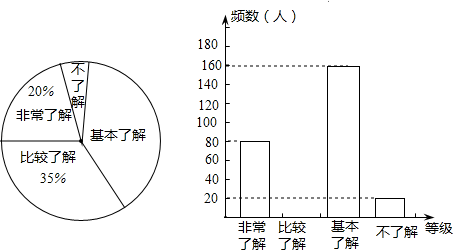 (1)、本次参与问卷调查的学生有人:扇形统计图中“基本了解”部分所对应的扇形圆心角是度;(2)、请补全频数分布直方图;(3)、该校有2500名学生,估计对防震减灾“不了解”的人数有 .23. 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,在建立平面直角坐标系后,点C的坐标为(-2,-2).
(1)、本次参与问卷调查的学生有人:扇形统计图中“基本了解”部分所对应的扇形圆心角是度;(2)、请补全频数分布直方图;(3)、该校有2500名学生,估计对防震减灾“不了解”的人数有 .23. 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,在建立平面直角坐标系后,点C的坐标为(-2,-2).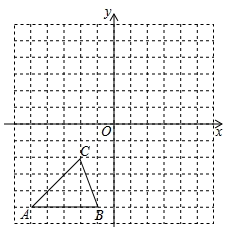
(1)画出△ABC以y轴为对称轴的对称图形 , 并写出点C1的坐标;
(2)以原点O为对称中心,画出关于原点O对称的并写出点C2的坐标;
(3)以C2为旋转中心,把顺时针旋转90°,得到△C2A3B3 .24. 如图,点E、F在线段BC上,AB=CD,BE=CF且∠B=∠C.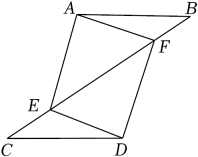 (1)、求证:△ABF≌△DCE;(2)、请猜想四边形AEDF的形状,并加以证明.25. 某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.(1)、求每个甲种配件、每个乙种配件的价格分别为多少万元;(2)、现投入资金40万元,根据维修需要预测,甲种配件要比乙种配件至少要多11件,问乙种配件最多可购买多少件.26. 阅读下面的解题过程:
(1)、求证:△ABF≌△DCE;(2)、请猜想四边形AEDF的形状,并加以证明.25. 某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.(1)、求每个甲种配件、每个乙种配件的价格分别为多少万元;(2)、现投入资金40万元,根据维修需要预测,甲种配件要比乙种配件至少要多11件,问乙种配件最多可购买多少件.26. 阅读下面的解题过程:已知 ,求 的值.
解:由 知 所以 即
所以, 所以 的值为 .
说明:该题的解法叫做“倒数法
请你利用“倒数法”解下面题目:
已知: 求:
(1)、 的值;(2)、 的值。27. 如图,在平面直角坐标系中,点O为坐标原点,AB∥OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.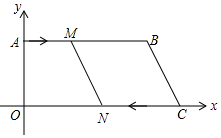 (1)、在t=3时,M点坐标 , N点坐标 ;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.28. 知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
(1)、在t=3时,M点坐标 , N点坐标 ;(2)、当t为何值时,四边形OAMN是矩形?(3)、运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.28. 知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.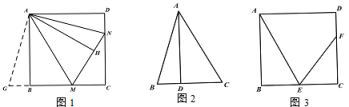 (1)、知识探究:在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;(2)、知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为;(3)、知识拓展:如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.
(1)、知识探究:在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;(2)、知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为;(3)、知识拓展:如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.