江苏省扬州市江都区八校2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-08-18 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列成语描述的事件为随机事件的是（）

A、猴子捞月 B、水涨船高 C、守株待兔 D、旭日东升

查看试题解析
3. 菱形具有而矩形不一定具有的性质是（）

A、两组对边分别平行 B、对角线相等 C、对角线互相垂直 D、两组对边分别相等

查看试题解析
4. 一组数据的最大值为105，最小值为23，若确定组距为9，则分成的组数为（）

A、11 B、10 C、9 D、8

查看试题解析
5. 如果分式 $\frac{2 x y}{3 x - 3 y}$ 中，x，y的值都变为原来的2倍，则分式的值（）

A、不变 B、缩小为原来的 $\frac{1}{2}$ C、扩大2倍 D、不能确定

查看试题解析
6. 如图，菱形ABCD的对角线AC，BD相交于点O， $A C = 8$ ， $B D = 6$ ，点E为BC的中点，则OE的长为（）

A、2.5 B、3 C、5 D、6

查看试题解析
7. 如图，在直角坐标系中，正方形ABCD如图摆放，若顶点A，B的坐标分别为 $(a ， 0)$ ， $(0 ， b)$ ，则顶点D的坐标为（）

A、 $(- b ， a + b)$ B、 $(a - b ， - a)$ C、 $(- a ， a - b)$ D、 $(b - a ， - a)$

查看试题解析
8. 如图，在△ABC中，∠BAC＝90°，AB＝6，AC＝8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则PM的最小值为（　　）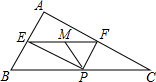

A、5 B、2.5 C、4.8 D、2.4

查看试题解析

二、填空题

9. 化简 $\frac{a^{2} - 4}{a + 2}$ 的结果是．

查看试题解析
10. 已知数据： $\frac{1}{2}$ ， $\sqrt{5}$ ，π， $\sqrt{4}$ ，0，其中无理数出现的频率为.

查看试题解析
11. 当 $x =$ 时，分式 $\frac{x^{2} - 1}{(x - 3) (x - 1)}$ 的值为零

查看试题解析
12. 如图，点D、E分别为 $△ A B C$ 的边AB、AC的中点．连接DE，过点B作BF平分 $∠ A B C$ ，交DE于点F．若 $E F = 4$ ， $A D = 7$ ，则BC的长为．

查看试题解析
13. 若 $\frac{1}{a} - \frac{1}{b} = 3$ ，则分式 $\frac{2 a + 3 a b - 2 b}{a - 2 a b - b} =$ ﹒

查看试题解析
14. 点E、F、G、H分别是任意四边形ABCD中AD、AB、BC、CD各边的中点，对角线AC，BD交于点O，当四边形ABCD满足条件时，四边形EFGH是菱形．

查看试题解析
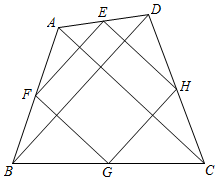15. 如图，E、F分别是平行四边形ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q，若 $S_{△ A P D} = 17 c m^{2}$ ， $S_{△ B Q C} = 27 c m^{2}$ ，则阴影部分的面积为

查看试题解析
16. 如图，在菱形ABCD中，∠A＝120°，AB＝2，点E为BC的中点，P为对角线BD上的一个动点，分别连接PE、PC，则PE+PC的最小值＝．

查看试题解析
17. 如图，已知 $△ A B C$ 中， $A B = A C ， ∠ B A C = 90 °$ ，直角 $∠ E P F$ 的顶点P是 $B C$ 的中点，两边 $P E$ 、 $P F$ 分别交 $A B$ 、 $A C$ 于点E、F，给出以下四个结论：
① $A E = C F$ ；
② $△ E P F$ 是等腰直角三角形；
③ $S_{四边形 A E P F} = \frac{1}{2} S_{△ A B C}$ ；
④当 $∠ E P F$ 在 $△ A B C$ 内绕顶点P旋转时（点E不与A、B重合）， $B E + C F = E F$ ．
上述结论中始终正确的有（填序号）．

查看试题解析
18. 如图，在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点B （6，2），C（4，0）直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移，经过秒该直线可将平行四边形OABC分成面积相等的两部分.

查看试题解析

三、解答题

19. 计算：

(1)、 $\frac{a^{2}}{a + 3} \div \frac{6 a}{a^{2} - 9}$

(2)、 $\frac{a^{2} + a}{a^{2} - 2 a + 1} \div (\frac{2}{a - 1} - \frac{1}{a})$

查看试题解析
20. 2020年5月5日18时，我国载人空间站研制的长征五号B运载火箭在海南文昌首飞成功，正式拉开我国载人航天工程“第三步”任务的序幕．某校为了解学生对我国航天事业的关注程度，随机抽取了部分学生进行问卷测试（测试满分100分，得分x均为不小于60的整数），并将测试成绩分为四个等级：基本合格 $(60 \leq x < 70)$ ，合格 $(70 \leq x < 80)$ ，良好 $(80 \leq x < 90)$ ，优秀 $(90 \leq x < 100)$ ，制作了如图所示的统计图（部分信息未给出）．
由图中给出的信息解答下列问题：

(1)、本次调查抽取了名学生；

(2)、补全频数分布直方图；

(3)、求扇形统计图中“良好”所对应的扇形圆心角的度数；

(4)、若全校共有学生1800人，请你估计有多少名学生对我国航天事业的关注程度能达到良好及以上等级．

查看试题解析
21. 先化简，再求值： $(\frac{1}{x + 1} - 1) \div \frac{x^{2} - x}{x + 1}$ ，其中x是﹣1、1、2中的一个合适的数．

查看试题解析
22. 如图，在平面直角坐标系中， $R t Δ A B C$ 的三个顶点分别是 $A (- 3 ， 2)$ ， $B (0 ， 4)$ ， $C (0 ， 2)$ ．

(1)、将△ABC绕C点旋转180°，作出旋转后对应的△A₁B₁C₁；

(2)、平移△ABC到△A₂B₂C₂ ，使点A的对应点A₂的坐标为（﹣1，﹣4）；

(3)、若将△A₁B₁C₁绕某一点旋转可以得到△A₂B₂C₂ ，则该旋转中心的坐标为．

查看试题解析
23. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，表格是活动进行中的一组统计数据：
摸球的次数n
100
200
300
500
800
1000
摸到黑球的次数m
65
118
189
310
482
602
摸到黑球的频率 $\frac{m}{n}$
0.65
0.59
0.63
0.62
0.603
0.602

(1)、请估计：当n很大时，摸到黑球的频率将会接近（精确到0.1）；

(2)、试估计袋子中有黑球个；

(3)、若学习小组通过实验结果，想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%，则可以在袋子中增加相同的白球个．

查看试题解析
24. 如图，在四边形ABCD中，AD∥BC，BA＝BC，BD平分∠ABC．

(1)、求证：四边形ABCD是菱形；

(2)、连接AC，过点D作DE∥AC，交BC的延长线于点E，若BC＝5，BD＝8，求ED的长．

查看试题解析
25. 如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．

(1)、求证：AD=AF；

(2)、当△ABC满足什么条件时，四边形ADCF是矩形．并说明理由．

查看试题解析
26. 观察下列等式：
第1个等式： $1 + \frac{1}{1 \times 3} = \frac{2^{2}}{1 \times 3}$ ；

第2个等式： $1 + \frac{1}{2 \times 4} = \frac{3^{2}}{2 \times 4}$ ；

第3个等式： $1 + \frac{1}{3 \times 5} = \frac{4^{2}}{3 \times 5}$ ；

第4个等式： $1 + \frac{1}{4 \times 6} = \frac{5^{2}}{4 \times 6} \cdot \cdot \cdot \cdot \cdot \cdot$

按照以上规律，解决下列问题；

(1)、写出第5个等式：；

(2)、写出第n个等式：（用含n的等式表示），并证明；

(3)、计算： $(1 + \frac{1}{1 \times 3}) \times (1 + \frac{1}{2 \times 4}) \times (1 + \frac{1}{3 \times 5}) \times (1 + \frac{1}{4 \times 6}) \times \cdot \cdot \cdot \times (1 + \frac{1}{2020 \times 2022}) \times (1 + \frac{1}{2021 \times 2023})$

查看试题解析
27. 如图，矩形ABCD中，AB=4，∠ADB=30°．一动点P从B点出发沿对角线BD方向以每秒2个单位长度的速度向点D匀速运动，同时另一动点Q从D点出发沿从DC方向以每秒1个单位长度的速度向点C匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点P、Q运动的时间为t秒（t>0）．过点P作PE⊥BC于点E，连接EQ，PQ．

(1)、求证：PE=DQ；

(2)、四边形PEQD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．

(3)、当t为何值时，△PQE为直角三角形？请说明理由．

查看试题解析
28. 如图1，点O是正方形ABCD两对角线的交点. 分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．

(1)、求证：DE⊥AG；

(2)、正方形ABCD固定，将正方形OEFG绕点O逆时针旋转 $α$ 角（0°< $α$ <360°）得到正方形 $O E' F' G'$ ，如图2．
①在旋转过程中，当∠ $O A G'$ 是直角时，求 $α$ 的度数；（注明：当直角边为斜边一半时，这条直角边所对的锐角为30度）
②若正方形ABCD的边长为1，在旋转过程中，求 $A F'$ 长的最大值和此时 $α$ 的度数，直接写出结果不必说明理由．

查看试题解析

摸球的次数n	100	200	300	500	800	1000
摸到黑球的次数m	65	118	189	310	482	602
摸到黑球的频率 $\frac{m}{n}$	0.65	0.59	0.63	0.62	0.603	0.602