江苏省苏州市西安交通大学苏州附属初级中学2021-2022学年八年级下学期期中数学试卷
试卷更新日期:2022-08-18 类型:期中考试
一、单选题
-
1. 下列方程中,属于一元二次方程的是( )A、x2+3y=1 B、x2+3x=1 C、ax2+bx+c=2 D、2. 图①是苏州园林内的一种窗棂,图②是这种窗棂中的部分图案,该图案是由1个正六边形和6个全等的等边三角形组成的,则该图案( )
 A、既不是轴对称图形也不是中心对称图形 B、是中心对称图形但并不是轴对称图形 C、是轴对称图形但并不是中心对称图形 D、既是轴对称图形又是中心对称图形3. 若关于x的一元二次方程 的一个解是 ,则 的值是( )A、2025 B、2015 C、2021 D、20194. 下列关于反比例函数的描述,正确的是( )A、它的图象经过点( , 4) B、图象的两支分别在第二、四象限 C、当x>2时,0<y<4 D、x>0时,y随x的增大而增大5. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、6. 如图,已知四边形 是平行四边形,对角线 交于点 ,则下列结论中错误的是( )
A、既不是轴对称图形也不是中心对称图形 B、是中心对称图形但并不是轴对称图形 C、是轴对称图形但并不是中心对称图形 D、既是轴对称图形又是中心对称图形3. 若关于x的一元二次方程 的一个解是 ,则 的值是( )A、2025 B、2015 C、2021 D、20194. 下列关于反比例函数的描述,正确的是( )A、它的图象经过点( , 4) B、图象的两支分别在第二、四象限 C、当x>2时,0<y<4 D、x>0时,y随x的增大而增大5. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、6. 如图,已知四边形 是平行四边形,对角线 交于点 ,则下列结论中错误的是( )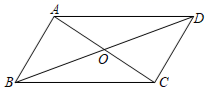 A、当 时,它是菱形 B、当 时,它是正方形 C、当 时,它是矩形 D、当 时,它是菱形7. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且8. 如图,正方形ABCD和▱AEFC,点B在EF边上,若正方形ABCD和▱AEFC的面积分别是S1、S2的大小关系是( )
A、当 时,它是菱形 B、当 时,它是正方形 C、当 时,它是矩形 D、当 时,它是菱形7. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且8. 如图,正方形ABCD和▱AEFC,点B在EF边上,若正方形ABCD和▱AEFC的面积分别是S1、S2的大小关系是( ) A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定9. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、
A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定9. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、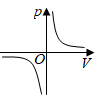 B、
B、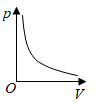 C、
C、 D、
D、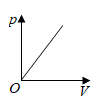 10. 如图,两个正方形的边长都为6,其中正方形 绕着正方形 的对角线的交点 旋转,正方形 与边 、 分别交于点 、 (不与端点重合),设两个正方形重叠部分形成图形的面积为 , 的周长为 ,则下列说法正确的是( )
10. 如图,两个正方形的边长都为6,其中正方形 绕着正方形 的对角线的交点 旋转,正方形 与边 、 分别交于点 、 (不与端点重合),设两个正方形重叠部分形成图形的面积为 , 的周长为 ,则下列说法正确的是( )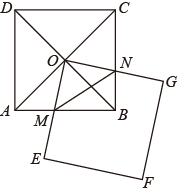 A、 发生变化, 存在最大值 B、 发生变化, 存在最小值 C、 不发生变化, 存在最大值 D、 不发生变化, 存在最小值
A、 发生变化, 存在最大值 B、 发生变化, 存在最小值 C、 不发生变化, 存在最大值 D、 不发生变化, 存在最小值二、填空题
-
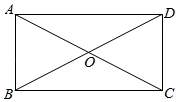
11. 若双曲线的图象经过第一、三象限,则k的取值范围是12. 如图,在矩形ABCD中,AB=4,对角线AC,BD相交于点O,∠AOB=60°,则对角线AC的长为.
 13. 如图,在平行四边形 ABCD中,AD=7,AB=5,DE平分∠ADC交BC于点E,则BE的长是 .
13. 如图,在平行四边形 ABCD中,AD=7,AB=5,DE平分∠ADC交BC于点E,则BE的长是 . 14. 如图,函数和函数的图象相交于点 , , 若 , 则x的取值范围是.
14. 如图,函数和函数的图象相交于点 , , 若 , 则x的取值范围是. 15. 对于任意实数a、b,定义一种运算: ,若 ,则x的值为.16. 如图,点A是反比例函数 的图象上一点,过点A作 轴于点C, 交反比例函数 的图象于点B,点P是y轴正半轴上一点.若 的面积为2,则k的值为.
15. 对于任意实数a、b,定义一种运算: ,若 ,则x的值为.16. 如图,点A是反比例函数 的图象上一点,过点A作 轴于点C, 交反比例函数 的图象于点B,点P是y轴正半轴上一点.若 的面积为2,则k的值为.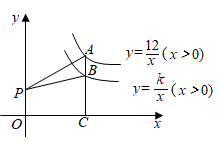 17. 若等腰三角形的一边长是4,另两边的长是关于 的方程 的两个根,则 的值为 .18. 如图,已知点A在反比例函数y=(x<0)上,B,C两点在x轴上,△ABC是以AC为底边的等腰直角三角形,过点B作BD⊥AC交y轴于点E,交AC于点D,若△BCE的面积为3,则k的值为 .
17. 若等腰三角形的一边长是4,另两边的长是关于 的方程 的两个根,则 的值为 .18. 如图,已知点A在反比例函数y=(x<0)上,B,C两点在x轴上,△ABC是以AC为底边的等腰直角三角形,过点B作BD⊥AC交y轴于点E,交AC于点D,若△BCE的面积为3,则k的值为 .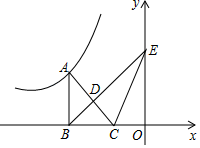
三、解答题
-
19. 解方程:(1)、x2-2x-3=0(2)、2x2+1=3x20. 如图,在平面直角坐标系xOy中,点A(2,0),B(5,0),C(4,2).
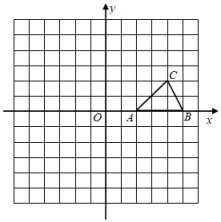 (1)、画出△ABC关于点O的中心对称图形,点A、B、C的对应点分别是D、E、F;(2)、若y轴上存在一点M,使得△MDF的周长最小,求点M的坐标.21. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.22. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)、画出△ABC关于点O的中心对称图形,点A、B、C的对应点分别是D、E、F;(2)、若y轴上存在一点M,使得△MDF的周长最小,求点M的坐标.21. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.22. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE. (1)、求证:BD=EC;(2)、当∠DAB为多少度时,四边形BECD为菱形?并说明理由.23. 如图,反比例函数 上的图象与一次函数 的图象相交于 , 两点.
(1)、求证:BD=EC;(2)、当∠DAB为多少度时,四边形BECD为菱形?并说明理由.23. 如图,反比例函数 上的图象与一次函数 的图象相交于 , 两点.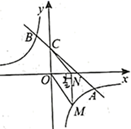 (1)、求反比例函数和一次函数的解析式;(2)、设直线 交y轴于点C,点 是正半轴上的一个动点,过点N作 轴交反比例函数 的图象于点M,连接 , .若 ,求t的取值范围.24. 某超市销售一种饮料,平均每天可售出100箱,每箱利润12元,为了扩大销售,增加利润,超市准备适当降价.据测算,每箱每降价1元,平均每天可多售出20箱.(1)、若每箱降价3元,每天销售该饮料可获利多少元?(2)、若要使每天销售该饮料获利1400元,则每箱应降价多少元?25. 方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.(1)、求v关于t的函数表达式;(2)、方方上午8点驾驶小汽车从A出发.
(1)、求反比例函数和一次函数的解析式;(2)、设直线 交y轴于点C,点 是正半轴上的一个动点,过点N作 轴交反比例函数 的图象于点M,连接 , .若 ,求t的取值范围.24. 某超市销售一种饮料,平均每天可售出100箱,每箱利润12元,为了扩大销售,增加利润,超市准备适当降价.据测算,每箱每降价1元,平均每天可多售出20箱.(1)、若每箱降价3元,每天销售该饮料可获利多少元?(2)、若要使每天销售该饮料获利1400元,则每箱应降价多少元?25. 方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.(1)、求v关于t的函数表达式;(2)、方方上午8点驾驶小汽车从A出发.①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
26. 在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.(1)、如图1,当点E恰好在AC上时,求∠CDE的度数;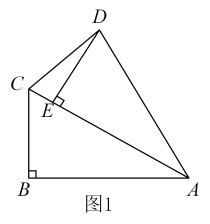 (2)、如图2,若=60° 时,点F是边AC中点,求证:四边形BFDE是平行四边形;
(2)、如图2,若=60° 时,点F是边AC中点,求证:四边形BFDE是平行四边形;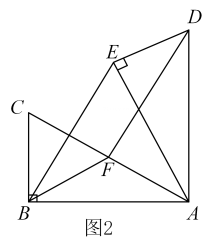 (3)、当BC=2时,连接CE,CD,设△CDE的面积为S.在旋转过程中,S是否存在最大值?若存在,请直接写出S的最大值;若不存在,请说明理由.27. 如图,已知四边形ABCD是平行四边形,AC为对角线,∠DAC=30°,∠ACD=90°,AD=8,点M为AC的中点,动点E从点C出发以每秒1个单位的速度运动到点B停止,连接EM并延长交AD于点F,设点E的运动时间为t秒.
(3)、当BC=2时,连接CE,CD,设△CDE的面积为S.在旋转过程中,S是否存在最大值?若存在,请直接写出S的最大值;若不存在,请说明理由.27. 如图,已知四边形ABCD是平行四边形,AC为对角线,∠DAC=30°,∠ACD=90°,AD=8,点M为AC的中点,动点E从点C出发以每秒1个单位的速度运动到点B停止,连接EM并延长交AD于点F,设点E的运动时间为t秒.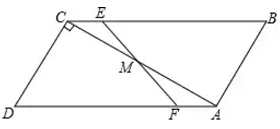 (1)、求四边形ABCD的面积;(2)、当∠EMC=90°时,判断四边形DCEF的形状,并说明理由;(3)、连接BM,点E在运动过程中是否能使△BEM为等腰三角形?如果能,求出t;如果不能,请说明理由.
(1)、求四边形ABCD的面积;(2)、当∠EMC=90°时,判断四边形DCEF的形状,并说明理由;(3)、连接BM,点E在运动过程中是否能使△BEM为等腰三角形?如果能,求出t;如果不能,请说明理由.