2022-2023学年冀教版数学九年级上册第二十三章数据分析 单元测试卷
试卷更新日期：2022-08-17 类型：单元试卷
一、单选题
-
1. 已知一组数据的方差s2＝[（6﹣7）2+（10﹣7）2+（a﹣7）2+（b﹣7）2+（8﹣7）2]（a，b为常数），则a+b的值为（ ）A、5 B、7 C、10 D、112. 某校九年级（3）班全体学生2021年中考体育模拟考试的成绩统计如表：
成绩（分）
36
40
43
46
48
50
54
人数（人）
2
5
6
7
8
7
5
根据上表中的信息判断，下列结论中错误的是（ ）
A、该班一共有40名同学 B、该班学生这次考试成绩的众数是48分 C、该班学生这次考试成绩的中位数是47分 D、该班学生这次考试成绩的平均数是46分3. 养鱼池养了同一品种的鱼，要大概了解养鱼池中的鱼的数量，池塘的主人想出了如下的办法：“他打捞出80尾鱼，做了标记后又放回了池塘，过了三天，他又捞了一网，发现捞起的90尾鱼中，带标记的有6尾．”你认为池塘主的做法（ ）A、有道理，池中大概有1200尾鱼 B、无道理 C、有道理，池中大概有7200尾鱼 D、有道理，池中大概有1280尾鱼二、填空题（每题4分，共24分）
-
4. 若数据a1、a2、a3的平均数是3，则数据2a1、2a2、2a3的平均数是.5. 某校中学生开展社会实践活动，同学们在某小区随机调查了部分家庭一周内使用环保方便袋的数量，整理后制作了如图所示的统计图，请你根据统计图估计该小区每户一周内使用环保方便袋 个.
6. 在对一组样本数据进行分析时，小华列出了方差的计算公式： ，由公式提供的信息，①样本的容量是4，②样本的中位数是3，③样本的众数是3，④样本的平均数是3.5，则说法错误的是（填序号）7. 某校倡导学生在家积极参加劳动，开学后，统计了部分学生在家每天劳动时间的情况，结果如下表：劳动时间（小时）
0.5
1
1.5
2
人数
10
12
6
2
则这些学生每天劳动时间的众数是小时．
8. 甲、乙两人的射击测试成绩统计如下：第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
8
8
9
乙命中环数
7
7
6
8
7
记甲测试成绩的方差为 ，乙测试成绩的方差为 ，则 填“ ”、“ = ”、“ ”中的一个 ．
9. 2021年6月17日，中国第7艘载人航天飞船“神舟十二号”圆满发射成功，激励更多的年轻人投身航天事业.现对学员们进行招飞前考核，其中某位学员心理素质、身体素质、科学头脑、应变能力四项测试得分分别为86分、85分、88分、90分，若按照心理素质、身体素质、科学头脑、应变能力的占比为4∶3∶2∶1的比例确定总分，则该名学员的总分为分.三、解答题（共8题，共66分）
-
10. 2022年2月4日，冬奥会开幕式在北京鸟巢拉开序幕，它让世界看到了一个自信开放的中国．某中学以此为契机，组织了“我的冬奥梦”系列活动．下表是小华和小敏各项目的成绩（单位：分）：如果将知识竞赛、演讲比赛、版面创作按5：3：2的比例确定最后成绩，请通过计算说明小华和小敏谁将获胜．
选手
知识竞赛
演讲比赛
版面创作
小华
85
91
88
小敏
90
84
87
11. 如图，是甲、乙两名射击运动员一次训练中10次射击环数折线统计图，请判断甲、乙两名射击运动员中谁的成绩的方差小，并计算其方差.
12. 海静中学开展以“我最喜爱的职业”为主题的调查活动，围绕“在演员、教师、医生、律师、公务员共五类职业中，你最喜爱哪一类？（必选且只选一类）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据图中提供的信息回答下列问题：
(1)、本次调查共抽取了多少名学生？(2)、求在被调查的学生中，最喜爱教师职业的人数，并补全条形统计图；(3)、若海静中学共有1500名学生，请你估计该中学最喜爱律师职业的学生有多少名？13. 某社区为了调查居民第三季度的用电情况，随机抽取了小区20户居民的用电量进行调查．数据如下：（单位：度）670，870，730，1140，700，690，1170，970，1000，970
730，840，1060，870，720，870，1060，930，840，870
整理数据：按如下分段整理样本数据并补至表格（表1）
用电量x（度）
人数
a
6
b
4
分析数据：补全下列表格中的统计量（表2）
平均数
中位数
众数
885
c
d
得出结论：
(1)、表中的a= ， b= ， c= ， d= ．(2)、若将表1中的数据制作成一个扇形统计图，则所表示的扇形圆心角的度数为度．(3)、如果该小区有住户400户，请根据样本估计用电量在的居民户数．14. 为深入开展青少年毒品预防教育工作，增强学生禁毒意识，某校联合禁毒办组织开展了“2021青少年禁毒知识竞赛”活动，并随机抽查了部分同学的成绩，整理并制作成图表如下：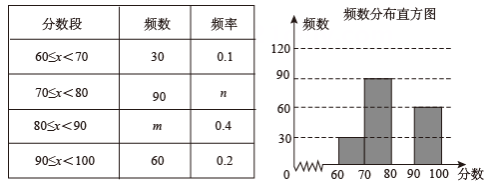
根据以上图表提供的信息，回答下列问题：
(1)、抽查的人数为人， ；(2)、请补全频数分布直方图；(3)、若成绩在80分以上（包括80分）为“优秀”，请你估计该校2400名学生中竞赛成绩是“优秀”的有多少名？15. 某篮球队对甲、乙两名运动员进行3分球投篮成绩测试，每天投3分球10次，五天中进球的个数统计结果如下：队员
第1天
第2天
第3天
第4天
第5天
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算，甲进球的平均数为8，方差为3.2．
(1)、求乙进球的平均数；(2)、现在需要根据以上结果，从甲、乙两名队员中选出一人去参加3分球投篮大赛，你认为应该选哪名队员参赛？为什么？16. 某校八年级举行了主题为“珍惜海洋资源”的知识竞赛活动，为了了解全年级500名学生此次参加竞赛的情况，随机抽取了部分参赛学生的成绩，整理并绘制出如下不完整的统计表和统计图．组别
分数（分）
频数
A
60≤x＜70
a
B
70≤x＜80
10
C
80≤x＜90
14
D
90≤x＜100
18
(1)、求a的值；(2)、所抽取的参赛学生成绩的中位数落在哪个组别？(3)、估计该校八年级竞赛成绩达到80分及以上的学生有多少人？17. 某校在八年级举行了一次数学文化知识竞赛，满分10分，学生得分均为整数，成绩超过5分为合格，超过8分为优秀．甲、乙两组学生（各10人）的成绩分布的折线统计图如图所示，成绩统计分布表如下表所示．
(1)、求出下列成绩统计表中、的值；组别
平均分
中位数
方差
合格率
优秀率
甲组
8
7.00
60%
40%
乙组
7.3
2.01
90%
30%
(2)、小李同学说：“这次竞赛我得了8分，在我们小组属于中游偏上！”通过观察，小李应该是哪一组的？(3)、乙组同学说他们组的合格率远高于甲组，所以他们组的成绩好于甲组，但甲组的同学不同意乙组同学的说法，认为他们组的成绩好于乙组．请你给出两条支持乙组同学观点的理由．