2022-2023学年冀教版数学九年级上册23.3方差 同步测试卷
试卷更新日期：2022-08-17 类型：同步测试
一、单选题
-
1. 我校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩（单位：m）如下：
甲
1.70
1.65
1.68
1.69
1.72
1.73
1.68
1.67
乙
1.60
1.73
1.72
1.61
1.62
1.71
1.70
1.75
借助计算器判断运动员的成绩更为稳定的是（ ）
A、甲 B、乙 C、一样稳定 D、无法判断2. 小明根据演讲比赛中9位评委所给的分数制作了如下表格：平均数
中位数
众数
方差
8.0
8.2
8.3
0.2
如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（ ）
A、平均数 B、中位数 C、众数 D、方差3. 为迎接建党一百周年，某班50名同学进行了党史知识竞赛，测试成绩统计如下表，其中有两个数据被遮盖.下列关于成绩的统计量中，与被遮盖的数据无关的是（ ）成绩/分
91
92
93
94
95
96
97
98
99
100
人数
■
■
1
2
3
5
6
8
10
12
A、平均数，方差 B、中位数，方差 C、中位数，众数 D、平均数，众数4. 已知一组数据的方差s2＝[（6﹣7）2+（10﹣7）2+（a﹣7）2+（b﹣7）2+（8﹣7）2]（a，b为常数），则a+b的值为（ ）A、5 B、7 C、10 D、115. 某选手在比赛中的成绩（单位：分）分别是90，87，92，88，93，方差是5.2（单位：分2），如果去掉一个最高分和一个最低分，那么该选手成绩的方差会（ ）A、变大 B、不变 C、变小 D、不确定6. 在第60届国际数学奥林匹克比赛中，中国队荣获团体总分第一名.我国参赛选手比赛成绩的方差计算公式为： ， 下列说法错误的是（ ）.A、我国一共派出了6名选手 B、我国参赛选手的平均成绩为38分 C、我国选手比赛成绩的中位数为38 D、我国选手比赛成绩的团体总分为228分7. 用计算器计算方差时，要首先进入统计计算状态，需要按键（ ）A、
B、
C、
D、
8. 用科学计算器求得271，315，263，289，300，277，286，293，297，280的平均数与方差（精确到0.1）分别为（ ）.A、287.1，14.4 B、287，14 C、287，14.4 D、14.4，287.19. 老师对甲、乙两位同学近六次数学测试成绩进行统计分析，已知甲的方差是2.2，甲的成绩比乙的成绩更稳定，则乙的方差可能是（ ）A、1.8 B、2 C、2.2 D、3.210. 2021 年，党中央国务院赋予浙江省建设“共同富裕示范区”的光荣使命，共同富裕的要求是： 在消除两极分化和贫穷基础上实现普遍富裕．下列有关人均收入的统计量特征中，最能体现共同富裕要求的是（ ）A、平均数大，方差大 B、平均数大，方差小 C、平均数小，方差小 D、平均数小，方差大二、填空题（每空2分，共10分）
-
11. 农科院助农团队在某地各选6块试验田试种甲、乙两种杂交水稻，收获后统计结果为：千克/亩， ， 千克/亩， ， 则品种更适合在该地区推广．（填“甲”或“乙”）12. 某校射击队从甲、乙、丙、丁四人中选拔一人参加射击比赛，在选拔赛中每人射击10次，计算他们10发成绩的平均数（环）及方差如下表.
甲
乙
丙
丁
平均数
8.2
8.0
8.2
8.0
方差
2.0
1.8
1.5
1.6
请你根据表中数据选择其中一人参加比赛，最合适的人选是.
13. 某班有50人，一次数学测试后，老师对测试成绩进行了统计．由于小明没有参加此次集体测试，因此计算其他49人的平均分为92分，方差 ．后来小明进行了补测，成绩是92分，则该班50人的数学测试成绩的方差 ．14. 现有5名同学的身高分别为165，172，168，170，175（单位：厘米）．增加1名身高为170的同学后，这6名同学身高的平均数和方差与原来相比，平均数（填“变大”、“变小”“不变”），方差（填“变大”、“变小”、“不变”）．三、综合题（共5题，共60分）
-
15. 甲、乙两人在相同的情况下各打靶6次，每次打靶的成绩依次如下（单位：环）：
甲：10，7，8，7，8，8
乙：5，6，10，8，9，10
(1)、甲成绩的众数 ， 乙成绩的中位数.(2)、计算乙成绩的平均数和方差；(3)、已知甲成绩的方差是1环，则的射击成绩离散程度较小.（填“甲”或“乙”）16. 某中学九年级学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀.下表是成绩最好的甲班和乙班5名学生的比赛成绩（单位：个）1号
2号
3号
4号
5号
总数
甲班
100
98
110
89
103
500
乙班
90
97
101
113
99
500
经统计发现两班5名学生踢毽子的总个数相等，此时有学生建议，可以通过考查数据中的其他信息为参考，请你回答下列问题：
(1)、甲班比赛数据的中位数为 ，乙班比赛数据的平均数为；(2)、计算两班比赛数据的方差；(3)、根据以上信息，你认为应该把冠军奖状发给哪一个班？简述理由.17. 某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出5名选手的决赛成绩如图所示.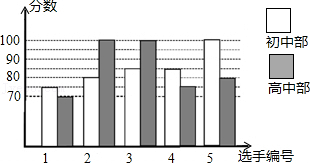
(1)、根据图示填表：平均数（分）
中位数（分）
众数（分）
初中部
85
高中部
85
100
(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.18. 甲、乙两位同学5次数学选拔赛的成绩统计如表，他们5次考试的总成绩相同，请同学们完成下列问题：第1次
第2次
第3次
第4次
第5次
甲成绩
80
40
70
50
60
乙成绩
70
50
70
a
70
(1)、统计表中，a＝ ， 甲同学成绩的极差为；(2)、小颖计算了甲同学的成绩平均数为60，方差是S甲2＝ [（80﹣60）2+（40﹣60）2+（70﹣60）2+（50﹣60）2+（60﹣60）2]＝200.请你求出乙同学成绩的平均数和方差；(3)、从平均数和方差的角度分析，甲、乙两位同学谁的成绩更稳定.19. 嘉淇同学利用业余时间进行射击训练，一共射击7次，经过统计，制成如图12所示的折线统计图．
(1)、这组成绩的众数是；(2)、求这组成绩的方差；(3)、若嘉淇再射击一次（成绩为整数环），得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数，求第8次的射击成绩的最大环数．