吉林省长春市农安县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{x + 1}{x - 2}$ 有意义，则x的取值应满足（）

A、 $x \neq 2$ B、 $x \neq - 1$ C、 $x = 2$ D、 $x = - 1$

查看试题解析
2. 化简 $\frac{x^{2}}{x - 1} + \frac{x}{1 - x}$ 的结果是（）

A、 $x$ +1 B、 $x - 1$ C、 $- x$ D、 $x$

查看试题解析
3. 生物学家发现了某种花粉的直径约为0.0000036毫米，数据0.0000036用科学记数法表示正确的是（）

A、3.6×10^﹣5 B、0.36×10^﹣5 C、3.6×10^﹣6 D、0.36×10^﹣6

查看试题解析
4. 下列函数中是正比例函数的是（）

A、y=-8x B、y= $\frac{- 8}{x}$ C、y=5x²+6 D、y= -0.5x-1

查看试题解析
5. 若点（3，1）在一次函数y=kx-2（k≠0）的图象上，则k的值是（）

A、5 B、4 C、3 D、1

查看试题解析
6. 若点A(3，－4)、B(－2，m)在同一个反比例函数的图象上，则m的值为（）

A、6 B、－6 C、12 D、－12

查看试题解析
7. 某校九年级“诗歌大会”比赛中，各班代表队得分如下（单位：分）：9，7，8，7，9，7，6，则各代表队得分的中位数是（）

A、9分 B、8分 C、7分 D、6分

查看试题解析
8. 如图在▱ABCD中，已知AC=4cm，若△ACD的周长为13cm，则▱ABCD的周长为（）

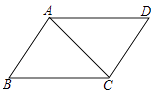A、26cm B、24cm C、20cm D、18cm

查看试题解析
9. 如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（）

A、 $\frac{1}{2}$ B、1 C、 $\sqrt{2}$ D、2

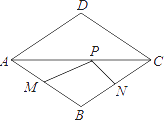查看试题解析
10. 如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE=32°，则∠GHC等于（）

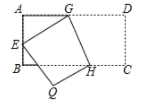A、112° B、110° C、108° D、106°

查看试题解析

二、填空题

11. 使分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，这时x= ．

查看试题解析
12. 化简： $(1 + \frac{1}{x - 1}) \cdot \frac{1}{x} =$ ．

查看试题解析
13. 方程 $\frac{1}{x} = \frac{4}{x + 6}$ 的解是

查看试题解析
14. 一组数3，4，7，4，3，4，5，6，5的众数是．

查看试题解析
15. 如果一次函数y=kx+3（k是常数，k≠0）的图象经过点（1，0），那么y的值随x的增大而．（填“增大”或“减小”）

查看试题解析
16. ▱ABCD的对角线AC与BD相交于点O，且AC⊥BD，请添加一个条件：，使得▱ABCD为正方形．

查看试题解析
17. 如图，四边形ABCD的对角线相交于点O，若AB//CD，请添加一个条件（写一个即可），使四边形ABCD是平行四边形．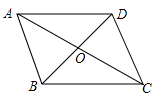

查看试题解析
18.
如图，点A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点C、D在x轴上，且BC∥AD，四边形ABCD的面积为3，则这个反比例函数的解析式为

查看试题解析
19. 如图，菱形 $A B C D$ 的面积为120cm² ，正方形 $A E C F$ 的面积为50cm²时，则菱形的边长为cm．

查看试题解析
20.
如图，点A在双曲线 $y = \frac{1}{x}$ 上，点B在双曲线y= $\frac{3}{x}$ 上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为 .

查看试题解析

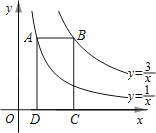
三、解答题

21. 先化简，再求值：（1﹣ $\frac{1}{a + 1}$ ）÷ $\frac{2 a}{a^{2} - 1}$ ，其中a=﹣3.

查看试题解析
22. 某同学参加了学校举行的“五好小公民•红旗飘飘”演讲比赛，7名评委给该同学的打分（单位：分）情况如下表：
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8

(1)、直接写出该同学所得分数的众数与中位数；

(2)、计算该同学所得分数的平均数

查看试题解析
23. 某校组织学生去9km外的郊区游玩，一部分学生骑自行车先走，半小时后，其他学生乘公共汽车出发，结果他们同时到达．已知公共汽车的速度是自行车速度的3倍，求自行车的速度和公共汽车的速度分别是多少？

查看试题解析
24. 如图，在四边形ABCD中，E是AB的中点，AD//EC，∠AED=∠B．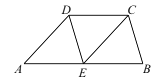

(1)、求证：△AED≌△EBC．

(2)、当AB=6时，求CD的长．

查看试题解析
25. 图①、图②、图③均是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1.

( 1 )在图①、图②中，以格点为顶点，线段AB为一边，分别画一个平行四边形和菱形，并直接写出它们的面积.(要求两个四边形不全等)

( 2 )在图③中，以点A为顶点，另外三个顶点也在格点上，画一个面积最大的正方形，并直接写出它的面积．

查看试题解析
26. 如图，在平面直角坐标系中， $▱$ OABC的顶点A， C的坐标分别为A(2，0)，C(-1，2)，反比例函数 $y= \frac{k}{x} (k \neq 0)$ 的图像经过点B．

(1)、求k的值．

(2)、将 $▱$ OABC沿着x轴翻折，点C落在点C′处．判断点C′是否在反比例函数 $y= \frac{k}{x} (k \neq 0)$ 的图像上，请通过计算说明理由．

查看试题解析
27. 某公司开发出一款新的节能产品，该产品的成本价为6元件，该产品在正式投放市场前通过代销点进行了为期30天的试销售，售价为8元/件，工作人员对销售情况进行了跟踪记录，并将记录情况绘成如图所示的图象，图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系，已知线段DE表示的函数关系中，时间每增加1天，日销售量减少5件.

(1)、第24天的日销售量是件，日销售利润是元.

(2)、求线段DE所对应的函数关系式.(不要求写出自变量的取值范围)

(3)、通过计算说明试销售期间第几天的日销售量最大？最大日销售量是多少？

查看试题解析
28. 如图①，正方形ABCD的边长为4．动点E从点A出发，以每秒2个单位的速度沿A→D→A运动；动点G从点A出发，以每秒1个单位的速度沿A→B运动，两点同时出发，当有一个点到达终点时，另一点随之也停止运动．过点G作FG⊥AB交AC于点F ．设运动时间为t（单位：秒）．以FG为一直角边向右作等腰直角三角形FGH ， △FGH与正方形ABCD重叠部分图形的面积为S ．

(1)、当t＝1.5时，S＝．

(2)、当t＝3时，求S的值．

(3)、设DE＝y ，在图②的坐标系中，画出y与t的函数图象．

(4)、当四边形DEGF是平行四边形时，求t的值．

查看试题解析

评委	评委1	评委2	评委3	评委4	评委5	评委6	评委7
打分	6	8	7	8	5	7	8