吉林省长春市南关区2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 若分式 的值为0,则x的值为A、3 B、 C、3或 D、02. 某种花的花粉颗粒直径约为0.0000065米,0.0000065这个数用科学记数法表示为()A、 B、 C、 D、3. 若点在第二象限,则m的取值范围是( )A、 B、 C、 D、4. 如图,的对角线、相交于点O,则下列结论一定成立的是()
 A、 B、 C、 D、5. 如图,在菱形中,对角线、相交于点O,于点E,若 , 则的大小为( )
A、 B、 C、 D、5. 如图,在菱形中,对角线、相交于点O,于点E,若 , 则的大小为( ) A、20° B、35° C、55° D、70°6. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、
A、20° B、35° C、55° D、70°6. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、 B、
B、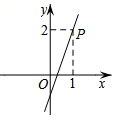 C、
C、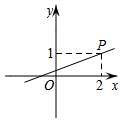 D、
D、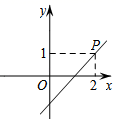 7. 如图,将正方形纸片折叠,使边、均落在对角线上,折痕为、 , 点E在上,点F在上,则的大小为( )
7. 如图,将正方形纸片折叠,使边、均落在对角线上,折痕为、 , 点E在上,点F在上,则的大小为( ) A、15° B、30° C、45° D、60°8. 如图,在平面直角坐标系中,函数的图象经过点P、Q、R,分别过这个三个点作x轴、y轴的平行线,阴影部分图形的面积从左到右依次为、、 , 若 , , 则k的值为( )
A、15° B、30° C、45° D、60°8. 如图,在平面直角坐标系中,函数的图象经过点P、Q、R,分别过这个三个点作x轴、y轴的平行线,阴影部分图形的面积从左到右依次为、、 , 若 , , 则k的值为( ) A、6 B、12 C、18 D、24
A、6 B、12 C、18 D、24二、填空题
-
9. 分式有意义的条件是 .10. 计算的结果为 .11. 已知函数 , 当函数值为0时,x的值为 .12. 某公司决定招聘广告策划人员一人,某应聘者三项素质测试的成绩(单位:分)如下:
测试项目
创新能力
综合知识
语言表达
测试成绩
90
80
75
如果将创新能力、综合能力和语言表达三项素质测试成绩按的比确定应聘者的最终成绩,则应聘者的最终成绩为分.
13. 如图,在菱形中,点E为边的中点,且 , 则的大小为度. 14. 如图,在正方形中,点E为边的中点,点P为对角线上一点,若 , 则的最小值为 .
14. 如图,在正方形中,点E为边的中点,点P为对角线上一点,若 , 则的最小值为 .
三、解答题
-
15. 计算: .16. 先化简,再求值: , 其中 .17. 某学校为了丰富学生的体育活动,购买了篮球和跳绳,已知每个篮球的价格是每个跳绳价格的3倍,购买跳绳共花费600元,购买篮球共花费900元,购买跳绳和数量比购买篮球的数量多20个,求每个跳绳的价格.18. 图①、图②均是的正方形网格,小正方形的边长为1,每个小正方形的顶点称为格点,点A、B均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,所画图形不全等,不要求写画法.
 (1)、在图①中以线段为边画一个正方形 .(2)、在图②中以线段为边画一个菱形 .19. 如图,在中, , 求其他各内角的大小.
(1)、在图①中以线段为边画一个正方形 .(2)、在图②中以线段为边画一个菱形 .19. 如图,在中, , 求其他各内角的大小. 20. 如图,为矩形的对角线,于点E,于点F.
20. 如图,为矩形的对角线,于点E,于点F. (1)、求证: .(2)、求证:四边形是平行四边形.21. 每年的4月15日是我国全民国家安全教育日,某中学在全校七、八年级学生中开展了“国家安全法”知识竞赛.为了解七、八年级学生对“国家安全法”知识的掌握情况,现从七、八年级各随机抽取20名学生的竞赛成绩(百分制),分数如下:
(1)、求证: .(2)、求证:四边形是平行四边形.21. 每年的4月15日是我国全民国家安全教育日,某中学在全校七、八年级学生中开展了“国家安全法”知识竞赛.为了解七、八年级学生对“国家安全法”知识的掌握情况,现从七、八年级各随机抽取20名学生的竞赛成绩(百分制),分数如下:七年级:82,58,73,80,75,74,85,64,75,95,75,79,82,68,75,80,92,85,84,79
八年级:92,72,90,81,72,81,93,82,78,83,80,81,71,81,72,77,82,80,70,41
对以上数据进行整理分析,得到下列表一和表二:
表一
七年级
0
a
2
b
7
2
八年级
1
0
0
7
9
3
表二
平均数
众数
中位数
七年级
78
n
八年级
78
m
80.5
根据以上信息,解答下列问题:
(1)、a的值为 , b的值为 , m的值为 , n的值为 .(2)、若该校七、八年级各有600人,估计该校七、八年级在本次竞赛成绩在90分以上的共有多少人.(3)、你认为哪个年级学生对“国家安全法”知识掌握的总体水平较好?请说明理由.22. 如图,在平面直角坐标系中,的顶点A、B在x轴的正半轴上,顶点D在y轴的正半轴上,函数的图象经过点C,点A、B、D的坐标分别为、、 . (1)、求k的值.(2)、将沿y轴向上平移,当点B落在函数的图象上时,求边与该函数图象的交点坐标.23. 如图,的对角线的垂直平分线与、分别交于E、F,垂足为点O.
(1)、求k的值.(2)、将沿y轴向上平移,当点B落在函数的图象上时,求边与该函数图象的交点坐标.23. 如图,的对角线的垂直平分线与、分别交于E、F,垂足为点O. (1)、求证:四边形是菱形.(2)、若 , , , 则的面积为 .24. 小亮家到公园的路程为2000米,小亮爸爸和小亮先后从家出发步行去公园,爸爸先出发一直匀速前行,小亮在爸爸走出200米时出发,途中他在休闲广场停留一段时间,小亮所走的路程y(米)与他步行的时间x之间的函数关系如图所示.
(1)、求证:四边形是菱形.(2)、若 , , , 则的面积为 .24. 小亮家到公园的路程为2000米,小亮爸爸和小亮先后从家出发步行去公园,爸爸先出发一直匀速前行,小亮在爸爸走出200米时出发,途中他在休闲广场停留一段时间,小亮所走的路程y(米)与他步行的时间x之间的函数关系如图所示. (1)、小亮步行的速度为米/分.(2)、在小亮出发后的第20分钟,爸爸行走了800米.
(1)、小亮步行的速度为米/分.(2)、在小亮出发后的第20分钟,爸爸行走了800米.①在平面直角坐标系中,画出爸爸所走的路程y(米)与小亮步行的时间x之间的函数图象并求其函数表达式.
②直接写出小亮出发多长时间爸爸与他相距300米.
25. 【教材呈现】如图时华师版八年级下册数学教材第104页的部分内容.如图,、是⊙O的两条直径,四边形是矩形吗?证明你的结论.


如图①,、是⊙O的两条直径.
(1)、【问题解决】求证:四边形是矩形.(2)、【发现结论】矩形的四个顶点都在以该矩形对角线的交点为圆心,对角线的长为直径的圆上.【结论应用】如图②,已知线段 , 以线段为对角线构成矩形 , 矩形面积的最大值为 .
(3)、【拓展延伸】如图③,在矩形中, , , 点E、F分别为边、的中点,以线段为对角线构造矩形 , 矩形的边与矩形的对角线交于M、N两点,当的长最长时,矩形的面积为 .