吉林省通化市梅河口市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 每年的6月5日为世界环境保护日,为提高学生环境保护意识,某校对100名学生进行“保护环境知多少”测试,抽取部分统计如下表:
成绩(分)
60
70
80
90
100
人数(人)
7
20
23
42
8
本次测验成绩的众数为( )
A、80分 B、85分 C、90分 D、100分3. 下列各组长度的线段能构成直角三角形的是直()A、 , , B、 , , C、 , , D、 , ,4. 如图在▱ABCD中,已知AC=4cm,若△ACD的周长为13cm,则▱ABCD的周长为( )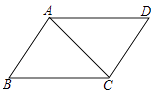 A、26cm B、24cm C、20cm D、18cm5. 已知菱形的边长和一条对角线的长均为2cm,则菱形的面积为( )A、3cm2 B、4cm2 C、 cm2 D、2 cm26. 已知将直线向上平移2个单位长度后得到直线 , 则下列关于直线的说法正确的是( )A、经过第一、二、四象限 B、与x轴交于 C、与y轴交于 D、y随x的增大而减小
A、26cm B、24cm C、20cm D、18cm5. 已知菱形的边长和一条对角线的长均为2cm,则菱形的面积为( )A、3cm2 B、4cm2 C、 cm2 D、2 cm26. 已知将直线向上平移2个单位长度后得到直线 , 则下列关于直线的说法正确的是( )A、经过第一、二、四象限 B、与x轴交于 C、与y轴交于 D、y随x的增大而减小二、填空题
-
7. 使得代数式 有意义的 的取值范围是 .
8. 已知 , , 则 .9. 如图,在中,对角线 , 相交于点O,点E是边的中点.若 , 则的长为 . 10. 学校广播站招聘记者时,综合成绩由3部分组成:采访写作占50%,电脑操作占20%,创意设计占30%.应聘者小明同学这3项成绩依次为90分、60分、70分,则小明同学的综合成绩为分.11. 如图,在 中, , , ,则 的长为.
10. 学校广播站招聘记者时,综合成绩由3部分组成:采访写作占50%,电脑操作占20%,创意设计占30%.应聘者小明同学这3项成绩依次为90分、60分、70分,则小明同学的综合成绩为分.11. 如图,在 中, , , ,则 的长为. 12. 已知A(﹣3,y1)、B(﹣2,y2)是一次函数y=﹣x﹣1图象上的两个点,则y1y2(填“>”、“<”或“=”).13. 若一次函数y=(2m﹣1)x+3﹣2m的图象经过 一、二、四象限,则m的取值范围是 .14. 如图,在矩形中, , , P是上一动点,且于E,于F,则的值为 .
12. 已知A(﹣3,y1)、B(﹣2,y2)是一次函数y=﹣x﹣1图象上的两个点,则y1y2(填“>”、“<”或“=”).13. 若一次函数y=(2m﹣1)x+3﹣2m的图象经过 一、二、四象限,则m的取值范围是 .14. 如图,在矩形中, , , P是上一动点,且于E,于F,则的值为 .
三、解答题
-
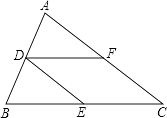
15. 计算: .16. 如图,在△ABC中,D、E、F分别为边AB、BC、CA的中点.
证明:四边形DECF是平行四边形.
 17. 如图所示是一块菜地,已知 , , , , , 求这块菜地的面积.
17. 如图所示是一块菜地,已知 , , , , , 求这块菜地的面积. 18. 已知正比例函数的图象经过点 .(1)、求这个正比例函数的解析式;(2)、直接写出点、点是否在这个函数的图象上.19. 如图,在中,点E,F分别在边 , 的延长线上,且 , 分别与 , 交于点G,H.求证 .
18. 已知正比例函数的图象经过点 .(1)、求这个正比例函数的解析式;(2)、直接写出点、点是否在这个函数的图象上.19. 如图,在中,点E,F分别在边 , 的延长线上,且 , 分别与 , 交于点G,H.求证 . 20. 如图,在正方形网格中,点A,B,C都在格点上,若小方格边长为1.
20. 如图,在正方形网格中,点A,B,C都在格点上,若小方格边长为1. (1)、试判断是什么形状,并说明理由;(2)、若D为边的中点,连接 , 求的长.21. 已知直线与x轴,y轴分别交于点 , .
(1)、试判断是什么形状,并说明理由;(2)、若D为边的中点,连接 , 求的长.21. 已知直线与x轴,y轴分别交于点 , . (1)、求直线的解析式;(2)、若第二、四象限的角平分线与直线交于点C,求的面积.22. 为进一步了解本班学生的小组学习情况,张老师将A、B两组学生成绩进行了统计.过程如下:
(1)、求直线的解析式;(2)、若第二、四象限的角平分线与直线交于点C,求的面积.22. 为进一步了解本班学生的小组学习情况,张老师将A、B两组学生成绩进行了统计.过程如下:【收集数据】
A组:
B组:
【整理数据】
整理以上数据,得到学生成绩x(分)的频数分布表:
成绩x/分
A组人数
B组人数
【分析数据】
根据以上数据,得到以下统计量:
统计量
平均数
中位数
方差
A组
b
B组
根据以上信息,回答下列问题:
(1)、表格中的a= , b=;(2)、求B组学生成绩的平均数;(3)、请你依据方差,分析两组学生学习成绩哪组比较稳定.23. 如图,正方形 中, 是 上的一点,连接 ,过 点作 ,垂足为点 ,延长 交 于点 ,连接 .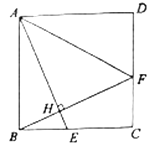 (1)、求证: .
(1)、求证: .
(2)、若正方形边长是5, ,求 的长.24. 如图,在矩形中,E是边上的点,沿折叠,点A的对应点为点G. (1)、如图1,当点G恰好在边上时,四边形的形状是;(2)、如图2,当是的中点,G在矩形内部时,延长交边于点F.
(1)、如图1,当点G恰好在边上时,四边形的形状是;(2)、如图2,当是的中点,G在矩形内部时,延长交边于点F.①求证:;
②若 , 试探索线段与的数量关系.
25. 如图,在中, , , , 点D从点C出发沿方向以秒的速度向点A匀速运动,同时点E从点A出发沿方向以秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒 . 过点D作于点F,连接 , . (1)、求证:;(2)、四边形能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)、直接写出当t为何值时,为直角三角形.26. 一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地.货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示.
(1)、求证:;(2)、四边形能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)、直接写出当t为何值时,为直角三角形.26. 一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地.货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示. (1)、甲乙两地相距多远?小轿车中途停留了多长时间?(2)、①写出y1与x的函数关系式;
(1)、甲乙两地相距多远?小轿车中途停留了多长时间?(2)、①写出y1与x的函数关系式;②当x≥5时,求y2与x的函数解析式;
(3)、货车出发多长时间与小轿车首次相遇?相遇时与甲地的距离是多少?