吉林省松原市前郭尔罗斯蒙古族自治县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 若式子 $\sqrt{2 - x} + \sqrt{x - 1}$ 有意义，则x的取值范围是（）

A、x≤2 B、x≥1 C、x≥2 D、1≤x≤2

查看试题解析
2. 已知 $A (- \frac{1}{3}$ ， $y_{1})$ 、 $B (- \frac{1}{2}$ ， $y_{2})$ 、 $C (1 ， y_{3})$ 是一次函数 $y = - 3 x + b$ 的图象上三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是 $($ $)$

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
3. 某次数学趣味竞赛共有10组题目，某班得分情况如下表．全班40名学生成绩的众数是（）

人数

$2$

$5$

$13$

$10$

$7$

$3$

成绩（分）

$50$

$60$

$70$

$80$

$90$

$100$

A、 $75$ B、 $70$ C、 $80$ D、 $90$

查看试题解析
4. 如图，数轴上的点 $A$ 表示的数是-1，点 $B$ 表示的数是1， $C B ⊥ A B$ 于点 $B$ ，且 $B C = 2$ ，以点 $A$ 为圆心， $A C$ 为半径画弧交数轴于点 $D$ ，则点 $D$ 表示的数为（）

A、 $2 \sqrt{2} - 1$ B、 $2 \sqrt{2}$ C、2.8 D、 $2 \sqrt{2} + 1$

查看试题解析
5. 如图，在Rt△ABC中，∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”，当AC＝4，BC＝2时，则阴影部分的面积为（　　）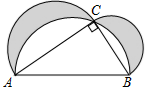

A、4 B、4π C、8π D、8

查看试题解析
6. 如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为（）

A、3 $\sqrt{2}$ B、2 $\sqrt{6}$ C、2 $\sqrt{5}$ D、2 $\sqrt{3}$

查看试题解析

二、填空题

7. 计算： $\sqrt{24} \times \sqrt{\frac{1}{6}} =$ ．

查看试题解析
8. 函数y= $\sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
9. 一次函数y=（2m﹣6）x+4中，y随x的增大而减小，则m的取值范围是．

查看试题解析
10. 将直线 $y = - \frac{1}{3} x - 1$ 向y轴正方向平移4个单位长度，得到的直线解析式是．

查看试题解析
11. 已知x+y= $\sqrt{3}$ ，xy= $\sqrt{6}$ ，则x²y+xy²的值为．

查看试题解析
12. 如图，一株荷叶高出水面 $1 m$ ，一阵风吹过，荷叶被风吹的贴着水面，这时它偏离原来位置有 $3 m$ 远，则荷叶原来的高度是 $m$ ．

查看试题解析
13. 某地出租车行驶里程 $x$ （ $k m$ ）与所需费用 $y$ （元）的关系如图.若某乘客一次乘坐出租车里程12 $k m$ ，则该乘客需支付车费元.

查看试题解析
14. 如图，在菱形ABCD中，AC、BD交于点O，BC=5，若DE∥AC，CE∥BD，则OE的长为．

查看试题解析

三、解答题

15. 计算： $\sqrt{8} \div \sqrt{2} - 4 \times \sqrt{\frac{1}{2}} \times {(\sqrt{2} - 1)}^{0}$

查看试题解析
16. 计算： ${(\sqrt{3} - \sqrt{2})}^{2} - (\sqrt{5} + 2) (\sqrt{5} - 2)$

查看试题解析
17. 已知 $a + 3$ 与 $2 a - 15$ 是一个正数的平方根，求这个正数．

查看试题解析
18. 已知y与x构成一次函数关系，当 $x = 0$ 时， $y = 3$ ，当 $x = 2$ 时， $y = 7$ ．

(1)、求y与x之间的一次函数关系式；

(2)、当 $x = 4$ 时的函数值．

查看试题解析
19. 图①、图②均是6×6的正方形网格，每个小正方形的边长为1，小正方形的顶点称为格点，点A、B均在格点上．用直尺在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写画法．

(1)、在图①中以线段AB为边画一个面积为12的平行四边形ABEF ．

(2)、在图②中以线段CD为对角线画一个面积为8的平行四边形CMDN ．

查看试题解析
20. 如图，一次函数 $y_{1} = x + 1$ 的图象与正比例函数 $y_{2} = k x$ （ $k$ 为常数，且 $k \neq 0$ ）的图象都过 $A (m ， 2)$

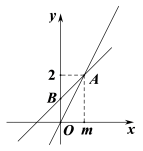(1)、求点A的坐标及正比例函数的表达式；

(2)、若一次函数 $y_{1} = x + 1$ 的图象与y轴交于点B，求 $Δ A B O$ 的面积；

(3)、利用函数图象直接写出当 $y_{1} > y_{2}$ 时，x的取值范围．

查看试题解析
21. 射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5

(1)、完成表中填空①；②；

(2)、请计算甲六次测试成绩的方差；

(3)、若乙六次测试成绩方差为 $\frac{4}{3}$ ，你认为推荐谁参加比赛更合适，请说明理由．

查看试题解析
22. 如图，已知矩形 $A B C D$ 中，E是 $A D$ 上的点，F是 $A B$ 上的一点， $E F ⊥ E C$ ，且 $E F = E C$ ， $D E = 4$ cm．

(1)、求证： $A F = D E$ ；

(2)、若 $A D + D C = 18$ cm，求 $A E$ 的长．

查看试题解析
23. 如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4 $\sqrt{2}$ 米．

(1)、求新传送带AC的长度．

(2)、如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点5米的货物MNQP是否需要挪走，并说明理由．
参考数据： $\sqrt{2} \approx 1.4 ， \sqrt{3} \approx 1.7$ ．

查看试题解析
24.

(1)、感知：如图①，在正方形 $A B C D$ 中，E是 $A B$ 一点，F是AD延长线上一点，且 $D F = B E$ ，求证： $C E = C F$ ；

(2)、拓展：在图①中，若G在AD，且 $∠ G C E = 45^{°}$ ，则 $G E = B E + G D$ 成立吗？为什么？

(3)、运用：如图②在四边形 $A B C D$ 中， $A D / / B C (B C > A D)$ ， $∠ A = ∠ B = 90^{°}$ ， $A B = B C = 16$ ， E是AB上一点，且 $∠ D C E = 45^{°}$ ， $B E = 4$ ，求DE的长．

查看试题解析
25. 为响应国家扶贫攻坚的号召，A市先后向B市捐赠两批货物，甲车以 $60 k m / h$ 的速度从A市匀速开往B市．甲车出发 $1 h$ 后，乙车以 $90 k m / h$ 的速度从A市沿同一条道路匀速开往B市．甲、乙两车距离A市的路程 $y (k m)$ 与甲车的行驶时间 $x (h)$ 之间的关系如图所示．

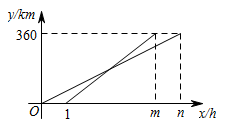(1)、A、B两市相距 $k m$ ， m= ， n=；

(2)、求乙车行驶的路程y与x之间的函数关系式，并写出自变量x的取值范围；

(3)、乙车出发后多少小时追上甲车：

(4)、在乙行驶的过程中，当甲、乙两车之间的距离为 $30 k m$ 时，求x的值．

查看试题解析
26. 如图，等腰△ABC中，已知AC＝BC＝ $\sqrt{10}$ ，AB＝2，作∠ACB的外角平分线CF，点E从点B沿着射线BA以每秒1个单位的速度运动，过点E作BC的平行线交CF于点F.

(1)、求证：四边形BCFE是平行四边形；

(2)、当点E是边AB的中点时，连接AF，试判断四边形AECF的形状，并说明理由；

(3)、设运动时间为t秒，是否存在t的值，使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形？不存在的，试说明理由；存在的，请直接写出t的值.

查看试题解析

人数	$2$	$5$	$13$	$10$	$7$	$3$
成绩（分）	$50$	$60$	$70$	$80$	$90$	$100$

	第一次	第二次	第三次	第四次	第五次	第六次	平均成绩	中位数
甲	10	8	9	8	10	9	9	①
乙	10	7	10	10	9	8	②	9.5