吉林省四平市铁西区2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 下列二次根式是最简二次根式的是()A、 B、 C、 D、2. 若3、4、a为勾股数,则a的值为( )A、-5 B、5 C、-5或 D、5或3. 在一次函数 中, 随 的增大而增大,那么 的值可以是( )A、1 B、0 C、 D、4. 如图,矩形ABCD中,对角线AC,BD交于点O,若∠AOB=60°,BD=8,则DC长为( )
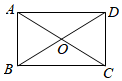 A、4 B、4 C、3 D、55. 在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差6. 在平面直角坐标系中,一次函数y=kx+b(k>0)的图象经过点(﹣1,0),则函数图象可能是( )A、
A、4 B、4 C、3 D、55. 在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差6. 在平面直角坐标系中,一次函数y=kx+b(k>0)的图象经过点(﹣1,0),则函数图象可能是( )A、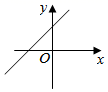 B、
B、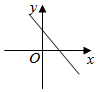 C、
C、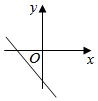 D、
D、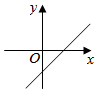
二、填空题
-
7. 若的值为零,则x的值为 .8. 已知一组数据:1,3,a,8,10的平均数是5,则a=.9. 若关于x的方程的解为 , 则直线一定经过某点的坐标为 .10. 若最简二次根式与能合并成一项,则a= .11. 已知平行四边形的一个内角平分线把一边分为 , 两部分,这个平行四边形的周长是 .12. 一次函数与的图象如图所示,则的解集为 .
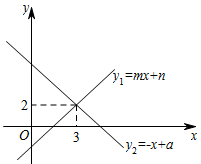 13. 如图,在长为8的线段上,作如下操作:经过点B作 , 使得;连接 , 在上截取;在上截取 , 则的长为 .
13. 如图,在长为8的线段上,作如下操作:经过点B作 , 使得;连接 , 在上截取;在上截取 , 则的长为 .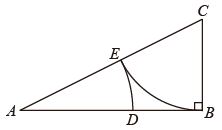 14. 图1是用一种彭罗斯瓷砖平铺成的图案,它的基础部分是“风筝”和“飞镖”两郎分,图2中的“风筝”和“飞镖”是由图3所示的特殊菱形制作而成.在菱形 中, ,在对角线 上截取 ,连按 , ,可将菱形分割为“风筝”(凸四边 )和“飞镖”(凹四边形 )两部分,则图2中的 °.
14. 图1是用一种彭罗斯瓷砖平铺成的图案,它的基础部分是“风筝”和“飞镖”两郎分,图2中的“风筝”和“飞镖”是由图3所示的特殊菱形制作而成.在菱形 中, ,在对角线 上截取 ,连按 , ,可将菱形分割为“风筝”(凸四边 )和“飞镖”(凹四边形 )两部分,则图2中的 °.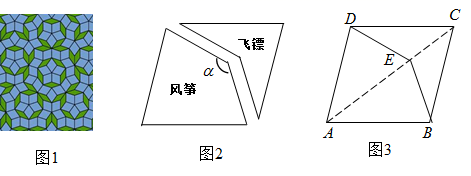
三、解答题
-
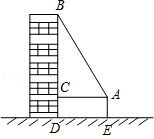
15. 计算:16. 计算: .17. 如图,一高层住宅发生火灾,消防车立即赶到距大厦8米处(车尾到大厦墙面),升起云梯到火灾窗口B.已知云梯长17米,云梯底部距地面的高米,问发生火灾的住户窗口距离地面多商?
 18. 图①、图②均为7×6的正方形网格,点A、B、C在格点上.
18. 图①、图②均为7×6的正方形网格,点A、B、C在格点上.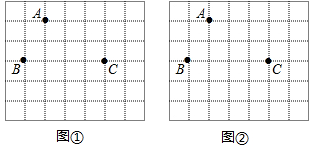 (1)、在图①中确定格点D,并画出以A、B、C、D为顶点的四边形,使其为轴对称图形.(画一个即可)(2)、在图②中确定格点E,并画出以A、B、C、E为顶点的四边形,使其为平行四边形.(画一个即可)19. 我校小李同学对北大附中初中三个年级的学生年龄构成很感兴趣,整理数据并绘制如图所示不完整的统计图.依据信息解答下列问题.
(1)、在图①中确定格点D,并画出以A、B、C、D为顶点的四边形,使其为轴对称图形.(画一个即可)(2)、在图②中确定格点E,并画出以A、B、C、E为顶点的四边形,使其为平行四边形.(画一个即可)19. 我校小李同学对北大附中初中三个年级的学生年龄构成很感兴趣,整理数据并绘制如图所示不完整的统计图.依据信息解答下列问题.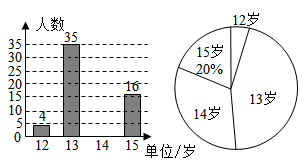 (1)、求样本容量;(2)、直接写出样本数据的众数、中位数;(3)、已知北大附中实验学校一共有1920名学生,请估计全校年龄在14岁及以上的学生大约有多少人.20. 在解决问题“已知 , 求的值”时,小明是这样分析与解答的:
(1)、求样本容量;(2)、直接写出样本数据的众数、中位数;(3)、已知北大附中实验学校一共有1920名学生,请估计全校年龄在14岁及以上的学生大约有多少人.20. 在解决问题“已知 , 求的值”时,小明是这样分析与解答的:,
,
请你根据小明的分析过程,解决如下问题:
若 , 求的值.
21. 在△ABC中,AB=AC,点D、E、F分别是AC、BC、BA延长线上的点,四边形ADEF为平行四边形.求证:AD=BF.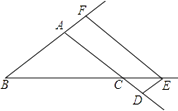 22. 如图,在平面直角坐标系中,直线y1=2x和直线y2=−x+m相交于点A . 且点A的纵坐标为2,点B在线段OA上(不与O、A重合),过点B作BC//x轴(自己完成)交直线y2=−x+m于点C .
22. 如图,在平面直角坐标系中,直线y1=2x和直线y2=−x+m相交于点A . 且点A的纵坐标为2,点B在线段OA上(不与O、A重合),过点B作BC//x轴(自己完成)交直线y2=−x+m于点C .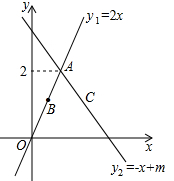 (1)、求m的值;(2)、若点B的横坐标为n , 则线段BC= . (用含n的代数式表示)23. 已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.
(1)、求m的值;(2)、若点B的横坐标为n , 则线段BC= . (用含n的代数式表示)23. 已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.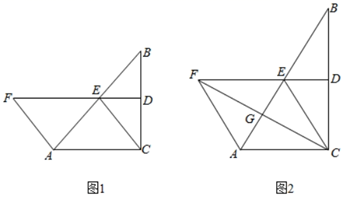 (1)、如图1,求证:四边形ACEF是平行四边形;(2)、如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的 倍.24. 从地面到高空,气温随离地面高度的变化而变化,当到达一定高度后,气温几乎不再变化.如图是气温 (℃)与离地面高度 ( )之间函数的图象.根据图象解答下列问题:
(1)、如图1,求证:四边形ACEF是平行四边形;(2)、如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的 倍.24. 从地面到高空,气温随离地面高度的变化而变化,当到达一定高度后,气温几乎不再变化.如图是气温 (℃)与离地面高度 ( )之间函数的图象.根据图象解答下列问题: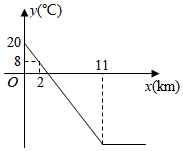 (1)、求地面的气温.(2)、当 时,求 与 之间的函数关系式.(3)、若离地面不同高度的两处气温差为3℃,直接写出这两处中较低处离地面高度 ( )的取值范围.25. 如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=3,AD=BC=7.延长BC到E , 使CE=4,连接DE , 由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC−CD−DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)、求地面的气温.(2)、当 时,求 与 之间的函数关系式.(3)、若离地面不同高度的两处气温差为3℃,直接写出这两处中较低处离地面高度 ( )的取值范围.25. 如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=3,AD=BC=7.延长BC到E , 使CE=4,连接DE , 由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC−CD−DA向终点A运动,设点P运动的时间为t秒.(t>0)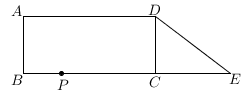
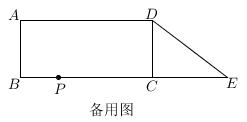 (1)、当时,;(用含t的代数式表示)(2)、请用含t的代数式表示的面积S;(不包括点P与点A重合的情况)(3)、当点P在BC边上时,直接写出点P到四边形ABED任意相邻两边距离相等时t的值.26. 如图1,在矩形ABCD中,AB=a , BC=6,动点P从B出发沿射线BC方向移动,作△PAB关于直线PA的对称△PAB′.
(1)、当时,;(用含t的代数式表示)(2)、请用含t的代数式表示的面积S;(不包括点P与点A重合的情况)(3)、当点P在BC边上时,直接写出点P到四边形ABED任意相邻两边距离相等时t的值.26. 如图1,在矩形ABCD中,AB=a , BC=6,动点P从B出发沿射线BC方向移动,作△PAB关于直线PA的对称△PAB′. (1)、如图2,当点P在线段BC上运动时,直线PB′与CD相交于点M , 连接AM , 若∠PAM=45°,请直接写出∠B′AM和∠DAM的数量关系;(2)、在(1)的条件下,请求出此时a的值:(3)、当a=8时,
(1)、如图2,当点P在线段BC上运动时,直线PB′与CD相交于点M , 连接AM , 若∠PAM=45°,请直接写出∠B′AM和∠DAM的数量关系;(2)、在(1)的条件下,请求出此时a的值:(3)、当a=8时,①如图3,当点B′落在AC上时,请求出此时PB的长;
②当点P在BC的延长线上时,请直接写出△PCB′是直角三角形时PB的长度.