吉林省四平市双辽市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{9}$

查看试题解析
2. 下列命题中，真命题是（　　）

A、有两边相等的平行四边形是菱形 B、有一个角是直角的四边形是矩形 C、四个角相等的菱形是正方形 D、两条对角线互相垂直且相等的四边形是正方形

查看试题解析
3. 小明家、食堂、图书馆在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家，如图反映了这个过程中，小明离家的距离y与时间x之间的对应关系．根据图象，下列说法正确的是（）

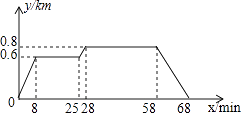A、小明吃早餐用了25min B、小明读报用了30min C、食堂到图书馆的距离为0.8km D、小明从图书馆回家的速度为0.8km/min

查看试题解析
4. 下列函数中，是正比例函数的是（）

A、y＝3x＋1 B、y＝x﹣1 C、y＝2x D、y＝x²

查看试题解析
5. 直线y＝kx＋b经过一、二、四象限，则k、b应满足（）

A、k＞0，b＜0 B、k＞0，b＞0 C、k＜0，b＜0 D、k＜0，b＞0

查看试题解析
6. 一组数据8，7，6，7，6，5，4，5，8，6的众数是（）

A、8 B、7 C、6 D、5

查看试题解析

二、填空题

7. 计算： $\sqrt{5} \times \sqrt{10} =$ ．

查看试题解析
8. 如图，在△ABC中，D、E分别是AB、BC的中点，点F在DE延长线上，添加一个条件使四边形ADFC为平行四边形，则这个条件是．

查看试题解析
9. 如图，一个正方形摆放在桌面上，则正方形的边长为．

查看试题解析
10. 从A地向B地打长途电话，按时收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若通话t分钟（t≥3），则需付电话费y（元）与t（分钟）之间的函数关系式是。

查看试题解析
11. 直线y＝2x+4沿x轴向右平移2个单位，再沿y轴向下平移3个单位所得直线解析式为

查看试题解析
12. 如图，三个正比例函数的图象分别对应的解析式是：①y＝ax ， ②y＝bx ， ③y＝cx ，请用“＞”表示a ， b ， c的不等关系是．

查看试题解析
13. 如图，一次函数 $y = k x + b$ 的图象与x轴的交点坐标为 $(- 2 ， 0)$ ，则下列说法：
$① y$ 随x的增大而减小； $② b < 0$ ； $③$ 关于x的方程 $k x + b = 0$ 的解为 $x = - 2$ ； $④$ 当 $x = - 1$ 时， $y < 0.$ 其中正确的是 $. ($ 请你将正确序号填在横线上 $)$

查看试题解析
14. 在学校团体操比赛中，甲、乙两个班的同学身高的平均数相同，方差分别是 $S_{甲}^{2} = 1.8$ ， $S_{乙}^{2} = 1.3$ ，那么身高整齐的是班．

查看试题解析

三、解答题

15. 计算：（ $\sqrt{3} + \sqrt{2}$ ）（ $\sqrt{3} - \sqrt{2}$ ）﹣（ $\sqrt{5} -$ 1）²

查看试题解析
16. 计算： $(\sqrt{12} - \sqrt{3}) \times \sqrt{6} - \sqrt{\frac{1}{2}}$

查看试题解析
17. 完成填空并在所给的直角坐标系中画出这个函数的图象（不必再列表）：一次函数y＝﹣x＋3过（0， ▲ ）和（ ▲ ， 0）．

查看试题解析
18. 如图，在正方形ABCD中，AE、DF相交于点O ，且AF＝BE ．求证：∠BAE＝∠ADF ．

查看试题解析
19. 如图，直线y＝kx＋b分别交x轴于点A（4，0）交y轴于点B（0，8）．

(1)、求直线AB的函数表达式：

(2)、若点P（2，m），点Q（n ， 2）是直线AB上两点，求线段PQ的长．

查看试题解析
20. 如图，在矩形ABCD中，过对角线AC的中点O作AC的垂线，分别交射线AD和CB于点E，F连接AF，CE.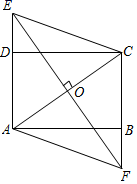

(1)、求证：OE＝OF；

(2)、求证：四边形AFCE是菱形.

查看试题解析
21. 直线y₁＝﹣x＋3和直线y₂＝kx﹣2分别交y轴于点A、B，两直线交于点C（2，m）.

(1)、求m，k的值；

(2)、求△ABC的面积；

(3)、根照图象直接写出当y₁＞y₂自变量x的取值范围.

查看试题解析
22. 在“慈善一日捐”活动中，为了解某校学生的捐款情况，抽样调查了该校部分学生的捐款数（单位：元），并绘制成如图所示的统计图．

(1)、本次调查的人数是；

(2)、这组数据的众数为元，中位数为元；

(3)、求这组数据的平均数．

查看试题解析
23. 如图（1），正方形ABCD的对角线AC ， BD相交于点O ， E是AC上一点，连接DE ，过点A作AM⊥DE ，垂足为M ， AM与BD相交于点F ．

(1)、直接写出OE与OF的数量关系：；

(2)、如图（2）若点E在AC的延长线上，AM⊥DE于点M ， AM交BD的延长线于点F ，其他条件不变．试探究OE与OF的数量关系，并说明理由．

查看试题解析
24. 如图，直线y＝kx＋4的图象与y轴交于点A ，与x轴交于点B（2，0），直线AF交x轴负半轴于点F ，且OF＝2OA ．

(1)、求出k的值为，直线AF的解析式为；

(2)、若将直线AB沿y轴向下平移，平移后的直线恰好经过C（﹣3，0），与y轴相交于点D ，且直线CD与直线AF交于点E ，求点E的坐标．

查看试题解析
25. 甲、乙两人从M地出发，甲先出发，乙后出发，都匀速骑车前往N地．乙在骑行途中休息片刻后，以原速度继续骑行．已知乙的速度是甲的1.6倍．甲、乙两人离M地的距离y（米）与乙行驶的时间x（分钟）之间的关系如图，请根据图象回答问题：

(1)、求甲骑行的速度；

(2)、求线段BD所表示的y与x之间的函数解析式；

(3)、求骑行途中甲、乙第二次相遇时x的值．

查看试题解析
26. 如图，四边形 $O A B C$ 是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正平轴上， $O A = 15 ， O C = 12$ .在 $O C$ 边上取一点D，将纸片沿 $A D$ 翻折，使点O落在 $B C$ 边上的点 $E$ 处.

(1)、求 $C E$ 和 $O D$ 的长；

(2)、求直线 $D E$ 的表达式；

(3)、直线 $y = k x + b$ 与 $A E$ 所在的直线垂直，当它与矩形 $O A B C$ 有公共点时，求出b的取值范围.

查看试题解析