吉林省吉林舒兰市2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 下列各式属于最简二次根式的是( )A、 B、 C、 D、2. 甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是8.9环,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,则射箭成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁3. 下列四组线段中,可以构成直角三角形的是( )A、2,3,4 B、4,5,6 C、1.5,2.5,3 D、1, ,4. 矩形具有而菱形不一定具有的性质是 ( )A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补5. 如图,直线 过点 和点 ,则方程 的解是( )
 A、 B、 C、 D、6. 如图,在平面直角坐标系中,点A的坐标为 , 沿x轴向右平移后得到 , 点A的对应点在直线上一点,则点B与其对应点间的距离为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,点A的坐标为 , 沿x轴向右平移后得到 , 点A的对应点在直线上一点,则点B与其对应点间的距离为( )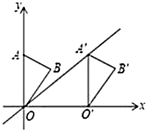 A、 B、3 C、4 D、5
A、 B、3 C、4 D、5二、填空题
-
7. 若式子 在实数范围内有意义,则x的取值范围是 .
8. 计算: = .9. 某灯泡厂为测试一批灯泡的使用寿命,从中随机抽查了50只灯泡,若抽出的50只灯泡的平均使用寿命为 , 则这批灯泡的平均使用寿命大约是 .10. 若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是.(写出一个即可)11. 自由落体的公式是(g为重力加速度,),若物体下落的高度h为 , 则下落的时间为s.12. 一木杆在离地面3米处折断,木杆顶端落在离木杆底端4米处,木杆折断之前高米.13. 如图,的周长为 , 中位线 , 中位线 , 则中位线的长为 .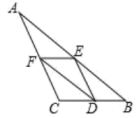 14. 如图,正方形的顶点A、C分别在坐标轴的正半轴上,点B是第一象限内直线上的一点,则点B的坐标为 .
14. 如图,正方形的顶点A、C分别在坐标轴的正半轴上,点B是第一象限内直线上的一点,则点B的坐标为 .
三、解答题
-
15. 计算: .16. 已知直角三角形中一条直角边长为4,如果斜边长与另一条直角边长的和是10,求斜边上的中线长.17. 若函数的图像平行于直线 , 求函数解析式.18. 某商场招聘员工一名,现有甲、乙两人竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示
应试者
计算机
语言
商品知识
甲
70
50
80
乙
90
75
45
若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2:3:5计算两名应试者的测试成绩,从他们的成绩看,应该录取谁?
19. 如图,平行四边形的对角线、相较于点O , 且 , , . 求证:四边形是矩形. 20. 在正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段的两个端点都在格点上.
20. 在正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段的两个端点都在格点上. (1)、在图1中,线段的长为;(2)、在图1中,画一个等腰直角三角形 , 且三角形的顶点都在格点上;(3)、在图2中,画一个面积为10的正方形 , 且正方形的顶点都在格点上.21. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:),绘制出如下的统计图1和图2,请根据相关信息,解答下列问题:
(1)、在图1中,线段的长为;(2)、在图1中,画一个等腰直角三角形 , 且三角形的顶点都在格点上;(3)、在图2中,画一个面积为10的正方形 , 且正方形的顶点都在格点上.21. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:),绘制出如下的统计图1和图2,请根据相关信息,解答下列问题: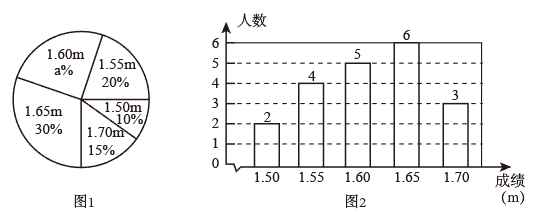 (1)、图1中成绩为的部分所占百分比为;参加跳高初赛的运动员有人.(2)、统计的这组初赛成绩的众数为m,中位数为m;(3)、根据这组初赛成绩,由高到低确定9人进入复赛,请问初赛成绩为的运动员能否进入复赛?(填“能”或“否”)22. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与正比例函数的图象交于点
(1)、图1中成绩为的部分所占百分比为;参加跳高初赛的运动员有人.(2)、统计的这组初赛成绩的众数为m,中位数为m;(3)、根据这组初赛成绩,由高到低确定9人进入复赛,请问初赛成绩为的运动员能否进入复赛?(填“能”或“否”)22. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与正比例函数的图象交于点 (1)、求一次函数的解析式;(2)、若直线与x轴交于点C,若连接后,请直接写出的面积是 .23. 某汽车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.邮箱中剩余油量Q(L)与行驶时间t(h)之间的函数关系如图所示.
(1)、求一次函数的解析式;(2)、若直线与x轴交于点C,若连接后,请直接写出的面积是 .23. 某汽车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.邮箱中剩余油量Q(L)与行驶时间t(h)之间的函数关系如图所示. (1)、汽车行驶h后加油,加油量为L;(2)、求加油前油箱剩余油量Q与行驶时间t之间的函数关系式;(3)、如果加油站离目的地还有200km,车速为40km/h,请直接写出汽车到达目的地时,油箱中还有多少汽油?24. 如图,四边形中, , E是边的中点,连接并延长与的延长线相交于点F.
(1)、汽车行驶h后加油,加油量为L;(2)、求加油前油箱剩余油量Q与行驶时间t之间的函数关系式;(3)、如果加油站离目的地还有200km,车速为40km/h,请直接写出汽车到达目的地时,油箱中还有多少汽油?24. 如图,四边形中, , E是边的中点,连接并延长与的延长线相交于点F. (1)、求证:四边形是平行四边形;(2)、若 , , . 直接写出四边形的周长 .25. 为响应国家扶贫攻坚的号召,A市先后向B市捐赠两批物资,甲车以的速度从A市匀速开往B市,甲车出发后,乙车以的速度从A市沿同一条道路匀速开往B市,甲、乙两车距离A市的路程与甲车的行驶时间之间的关系如图所示.
(1)、求证:四边形是平行四边形;(2)、若 , , . 直接写出四边形的周长 .25. 为响应国家扶贫攻坚的号召,A市先后向B市捐赠两批物资,甲车以的速度从A市匀速开往B市,甲车出发后,乙车以的速度从A市沿同一条道路匀速开往B市,甲、乙两车距离A市的路程与甲车的行驶时间之间的关系如图所示. (1)、两市相距 , m= , n=;(2)、求乙车行驶过程中y关于x的函数解析式,并写出x的取值范围;(3)、在乙车行驶过程中,当甲、乙两车之间的距离为时,直接写出x的值.26. 如图1,将边长为1的正方形压扁为边长为1的菱形 . 在菱形中,的大小为 , 面积记为S.
(1)、两市相距 , m= , n=;(2)、求乙车行驶过程中y关于x的函数解析式,并写出x的取值范围;(3)、在乙车行驶过程中,当甲、乙两车之间的距离为时,直接写出x的值.26. 如图1,将边长为1的正方形压扁为边长为1的菱形 . 在菱形中,的大小为 , 面积记为S. (1)、请补全下表:
(1)、请补全下表:30°
45°
60°
90°
120°
135°
150°
1
(2)、填空:由(1)可以发现边长是1的正方形在压扁的过程中,菱形的面积随着大小的变化而变化.不妨把边长为1,的菱形面积S记为 .例如:当时, , 当时,
由上表可以得到(°),(°),…,由此可以归纳出(°).
(3)、将两块相同的等腰直角三角形按图2的方式放置,若 , , 探究图中与的面积是否相等?并说明理由(友情提示:可以利用(2)的结论)