黑龙江省双鸭山市集贤县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt{3 a^{2}}$

查看试题解析
2. 下列各式中，计算正确的是（）

A、 $\sqrt{x} + \sqrt{y} = \sqrt{x + y}$ B、 $\sqrt{x} + \sqrt{y} = \sqrt{x y}$ C、 $\sqrt{16 a} \div 2 \sqrt{2} = \sqrt{2 a}$ D、 $\sqrt{x} \cdot \sqrt{x y} = x y$

查看试题解析
3. 由下列条件不能判定 $Δ A B C$ 为直角三角形的是（）

A、 $∠ A + ∠ B = ∠ C$ B、 $a ： b ： c = 1 ： 1 ： 2$ C、 $(b + c) (b - c) = a^{2}$ D、 $a = 1$ ， $b = \sqrt{2}$ ， $c = \sqrt{3}$

查看试题解析
4. 如图，四边形ABCD是菱形，对角线AC ， BD相交于点O ， DH⊥AB于点H ，连接OH ， ∠CAD＝20°，则∠DHO的度数是（　　）

A、20° B、25° C、30° D、40°

查看试题解析
5. 已知点 $P (- 1 ， y_{1})$ 、点 $Q (3 ， y_{2})$ 在一次函数 $y = (2 m - 1) x + 2$ 的图像上，且 $y_{1} > y_{2}$ ，则m的取值范围是（）

A、 $m < \frac{1}{2}$ B、 $m > \frac{1}{2}$ C、 $m \geq 1$ D、 $m < 1$

查看试题解析
6. 一次函数y＝－3x－2的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，一次函数 $y = - \frac{1}{2} x + 3$ 的图象分别与x轴、y轴交于点A、点B，与正比例函数的图象 $y = x$ 交于点C，则 $△ B O C$ 与 $△ A O C$ 的面积比为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{2}{3}$ D、2

查看试题解析
8. 为了帮助本市一名患“白血病”的高中生，某班15名同学积极捐款，他们捐款数额如下表：

捐款的数额（单位：元）

5

10

20

50

100

人数（单位：个）

2

4

5

3

1

关于这15名同学所捐款的数额，下列说法正确的是（）

A、众数是100 B、平均数是30 C、极差是20 D、中位数是20

查看试题解析
9. 某学校要招聘一名教师，分笔试和面试两次考试，笔试、面试和最后得分的满分均为100分，竞聘教师的最后得分按笔试成绩：面试成绩＝3∶2的比例计算．在这次招聘考试中，某竞聘教师的笔试成绩为90分，面试成绩为80分，则该竞聘教师的最后成绩是（）

A、43分 B、85分 C、86分 D、170分

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，点D，E为BC上两点. $∠ D A E = 45 °$ ， F为 $△ A B C$ 外一点，且 $F B ⊥ B C$ ， $F A ⊥ A E$ ，则下列结论：
① $C E = B F$ ；② $B D^{2} + C E^{2} = D E^{2}$ ；③ $S_{△ A D E} = \frac{1}{4} A D \cdot E F$ ；④ $C E^{2} + B E^{2} = 2 A E^{2}$ ，其中正确的是（）

A、①②③④ B、①②④ C、①③④ D、②③

查看试题解析

二、填空题

11. 要使代数式 $\frac{\sqrt{x + 3}}{2}$ 有意义，则x的取值范围是.

查看试题解析
12. 当x= $\sqrt{7} + 3$ 时，代数式x²-6x-2的值是.

查看试题解析
13.
如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件（只添一个即可），使四边形ABCD是平行四边形

查看试题解析
14. 一个样本为1，3，2，2，a，b，c.已知这个样本的众数为3，平均数为2，那么这个样本的方差为

查看试题解析
15. 直线y＝－x＋1向上平移5个单位后，得到的直线的解析式是．

查看试题解析
16. 在同一平面直角坐标系中，函数y₁＝kx+b与y₂＝mx+n的图象如图所示，则关于x的不等式kx+b≥mx+n的解集为．

查看试题解析
17. 矩形ABCD中，AB=5，BC=4，将矩形折叠，使得点B落在线段CD的点F处，则线段BE的长为.

查看试题解析
18. 在矩形 $A B C D$ 中， $A B = 4 ， A D = 8$ ，点P为线段 $A D$ 垂直平分线上一点，且 $P D = 5$ ，则 $B P$ 的长是．

查看试题解析
19. 如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE＝3，点Q为对角线AC上的动点，则QE＋QB的最小值为．

查看试题解析
20. 观察分析下列各式 $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}} ， \sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}} ， \sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}} ， \dots ，$ 按照上述三个等式及其变化过程，猜想第14个等式为

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{27} - \sqrt{8} \times \sqrt{\frac{2}{3}}$ ．

(2)、 $(3 \sqrt{2} + 1) (3 \sqrt{2} - 1)$ ．

查看试题解析
22. 如图，正方形网格中有△ABC．若每个小方格边长均为1，请你根据所学的知识解答下列问题：

(1)、判断△ABC的形状，并说明理由；

(2)、求△ABC中BC边上的高．

查看试题解析
23. 甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：
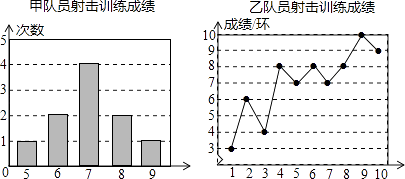
根据以上信息，整理分析数据如下：
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c

(1)、写出表格中a，b，c的值；

(2)、分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？

查看试题解析
24. 如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D ， E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F ，连接DE ， EF ．

(1)、求证：AE＝DF

(2)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，请说明理由；

(3)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析
25. 老陶手机店销售A型和B型两种型号的手机，销售一台A型手机可获利1200元，销售一台B型手机可获利1400元，手机店计划一次购进两种型号的手机共100台，其中B型手机的进货量不超过A型手机的3倍．设购进A型手机x台，这100台手机的销售总利润为y元．

(1)、求y与x的关系式；

(2)、该手机店购进A型、B型手机各多少台，才能使销售利润最大？

查看试题解析
26. 在四边形ABCD中，AB、BC、CD、DA的中点分别为P、Q、M、N ．

(1)、如图1，试判断四边形PQMN怎样的四边形，并证明你的结论；

(2)、若在AB上取一点E ，连结DE ， CE ，恰好△ADE和△BCE都是等边三角形（如图2），判断此时四边形PQMN的形状，并证明你的结论．

查看试题解析
27. 我市全民健身中心面向学生推出假期游泳优惠活动，活动方案如下．
方案一：购买一张学生卡，每次游泳费用按六折优惠；

方案二：不购买学生卡，每次游泳费用按八折优惠．

设某学生假期游泳x（次），按照方案一所需费用为 $y_{1}$ （元），且 $y_{1} = k_{1} x + b$ ；按照方案二所需费用为 $y_{2}$ （元），且 $y_{2} = k_{2} x$ ．其函数图象如图所示．

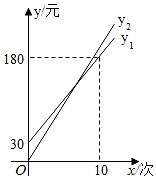(1)、求y₁关于x的函数关系式，并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用；

(2)、求打折前的每次游泳费用和k₂的值；

(3)、八年级学生小明计划假期前往全民健身中心游泳8次，应选择哪种方案所需费用更少？说明理由．

查看试题解析
28. 如图1，平面直角坐标系中，直线y=kx+b与x轴交于点A（6，0），与y轴交于点B ，与直线y=2x交于点C（a ， 4）．

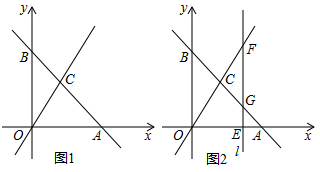(1)、求点C的坐标及直线AB的表达式；

(2)、如图2，在x轴上有一点E ，过点E作直线 $l$ ⊥x轴，交直线y=2x于点F ，交直线y=kx+b于点G ，若GF的长为3．求点E的坐标；

(3)、在y轴上是否存在一点F ，使以O、C、F为顶点的三角形是等腰三角形，若存在，直接写出点F的坐标；若不存在，说明理由．

查看试题解析

捐款的数额（单位：元）	5	10	20	50	100
人数（单位：个）	2	4	5	3	1

	平均成绩/环	中位数/环	众数/环	方差
甲	a	7	7	1.2
乙	7	b	8	c