黑龙江省齐齐哈尔市克山县2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、2. 若在实数范围内有意义,则x满足的条件是( )A、x≥ B、x≤ C、x= D、x≠3. 下列四个命题中,真命题是( )A、对角线互相垂直的四边形是菱形 B、对角线互相平分且垂直的四边形是矩形 C、顺次连接矩形四边中点得到的四边形是菱形 D、对角线互相垂直相等的四边形是正方形4. 下列线段的长不能构成直角三角形的是( )A、5,12,13 B、2,3, C、4,7,5 D、1, ,5. 一组数据﹣2,﹣1,x , 4,10的平均数为2,则这组数据的众数和中位数分别是( )A、﹣2,﹣2 B、﹣1,﹣1 C、﹣1,﹣2 D、﹣2,﹣16. 如图,过▱ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH , 那么图中的▱AEMG的面积S1与▱HCFM的面积S2的大小关系是( )
 A、S1=S2 B、S1>S2 C、S1<S2 D、不能确定7. 如图,平面直角坐标系中,在边长为 的正方形 的边上有一动点P沿A→D→C→B→A运动一周,则P的纵坐标y与P点走过的路程s之间的函数关系用图象表示大致是( )
A、S1=S2 B、S1>S2 C、S1<S2 D、不能确定7. 如图,平面直角坐标系中,在边长为 的正方形 的边上有一动点P沿A→D→C→B→A运动一周,则P的纵坐标y与P点走过的路程s之间的函数关系用图象表示大致是( ) A、
A、 B、
B、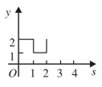 C、
C、 D、
D、 8. 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
8. 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )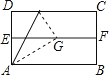 A、30° B、45° C、60° D、75°9. 在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( )A、14 B、42 C、32 D、42或3210. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角都是直角三角形.若A , B , C , D的边分别是5,3,3,2,则最大的正方形F的面积为( )
A、30° B、45° C、60° D、75°9. 在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( )A、14 B、42 C、32 D、42或3210. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角都是直角三角形.若A , B , C , D的边分别是5,3,3,2,则最大的正方形F的面积为( ) A、50 B、36 C、47 D、64
A、50 B、36 C、47 D、64二、填空题
-
11. 自去年以来新冠病毒肆虐全球,据世卫组织统计:全球累计新冠确诊病例超1亿7千万人,用科学记数法表示为 人.12. 要使代数式 有意义,则x的取值范围是 .
13. 写出同时具备下列两个条件:①y随x的增大而减小;②图象经过点(0,3)的一次函数表达式(写处一个即可)14. 矩形ABCD的对角线AC , BD交于点O , ∠AOB=60°,AB=4,矩形ABCD的面积为 .15. 在一次函数y=x+2的图象上,到x轴距离等于0.5的点的坐标是 .16. 如图,□ 中, 分别在边 上,要使 ,需要添加的条件是(只填一个你认为正确的即可). 17. 已知a= , b= , 则a2-2ab+b2的值为 .18. 已知点A(8,0)及第一象限内的动点P(x , y),且x+y=10,设△OPA的面积为S , 写出S关于x函数解析式 .19. 如图所示放置的 , ……,都是边长为2的等边三角形,边在x轴上,且点O、 , 都在同一直线上,则的坐标是 .
17. 已知a= , b= , 则a2-2ab+b2的值为 .18. 已知点A(8,0)及第一象限内的动点P(x , y),且x+y=10,设△OPA的面积为S , 写出S关于x函数解析式 .19. 如图所示放置的 , ……,都是边长为2的等边三角形,边在x轴上,且点O、 , 都在同一直线上,则的坐标是 .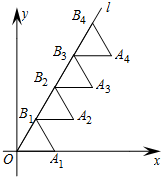
三、解答题
-
20. 计算:(1)、(+4)﹣(3﹣2);(2)、(+)2﹣(﹣)2;(3)、先化简,再求值:÷(),其中x=+1.21. 如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE、AF、EF.
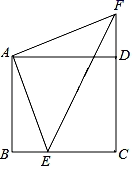 (1)、求证:△ABE≌△ADF;(2)、若AE=5,请求出EF的长.22. “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图:
(1)、求证:△ABE≌△ADF;(2)、若AE=5,请求出EF的长.22. “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图: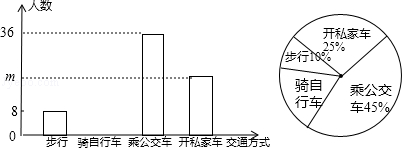 (1)、填空:样本中的总人数为;开私家车的人数m=;扇形统计图中“骑自行车”所在扇形的圆心角为度;(2)、补全条形统计图;(3)、该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?23. 在一条直线上的甲、乙两地相距240千米,快、慢两车同时出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地.在两车行驶的过程中,两车距甲地的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,请结合图象解答下列问题:
(1)、填空:样本中的总人数为;开私家车的人数m=;扇形统计图中“骑自行车”所在扇形的圆心角为度;(2)、补全条形统计图;(3)、该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?23. 在一条直线上的甲、乙两地相距240千米,快、慢两车同时出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地.在两车行驶的过程中,两车距甲地的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,请结合图象解答下列问题: (1)、求快、慢两车在行驶过程中的速度;(2)、求两车第二次相遇时,距甲地的距离是多少千米?(3)、求两车出发多长时间后,相距60千米?24. 已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)、求快、慢两车在行驶过程中的速度;(2)、求两车第二次相遇时,距甲地的距离是多少千米?(3)、求两车出发多长时间后,相距60千米?24. 已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.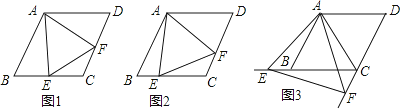 (1)、如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)、如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)、如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.25. 端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.(1)、请求出两种口味的粽子每盒的价格;(2)、设买大枣粽子x盒,买水果共用了w元.
(1)、如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)、如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)、如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.25. 端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.(1)、请求出两种口味的粽子每盒的价格;(2)、设买大枣粽子x盒,买水果共用了w元.①请求出w关于x的函数关系式;
②求出购买两种粽子的可能方案,并说明哪一种方案使购买水果的钱数最多.