黑龙江省齐齐哈尔富拉尔基区2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥ B、x> C、x≥ D、x>2. 在平行四边形ABCD中,若∠A∶∠B=5∶4,则∠C的度数为( )A、80° B、120° C、100° D、110°3. 矩形具有而菱形不具有的性质是( )A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等4. 若一组数据x , 3,1,6,3的中位数和平均数相等,则x的值为( )A、2 B、3 C、4 D、55. 下列命题的逆命题是真命题的是()A、若 , 则 B、四条边都相等的四边形是菱形 C、全等三角形的周长相等 D、无理数是无限小数6. 若点 , , 在一次函数的图像上,则 , , 的大小关系是( )A、 B、 C、 D、7. 一次函数的图象经过点P(-2,3),且与x轴、y轴分别交于点A、B , 则的面积是( )A、 B、 C、4 D、88. 如图,在中,点E为边DC上一点,连接AE , 将沿AE翻折,点D的对应点落在边AB上, , , 则边BC的长是( )
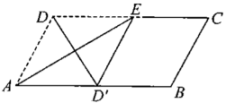 A、5 B、6 C、7 D、89. 如图,E , F是四边形ABCD两边AB , CD的中点,G , H是对角线AC , BD的中点,若EH=6,则以下结论错误的是( )
A、5 B、6 C、7 D、89. 如图,E , F是四边形ABCD两边AB , CD的中点,G , H是对角线AC , BD的中点,若EH=6,则以下结论错误的是( ) A、 B、 C、 D、10. 小明、小宇从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小宇骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:①小宇先到达青少年宫;②小宇的速度是小明速度的3倍;③a=20;④b=600.其中正确的是( )
A、 B、 C、 D、10. 小明、小宇从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小宇骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:①小宇先到达青少年宫;②小宇的速度是小明速度的3倍;③a=20;④b=600.其中正确的是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 已知 是正比例函数,且图像在第二、四象限内,则m的值是12. 如图,在四边形ABCD中,AC与BD相交于点O , 且 , , 请你添加一个条件,使四边形ABCD为矩形,你添加的条件是(填一个即可).
 13. 已知矩形ABCD的两边长分别为2和6,AE平分 , 交CD所在的直线于点E , 则BE的长为.14. 如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值是
13. 已知矩形ABCD的两边长分别为2和6,AE平分 , 交CD所在的直线于点E , 则BE的长为.14. 如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值是 15. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x > k1x+b的解集为
15. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x > k1x+b的解集为 16. 一组数据4,4,x , 8,8有唯一的众数,则这组数据的平均数是.17. 没有上盖的圆柱盒高为10cm,周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为cm.
16. 一组数据4,4,x , 8,8有唯一的众数,则这组数据的平均数是.17. 没有上盖的圆柱盒高为10cm,周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为cm.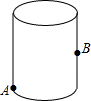 18. 如图,菱形 的边长为1, ;作 于点 ,以 为一边,做第二个菱形 ,使 ;作 于点 ,以 为一边做第三个菱形 ,使 ;……依此类推,这样做的第n个菱形 的边
18. 如图,菱形 的边长为1, ;作 于点 ,以 为一边,做第二个菱形 ,使 ;作 于点 ,以 为一边做第三个菱形 ,使 ;……依此类推,这样做的第n个菱形 的边的长是.

三、解答题
-
19.(1)、计算:(2)、若 , 试求的值.20. 如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.
 (1)、求∠CAE的度数;(2)、取AB边的中点F,连接CF、CE,试说明四边形AFCE是矩形.21. 为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
(1)、求∠CAE的度数;(2)、取AB边的中点F,连接CF、CE,试说明四边形AFCE是矩形.21. 为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
5.4
1
 (1)、请补全上述图表(请直接在表中填空和补全折线图);(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)、如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?22. 在一条公路上依次有A , B , C三地,甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地停留1小时后,按原路原速返回C地,两车匀速行驶,甲车比乙车晚1小时到达C地.两车距各自出发地的路程y(千米)与时间x(小时)之间的函数关系如图所示.请结合图象信息解答下列问题:
(1)、请补全上述图表(请直接在表中填空和补全折线图);(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)、如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?22. 在一条公路上依次有A , B , C三地,甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地停留1小时后,按原路原速返回C地,两车匀速行驶,甲车比乙车晚1小时到达C地.两车距各自出发地的路程y(千米)与时间x(小时)之间的函数关系如图所示.请结合图象信息解答下列问题: (1)、甲车行驶速度是千米/小时,A , B两地的路程为千米;(2)、求乙车从B地返回C地的过程中,y(千米)与x(小时)之间的函数关系式(不需要写出自变量x的取值范围);(3)、在乙车回到C地前,出发多少小时,两车之间的路程是15千米?请你直接写出答案.23. 综合与实践
(1)、甲车行驶速度是千米/小时,A , B两地的路程为千米;(2)、求乙车从B地返回C地的过程中,y(千米)与x(小时)之间的函数关系式(不需要写出自变量x的取值范围);(3)、在乙车回到C地前,出发多少小时,两车之间的路程是15千米?请你直接写出答案.23. 综合与实践折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图①:点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN , MN , AN , 如图②
 (1)、图②中,.线段F=.(2)、图②中,试判断的形状,并给出证明.
(1)、图②中,.线段F=.(2)、图②中,试判断的形状,并给出证明.剪一剪、折一折:将图②中的剪下来,将其沿直线GH折叠,使点A落在点处,分别得到图③、图④.
(3)、图③中,若 , 则°24. 综合与探究如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上, ,
 (1)、求点D的坐标.(2)、求直线BC的解析式.(3)、在x轴上是否存在点P , 使为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
(1)、求点D的坐标.(2)、求直线BC的解析式.(3)、在x轴上是否存在点P , 使为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.