黑龙江省牡丹江市2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 下列式子中,属于最简二次根式的是()A、 B、 C、 D、2. 下列运算正确的是()A、 B、 C、 D、3. 下列命题错误的是()A、一组对边平行,一组对角相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、有一条对角线平分一个内角的平行四边形是菱形 D、对角线互相垂直且相等的四边形是正方形4. 如图,在矩形 中, , ,动点 沿折线 从点 开始运动到点 .设运动的路程为 , 的面积为 ,那么 与 之间的函数关系的图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 某学习小组7位同学,为地震重灾区捐款,捐款金额分别为:4元,9元,5元,5元,6元,7元,8元,则这组数据的中位数与众数分别为( )A、 B、 C、 D、6. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、
5. 某学习小组7位同学,为地震重灾区捐款,捐款金额分别为:4元,9元,5元,5元,6元,7元,8元,则这组数据的中位数与众数分别为( )A、 B、 C、 D、6. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、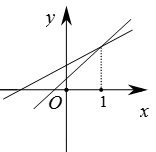 B、
B、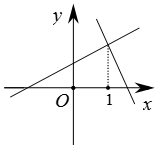 C、
C、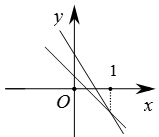 D、
D、 7. 如图,A,B,D三地在同直线上,C地在A地的北偏东方向.在B地的北偏西方向,A地在B地的北偏西方向,且km.则B地与C地之间的距离是( )
7. 如图,A,B,D三地在同直线上,C地在A地的北偏东方向.在B地的北偏西方向,A地在B地的北偏西方向,且km.则B地与C地之间的距离是( ) A、km B、km C、km D、km8. 已知平面直角坐标系中,点 , 点 , 直线经过点 , 且将的面积分成两部分,则k的值为( )A、 B、 C、或 D、 或9. 如图,中, , D是斜边上一点,把沿直线折叠,点A落在同一平面内的处,当时,线段的长为( )
A、km B、km C、km D、km8. 已知平面直角坐标系中,点 , 点 , 直线经过点 , 且将的面积分成两部分,则k的值为( )A、 B、 C、或 D、 或9. 如图,中, , D是斜边上一点,把沿直线折叠,点A落在同一平面内的处,当时,线段的长为( ) A、 B、 C、 D、10. 如图,四边形是正方形,线段交于点M,连接 , , 点E在线段上, , 于 . 下列结论:①;②;③平分;④;⑤若 , 则 , 其中正确结论的个数是( )
A、 B、 C、 D、10. 如图,四边形是正方形,线段交于点M,连接 , , 点E在线段上, , 于 . 下列结论:①;②;③平分;④;⑤若 , 则 , 其中正确结论的个数是( )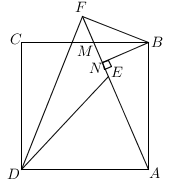 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数y= –1的自变量x的取值范围是.12. 如图,在平行四边形中, , 交于点O,请你添加一个条件 , 使 . (只填一种情况)
 13. 甲、乙两人在相同的条件下,各射靶10次,经过计算:甲射击成绩的方差是1.5,乙射击成绩的方差是1.4,射击成绩较稳定的是 .14. 将直线的图象向下平移3个单位后,经过点 , 则平移后的直线解析式为 .15. 若 , 则的值为 .16. 如图,直线与直线相交于点 , 则关于x的不等式的解集为 .
13. 甲、乙两人在相同的条件下,各射靶10次,经过计算:甲射击成绩的方差是1.5,乙射击成绩的方差是1.4,射击成绩较稳定的是 .14. 将直线的图象向下平移3个单位后,经过点 , 则平移后的直线解析式为 .15. 若 , 则的值为 .16. 如图,直线与直线相交于点 , 则关于x的不等式的解集为 . 17. △ABC中,AB=15,AC=13,高AD=12,则△ABC的面积为.18. 如图,中, , , , 是的角平分线,点E是的中点,P是上一点,则周长的最小值是 .
17. △ABC中,AB=15,AC=13,高AD=12,则△ABC的面积为.18. 如图,中, , , , 是的角平分线,点E是的中点,P是上一点,则周长的最小值是 . 19. 如图①,已知小正方形的面积为 , 把它的各边延长一倍得到新正方形;把正方形边长按原法延长一倍得到正方形(如图②)…以此下去,则正方形的面积为 .
19. 如图①,已知小正方形的面积为 , 把它的各边延长一倍得到新正方形;把正方形边长按原法延长一倍得到正方形(如图②)…以此下去,则正方形的面积为 . 20. 正方形的边长是6,p是正方形边上一点, , 则线段长为 .
20. 正方形的边长是6,p是正方形边上一点, , 则线段长为 .三、解答题
-
21. 计算:(1)、;(2)、;(3)、先化简,再求值: , 其中 .22. 如图,已知等腰 , , 平分 , E为上一动点,作平行 , 交于F,在上取一点G,使得 , 连接.
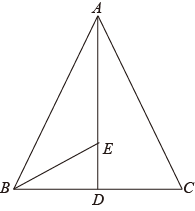 (1)、根据题意补全图形;(2)、求证四边形是平行四边形;(3)、若 , 写出一个的度数,使得四边形是菱形.23. 八年级一班的两位学生对本班的一次数学成绩(分数取整数,满分为分)进行了一次初步统计.看到分以上(含分)有人,但没有满分,也没有低于分的.为更清楚了解本班考试情况,他们分别用两种方式进行了统计分析,如图1和图2所示,请根据图中提供的信息解答下列问题:
(1)、根据题意补全图形;(2)、求证四边形是平行四边形;(3)、若 , 写出一个的度数,使得四边形是菱形.23. 八年级一班的两位学生对本班的一次数学成绩(分数取整数,满分为分)进行了一次初步统计.看到分以上(含分)有人,但没有满分,也没有低于分的.为更清楚了解本班考试情况,他们分别用两种方式进行了统计分析,如图1和图2所示,请根据图中提供的信息解答下列问题: (1)、班级共有名学生参加了考试,填上两个图中的空缺部分;(2)、参加考试的学生中分到分的学生有人;(3)、若全校八年级共有名学生,则八年级成绩在分的约有名学生.24. 某家电公司计划生产甲、乙两种空气净化器.已知生产一台甲种空气净化器比生产一台乙种空气净化器成本少万元;投入万元生产甲种空气净化器数量是投入万元生产乙种空气净化器数量的倍.请解答下列问题:(1)、该公司生产一台甲种空气净化器和生产一台乙种空气净化器成本各是多少万元?(2)、若该公司预计投人资金不低于万元生产这两种空气净化器共台,且甲种空气净化器至少生产台.设生产甲种空气净化器a台,该公司预计投人资金额y万元,求y与a的函数关系式,并求出公司这台空气净化器有哪几种生产方案;(3)、在(2)的条件下,已知生产台甲种空气净化器公司获利元,生产一台乙种空气净化器公司获利元.若该公司从生产这台空气净化器获利中拿出元用于设备维护,其余获利恰好又可以生产台空气净化器.请直接写出该公司这台空气净化器的生产方案.25. 是等边三角形,D是直线上的一点(点D不与点B,C重合),以为边作等边三角形 , 过点E作 , 交直线于点F,连接 . 请解答下列问题:
(1)、班级共有名学生参加了考试,填上两个图中的空缺部分;(2)、参加考试的学生中分到分的学生有人;(3)、若全校八年级共有名学生,则八年级成绩在分的约有名学生.24. 某家电公司计划生产甲、乙两种空气净化器.已知生产一台甲种空气净化器比生产一台乙种空气净化器成本少万元;投入万元生产甲种空气净化器数量是投入万元生产乙种空气净化器数量的倍.请解答下列问题:(1)、该公司生产一台甲种空气净化器和生产一台乙种空气净化器成本各是多少万元?(2)、若该公司预计投人资金不低于万元生产这两种空气净化器共台,且甲种空气净化器至少生产台.设生产甲种空气净化器a台,该公司预计投人资金额y万元,求y与a的函数关系式,并求出公司这台空气净化器有哪几种生产方案;(3)、在(2)的条件下,已知生产台甲种空气净化器公司获利元,生产一台乙种空气净化器公司获利元.若该公司从生产这台空气净化器获利中拿出元用于设备维护,其余获利恰好又可以生产台空气净化器.请直接写出该公司这台空气净化器的生产方案.25. 是等边三角形,D是直线上的一点(点D不与点B,C重合),以为边作等边三角形 , 过点E作 , 交直线于点F,连接 . 请解答下列问题: (1)、当点D在线段上时,如图①,求证:;(2)、当点D在线段延长线上时,如图②;当点D在线段延长线上时,如图③,请直接写出线段 , , 之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 , 则 .26. 甲、乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,途中因故停留1小时后按原速行驶到C地,到达C地后停止行驶;同时乙车从B地出发匀速向C地行驶,到达C地后,立即调头按原速向A地行驶(调头时间忽略不计),到达A地后停止行驶.在两车行驶的过程中,甲、乙两车距A地的路程y(千米)与所用时间x(小时)之间的函数图象如图所示,请结合图象解决下列问题:
(1)、当点D在线段上时,如图①,求证:;(2)、当点D在线段延长线上时,如图②;当点D在线段延长线上时,如图③,请直接写出线段 , , 之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 , 则 .26. 甲、乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,途中因故停留1小时后按原速行驶到C地,到达C地后停止行驶;同时乙车从B地出发匀速向C地行驶,到达C地后,立即调头按原速向A地行驶(调头时间忽略不计),到达A地后停止行驶.在两车行驶的过程中,甲、乙两车距A地的路程y(千米)与所用时间x(小时)之间的函数图象如图所示,请结合图象解决下列问题: (1)、A,B两地的路程是千米,甲车行驶的速度是千米/时,并直接在图中的()内填上正确的数;(2)、求图中线段表示的y与x的函数解析式(不用写自变量的取值范围);(3)、乙车行驶多长时间,行驶中的两车距B地的路程相等?直接写出答案.
(1)、A,B两地的路程是千米,甲车行驶的速度是千米/时,并直接在图中的()内填上正确的数;(2)、求图中线段表示的y与x的函数解析式(不用写自变量的取值范围);(3)、乙车行驶多长时间,行驶中的两车距B地的路程相等?直接写出答案.