江西省新余市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点(1,-2)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列问题中，不适合用全面调查的是（）

A、了解全省七年级学生的平均身高 B、旅客上飞机前的安检 C、学校招聘教师，对应聘人员面试 D、了解全班同学每周体育锻炼的时间

查看试题解析
3. 在实数3.14， $\frac{33}{7}$ ， $\sqrt{27}$ ， $- 5 π$ ， 0.3030030003……（每两个3之间依次多一个0）， $\sqrt{25}$ 中有理数有（）个

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 若 $a > b$ ，则下列不等式不一定成立的是（）

A、 $a - 5 > b - 5$ B、 $- 5 a < - 5 b$ C、 $a c^{2} > b c^{2}$ D、 $a + c > b + c$

查看试题解析
5. 如下图，在下列条件中，能判定AB//CD的是（）

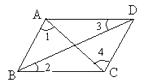A、∠1=∠3 B、∠2=∠3 C、∠1=∠4 D、∠3=∠4

查看试题解析
6. 如图，在平面直角坐标系中，半径均为1个单位长度的半圆组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒 $\frac{π}{2}$ 个单位长度，则第2022秒时，点P的坐标是（）

A、 $(2021 ， 0)$ B、 $(2022 ， - 1)$ C、 $(2021 ， - 1)$ D、 $(2022 ， 0)$

查看试题解析

二、填空题

7. $\sqrt{16}$ 的平方根是．

查看试题解析
8. 若关于x的不等式组 ${\begin{matrix} x - m < 0 \\ 7 - 2 x \leq 1 \end{matrix}$ 的整数解共有4个，则m的取值范围是．

查看试题解析
9. 把命题“同位角相等”改写成“如果……那么……”的形式为．

查看试题解析
10. 规定运算： $(a * b) = - | a - b |$ ，其中a、b为实数，则 $(\sqrt{10} * 4) - \sqrt{10} =$ ．

查看试题解析
11. 《九章算术》是中国古代数学专著，在数学上有其独到的成就，不仅最早提到了分数问题，也首先记录了“盈不足”等问题．如有一道阐述“盈不足”的问题，原文如下：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数、鸡价各几何？译文为：现有若干人合伙出钱买鸡，如果每人出9文钱，就会多11文钱；如果每人出6文钱，又会缺16文钱．设合作买鸡的有x人，鸡价为y文钱，则可列方程组为．

查看试题解析
12. 已知 $∠ A B C = 60 °$ ， $∠ D E F = 50 °$ ，若 $∠ D E F$ 的一边EF∥BC ，则另一边DE与直线AB相交于点P ，且点E不在直线AB上，则 $∠ A P D$ 的度数为．

查看试题解析
13. 已知 $2 a - 1$ 的算术平方根是5， $3 a + b - 1$ 的立方根是4，求 $a + 2 b + 35$ 的平方根．

查看试题解析

三、解答题

14.

(1)、计算： $\sqrt[3]{8} - 5 - | \sqrt{3} - 2 | + \sqrt{25}$ ；

(2)、解方程组： ${\begin{array}{l} 2 x + 3 y = - 20 \\ x + 5 y = 4 \end{array}$

查看试题解析
15. 解不等式组： ${\begin{array}{l} 3 (x - 1) < x \\ 1 - 2 x \leq \frac{x - 3}{2} \end{array}$ ，并在数轴上表示它的解集．

查看试题解析
16. 如图，直线AB、CD相交于点O ， OE平分 $∠ B O D$ ．

(1)、若 $∠ A O C = 70 °$ ， $∠ D O F = 90 °$ ，求 $∠ E O F$ 的度数；

(2)、若OF平分 $∠ C O E$ ， $∠ B O F = 18 °$ ，求 $∠ A O C$ 的度数．

查看试题解析
17. 在边长为1的小正方形网格中，△ABC的顶点均在格点上，

(1)、将△ABC向右平移4个单位长度，再向上平移2个单位长度得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ 并写出 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、求 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
18. 如图，已知 $∠ 1 = ∠ 2$ ， $∠ B = ∠ C$ ，可推得 $A B ∥ C D$ ．

理由如下：∵ $∠ 1 = ∠ 2$ （已知），且 $∠ 1 = ∠ C G D$ （        ），

∴ $∠ 2 = ∠ C G D$ （等量代换）．∴ $C E ∥ B F$ （       ）．

∴ $∠ B F D = ∠ C$        又∵ $∠ B = ∠ C$ （已知），

∴ $∠ B F D = ∠ B$ （       ），∴ $A B ∥ C D$ （       ）．

查看试题解析
19. 某校初一年级进行“垃圾分一分，环境美十分”的主题宣传活动，随机调查了部分学生对垃圾分类知识的了解情况．调查选项分为“A非常了解，B．比较了解，C．基本了解，D．不了解”四种，并将调查结果绘制成如图两幅不完整的统计图．
请根据图中提供的信息，解答下列问题：

(1)、本次调查的样本容量是；

(2)、把两幅统计图补充完整；

(3)、若该年级有1200名学生，请估计对垃圾分类非常了解的学生有多少人？

(4)、根据上述调查数据，请你提出一条合理化建议．

查看试题解析
20. 我们定义：若整式M与N满足 $M + N = k$ （k为整数）则称M与N为关于的平衡整式．例如，若 $2 x + 3 y = 4$ ，我们称 $2 x$ 与 $3 y$ 为关于4的平衡整式．

(1)、若 $2 a - 5$ 与 $4 a + 9$ 为关于1的平衡整式，求a的值；

(2)、若 $2 x - 9$ 与y为关于2的平衡整式， $3 x$ 与 $4 y + 1$ 为关于5的平衡整式，求 $x + y$ 的值．

查看试题解析
21. 在我市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元．

(1)、求每台电脑、每台电子白板各多少万元？

(2)、根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，该校有几种购买方案？

(3)、上面的哪种方案费用最低？按费用最低方案购买需要多少钱？

查看试题解析
22. 阅读下列材料解答问题：新定义：对非负数x“四舍五入”到个位的值记为 $〈 x 〉$ ，即：当n为非负整数时，如果 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ，则 $〈 x 〉 = n$ ；反之，当n为非负整数时，如果 $〈 x 〉 = n$ ，则 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ．例如： $〈 0.1 〉 = 〈 0.49 〉 = 0$ ， $〈 1.51 〉 = 〈 2.48 〉 = 2$ ， $〈 3 〉 = 3$ ， $〈 4.5 〉 = 〈 5.25 〉 = 5$ ， …，试解决下列问题：

(1)、① $〈 π + 3.4 〉 =$ （ $π$ 为圆周率）；②如果 $〈 x - 1 〉 = 2$ ，则数x的取值范围为；

(2)、求出满足 $〈 x 〉 = \frac{3}{4} x + 1$ 的x的取值．

查看试题解析
23. 如图，点A的坐标为 $(a ， 0)$ ，点B在y轴上，将△OAB沿x轴负方向平移，平移后的图形为△DEC ，且点C的坐标为 $(b ， 2)$ ，且a ， b满足 $\sqrt{a - 1} + | b + 3 | = 0$ ．

(1)、点E的坐标为，点B的坐标为；

(2)、在四边形ABCD中，点P从点B出发，沿“ $B C \to C D$ ”移动．若点P的速度为每秒1个单位长度，运动时间为t秒，回答下列问题：
①当 $t =$ 时，点P的横坐标与纵坐标互为相反数；

②当 $3 < t < 5$ 时，设 $∠ C B P = x °$ ， $∠ P A D = y °$ ， $∠ B P A = z °$ ，请问x ， y ， z之间的数量关系能否确定？若能，请用含x ， y的式子表示z ，若不能，请说明理由；

③当点P运动到什么位置时，直线OP将四边形ABCD的面积分成2：5两部分．

查看试题解析