江西省吉安市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列手机软件图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 $- (x - y) = - x + y$ C、 ${(2 x y^{2})}^{3} = 6 x^{3} y^{6}$ D、 ${(x + y)}^{2} = x^{2} + y^{2}$

查看试题解析
3. 下列诗词所描述的事件，不属于随机事件的是（）

A、黄梅时节家家田，青草池塘处处蛙 B、人间四月芳菲尽，山寺桃花始盛开 C、三月残花落更开，小檐日日燕飞来 D、水面上秤锤浮，直待黄河彻底枯

查看试题解析
4. 如图，点 $A$ 、 $D$ 在线段 $B C$ 的同侧，连接 $A B$ 、 $A C$ 、 $D B$ 、 $D C$ ，已知 $∠ A B C = ∠ D C B$ ，老师要求同学们补充一个条件使 $Δ A B C ≅ Δ D C B$ ．以下是四个同学补充的条件，其中错误的是 $($ 　　 $)$

A、 $A C = D B$ B、 $A B = D C$ C、 $∠ A = ∠ D$ D、 $∠ A B D = ∠ D C A$

查看试题解析
5. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式（）

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $a (a - b) = a^{2} - a b$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
6. 甲、乙两同学从同一地点同时出发去学校，甲骑自行车，乙步行，甲很快把乙甩在后头，不料自行车坏了，当甲修好自行车后，发现乙已经超过他，于是又奋力追赶，结果甲、乙同时到达学校． $S_{1}$ 、 $S_{2}$ 分别表示乙、甲走的路程，t为去学校的时间，则下列图象与上述情况大致相吻合的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

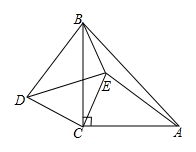
7. 新冠病毒的形状可近似看成球体其直径约为0.000000012米，用科学记数法表示为米．

查看试题解析
8. 已知一等腰三角形的两边长分别为1cm和3cm，则此三角形的周长为cm．

查看试题解析
9. 已知m＋n＝3，m－n＝2，则 $m^{2} - n^{2} =$ ．

查看试题解析
10. 如图，AC＝BC ， DC＝EC ， ∠ACB＝∠ECD＝90°，且∠EBD＝52°，则∠AEB＝．

查看试题解析
11. 如图“3×3”网格中，有3个涂成黑色的小方格，若再从余下的6个小方格中随机选取1个涂成黑色，则完成的图案为轴对称的概率是．

查看试题解析
12. 从点O引出三条射线OA ， OB ， OC ，已知∠AOB＝40°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，则∠AOC＝°．

查看试题解析

三、解答题

13.

(1)、化简： ${(- x^{2})}^{3} + (- x^{2}) x^{4}$

(2)、计算： $| - 3 | + {(- 1)}^{2022} \times {(π - 3)}^{0} - {(- \frac{1}{2})}^{- 3}$

查看试题解析
14. 如图AB ， CD相交于点O ， AO＝BO ， $A C ∥ D B$ ．那么OC与OD相等吗?

说明你的理由．小明的解题过程如下，请你说明每一步的理由．

解：OC＝OD ，理由如下：

∵ $A C ∥ D B$ （       ）

∴∠A＝∠B ， ∠C＝∠D（       ）

在△AOC和△BOD中

${\begin{array}{l} ∠ A = ∠ B (\underline{已证}) \\ ∠ C = ∠ D () \\ A O = B O () \end{array}$

∴ $△ A O C ≌ △ B O D$ （       ）

∴∠C＝∠D（       ）

查看试题解析
15. 先化简，再求值： $(2 a + 1) (2 a - 1) - 5 a (a - 1) + {(a - 1)}^{2}$ ，其中 $a = - \frac{1}{3}$

查看试题解析
16. 一口袋中有5张完全相同的卡片，分别写有1cm、2cm、3cm、4cm和5cm，口袋外有2张卡片，分别写有3cm和5cm．现随机从袋内取出一张卡片，与口袋外两张卡片放在一起，以卡片上的数量分别作为三条线段的长度．

(1)、求这三条线段能构成三角形的概率；

(2)、求这三条线段能构成等腰三角形的概率．

查看试题解析
17. 仅用无刻度的直尺画图，保留作图痕迹

(1)、在图（1）中的线段 $C D$ 上找一点P ，使点P到A、B两点的距离之和最短；

(2)、在图（2）中画出等腰梯形的对称轴 $M N$

查看试题解析
18. 如图，已知CD⊥DA，DA⊥AB， ∠1=∠2，试确定直线DF与AE的位置关系，并说明理由。

查看试题解析
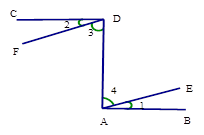19. 某课题小组为了了解某品牌电动自行车的销售情况，对某专卖店第一季度该品牌A，B，C，D四种型号的销售做了统计，绘制成如下两幅统计图（均不完整）

(1)、该店第一季度售出这种品牌的电动自行车共多少辆？

(2)、把两幅统计图补充完整；

(3)、若该专卖店计划订购这四款型号的电动自行车1800辆，求C型电动自行车应订购多少辆？

查看试题解析
20. 如图，是若干个粗细均匀的铁环最大限度的拉伸组成的链条，已知铁环粗0.6厘米，每个铁环长4厘米，设铁环间处于最大限度的拉伸状态．

(1)、2个、3个、4个铁环组成的链条长分别有多少?

(2)、设n个铁环长为y厘米，请用含n的式子表示y；

(3)、若要组成1.44米长的链条，需要多少个铁环?

查看试题解析
21. 如图1是一个大型的圆形花坛建筑物（其中 $A B$ 与 $C D$ 是一对互相垂直的直径）小川从圆心O出发，按图中箭头所小的方向匀速散步，并保持同样的速度走完下列三条线路：①线段 $O A$ ，②圆弧 $A \to C \to B \to D$ ，③线段 $D O$ 后，回到出发点．记小川所在的位置离出发点的距离为y（即所在位置与点O之间线段的长度）与时间t的关系如图2所示（注：圆周率π取近似值3）根据所给的信息，完成下列各题．

(1)、直接写出 $a =$ ， $b =$ ；

(2)、当 $t \leq 2$ 时，直接写出y与t的关系式；

(3)、在沿途某处小川遇见了他的好朋友小翔并在原地聊了两分钟的时间，然后继续保持原来的速度回到终点O ，请回答：
①小川与小翔的聊天地点位于何处？并求出此时他距离终点O还有多远？

②求他此行总共花了多少分钟的时间？

查看试题解析
22. 代数中的很多等式可以用几何图形直观表示，这种思想叫“数形结合”思想．如：现有正方形卡片A类、B类和长方形C类卡片若干张，如果要拼成一个长为 $2 (a + b)$ ，宽为 $(a + 2 b)$ 的大长方形，可以先计算 $(2 a + b) (a + 2 b) = 2 a^{2} + 5 a b + 2 b^{2}$ ，所以需要A、B、C类卡片2张、2张、5张，如图2所示

(1)、如果要拼成一个长为 $(a + 3 b)$ ，宽为 $(a + b)$ 的大长方形，那么需要A、B、C类卡片各多少张？并画出示意图．

(2)、由图3可得等式：；

(3)、利用（2）中所得结论，解决下面问题，已知 $a + b + c = 11$ ， $a b + b c + a c = 38$ ， $a^{2} + b^{2} + c^{2}$ 的值；

(4)、小明利用2张A类卡片、3张B类卡片和5张长方形C类卡片去拼成一个更大的长方形，那么该长方形的较长的一边长为（用含a、b的代数式表示）

查看试题解析
23. 在等腰 $R t △ A B C$ 中，AB＝AC ， $∠ B A C = 90 °$ ，以CA为边在∠ACB的另一侧作 $∠ A C M = ∠ A C B$ ，点D为射线BC上任意一点，在射线CM上截取CE＝BD ，连接AD、DE、AE ．

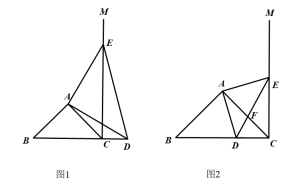(1)、如图1，当点D落在线段BC的延长线上时，试求∠ADE的度数；

(2)、如图2，当点D落在线段BC（不与B、C重合）上时，AC与DE交于点F ，请问（1）中的 $∠ A D E$ 的度数是否会改变?试说明理由．

查看试题解析