北京市燕山区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{5}$ 的相反数是（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $\pm \sqrt{5}$ D、 $\frac{1}{\sqrt{5}}$

查看试题解析
2. 北京2022年冬奥会的开幕式上，各个国家和地区代表团入场所持的引导牌是中国结和雪花融合的造型，如图1是中国体育代表团的引导牌．下面四个图案中，可以通过平移图1得到的是（）

图1

A、 B、 C、 D、

查看试题解析
3. 在数轴上表示不等式x－3≥0的解集，正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如图是天安门周围的景点分布示意图．在图中，分别以正东，正北方向为x轴，y轴的正方向建立平面直角坐标系．如果表示景山的点的坐标为(0，4)，表示王府井的点的坐标为(3，1)，则表示人民大会堂的点的坐标为（）

A、(3，2) B、(-1，2) C、(-1，-1) D、(-1，-2)

查看试题解析
5. 下列调查中，适合采用抽样调查方式的是（）

A、调查本校七年级(1)班学生每天完成数学作业所用的时间 B、调查全市中学生对电影《长津湖之水门桥》的喜爱程度 C、调查“神舟十四号”运载火箭发射前零部件质量状况 D、调查某封控区全体人员核酸检测情况

查看试题解析
6. 将一副三角尺(厚度不计)按如图所示摆放，使有刻度的两条边互相平行，则图中∠1的大小为（）

A、135° B、120° C、105° D、75°

查看试题解析
7. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子来量竿，却比竿子短一托．”其大意为，现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对折后再去量竿，就比竿短5尺．设绳索长x尺，竿长y尺，根据题意，可列方程组为（）

A、 ${\begin{array}{l} x - y = 5 \\ y - \frac{1}{2} x = 5 \end{array}$ B、 ${\begin{array}{l} y - x = 5 \\ y - \frac{1}{2} x = 5 \end{array}$ C、 ${\begin{array}{l} x - y = 5 \\ y - 2 x = 5 \end{array}$ D、 ${\begin{array}{l} y - x = 5 \\ y - 2 x = 5 \end{array}$

查看试题解析
8. 小周是一位运动达人，他通过佩戴智能手环来记录自己一个月(30天)的每日行走步数(单位：千步)，并绘制成右面的统计图．根据统计图提供的信息，下列推断不合理的是（）

A、每日行走步数为4～8千步的天数占这个月总天数的10% B、每日行走步数为8～12千步的扇形圆心角是108° C、小周这个月超过一半的天数每日行走步数不低于12000步 D、小周这个月行走的总步数不超过324千步

查看试题解析

二、填空题

9. 如图，利用量角器可知∠AOB的度数为．

查看试题解析
10. “x的一半与4的差是负数”用不等式表示：．

查看试题解析
11. 若 $a < b$ ，则 $- 2 a + 1$ $- 2 b + 1$ ．
(用“＞”，“＜”，或“＝”填空)

查看试题解析
12. 如图，要使CD $∥$ BE ，需要添加的一个条件为：．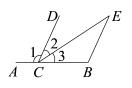

查看试题解析
13. 已知 ${\begin{array}{l} x = - 1 ， \\ y = 2 \end{array}$ 是方程为 $3 x + m y$ ＝5的解，则m的值为．

查看试题解析
14. 在平面直角坐标系中，点P(a ， 1)位于第二象限且到y轴的距离为2，则a的值是．

查看试题解析
15. 已知m是整数，且 $π$ <m< $\sqrt{37}$ ，请写出一个符合要求的m的值．

查看试题解析
16. 如图显示了某管控区12名社区工作者平均每天用于防疫宣传和排查登记的时间．(单位：小时)

(1)、小郑平均每天用于排查登记的时间是7小时，则他平均每天用于防疫宣传的时间为小时；

(2)、设平均每天用于排查登记的时间超过用于防疫宣传的时间的社区工作者为a人，则a的值为．

查看试题解析

三、解答题

17. 计算： $\sqrt{25} - \sqrt[3]{27} + | 2 - \sqrt{5} |$ ．

查看试题解析
18. 解不等式： $5 x + 1 > 3 x + 7$ ．

查看试题解析
19. 解方程组： ${\begin{array}{l} x + y = 4 \\ x - 2 y = 1 \end{array}$ .

查看试题解析
20. 解不等式组： ${\begin{array}{l} \frac{2 x - 8}{5} \leq x - 1 ， \\ 3 (2 + x) < 15 \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
21. 如图，点P为∠AOB内一点，根据下列语句画图并回答问题：

(1)、画图：①过点P画OB边的垂线，垂足为点M；②过点P画OB边的平行线，交OA于点N；

(2)、若∠O＝120°，则∠ANP＝°，依据是；

(3)、连接OP ，则线段OP与PM的大小关系是，依据是．

查看试题解析
22. 如图，已知AB∥CD ， CF为∠ACD的平分线，∠A＝110°，∠EFC＝35°．
求证：EF∥CD ．

请将下面的证明过程补充完整．

证明：∵AB∥CD ， (已知)

∴∠_▲_＋∠ACD＝180°．（）

∵∠A＝110°，（已知）

∴∠ACD＝_▲_°．(等量代换)

∵CF为∠ACD的平分线，(已知)

∴∠FCD＝ $\frac{1}{2}$ ∠_▲_＝35°．(角平分线定义)

∵∠EFC＝35°，(已知)

∴∠FCD＝∠EFC ， (等量代换)

∴EF∥CD ．（）

查看试题解析

23. 某中学为了解家长对课后延时服务的满意度，随机抽取50名学生家长进行问卷调查，获得了每位家长对课后延时服务的评分数据(记为x)，并对数据进行整理、描述和分析，制作了课后延时服务家长评分数据的频数分布表如下：

分组	划记	频数(人)	百分比
0≤x＜60		2	4%
60≤x＜70		5	10%
70≤x＜80		15	b
80≤x＜90		a	36%
90≤x≤100		10	20%

(1)、表中a＝， b＝．

(2)、下面是A ， B ， C三位同学分别绘制的课后延时服务家长评分数据的频数分布直方图，其中只有一位同学的作图符合题意，则作图正确的同学是；

(3)、已知该校共有600名学生家长参加了此次调查评分，请你估计其中大约有多少名家长的评分不低于80分．

查看试题解析

24. “冰墩墩”和“雪容融”作为第24届北京冬奥会和冬残奥会的吉祥物深受大家喜爱．某公司为奖励在趣味运动会上取得好成绩的员工，计划购买“冰墩墩”和“雪容融”玩偶共20件作为奖品．已知“冰墩墩”玩偶的零售单价是198元，“雪容融”玩偶的零售单价是100元．

(1)、如果购买“冰墩墩”和“雪容融”玩偶共花费了2784元，求“冰墩墩”和“雪容融”玩偶各购买了多少件？

(2)、如果购买“雪容融”玩偶的件数不超过“冰墩墩”玩偶件数的2倍，请为该公司设计一种最省钱的购买方案，并求出此时的总费用．

查看试题解析
25. 如图，点A ， B分别为∠MON的边OM ， ON上的定点，点C为射线ON上的动点(不与点O ， B重合)．连接AC ，过点C作CD⊥AC ，过点B作BE∥OA ，交直线CD于点F ．

图1 图2

(1)、如图1，若点C在线段OB的延长线上，
①依题意补全图1；

②用等式表示∠OAC与∠BFC的数量关系，并说明理由；

(2)、如图2，若点C在线段OB上，直接用等式表示出∠OAC与∠BFC的数量关系．

查看试题解析
26. 对于平面直角坐标系xOy中的任意一点P(x ， y)，给出如下定义：记a＝x $-$ y ， b＝x＋y ，将点M(a ， b)与点N(b ， a)称为点P的一对伴随点．例如，点M(5，1)与点N(1，5)为点P(3， $-$ 2)的一对伴随点．

(1)、点A(4，1)的一对伴随点坐标为；

(2)、将点C(m＋1，3m $-$ 1) (m＞0)向右平移m个单位长度，得到点 $C^{'}$ ，若点 $C^{'}$ 的一对伴随点重合，求点C的坐标；

(3)、已知点E(n ， $-$ 2)，F(n＋1， $-$ 2)，点D为线段EF上的动点，点G ， H为点D的一对伴随点．当点D在线段EF上运动时，线段GH与y轴总有公共点，请直接写出n的取值范围．

查看试题解析