北京市延庆区2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，直线AB ， CD相交于点O ，如果∠1=35°，那么∠2的度数是（）

A、 $35 °$ B、 $55 °$ C、 $145 °$ D、 $165 °$

查看试题解析
2. 2022年6月5日10时44分，搭载神舟十四号载人飞船的长征二号F遥十四运载火箭在酒泉卫星发射中心发射成功．中国对浩瀚星空的探索又迈入了一个全新的征程．北斗卫星导航系统提供定位和授时任务，其中授时精度为10纳秒，即： $0.00000001$ 秒．将 $0.00000001$ 用科学记数法表示为（）

A、 $1 \times 10^{8}$ B、 $1 \times 10^{9}$ C、 $1 \times 10^{- 8}$ D、 $1 \times 10^{- 9}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} \cdot a = a^{3}$ B、 ${(a + 2)}^{2} = a^{2} + 4$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(3 a^{2})}^{3} = 9 a^{6}$

查看试题解析
4. 下列调查方式，适合全面调查的是（）

A、调查北京市中学生每周体育锻炼时间 B、调查神舟十四号飞船零部件的质量 C、调查某一批次的计算器的使用寿命 D、调查全国中学生的视力情况

查看试题解析
5. 若 $a < b$ ，则下列不等式中，不成立的是（）

A、 $a - 2 < b - 2$ B、 $a + 3 < b + 3$ C、 $\frac{a}{3} < \frac{b}{3}$ D、 $- a < - b$

查看试题解析

6. 调查某超市的某种蔬菜一周内每天的销售量，结果统计如下表：

该种蔬菜一周内实际销售量表（单位：千克）
日期	周一	周二	周三	周四	周五	周六	周日
销售量	30	50	45	30	50	40	50

这一周中，该种蔬菜销售量的众数和中位数分别为（）

A、30，40 B、45，50 C、50，45 D、50，40

查看试题解析

7. 如图，点O在直线CD上，OB⊥OA ．若∠BOD＝110°，则∠AOC的度数为（）

A、10° B、20° C、60° D、70°

查看试题解析
8. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
9. 某同学要调查、分析本校七年级（1）班学生的身高状况，作为三年中跟踪调查的依据．
以下是排乱的统计步骤：

①绘制扇形统计图来表示各个身高范围所占的百分比；

②去校医务室收集学生入学后体检的有关数据；

③从扇形统计图中分析出学生身高状况；

④整理收集的相关数据，并按身高范围进行分组，在表格中表示出来．

正确统计步骤的顺序是（）

A、②→③→①→④ B、③→④→①→② C、①→②→④→③ D、②→④→①→③

查看试题解析
10. 如图，点E在BC的延长线上，下列条件中能判定CD $∥$ AB的是（）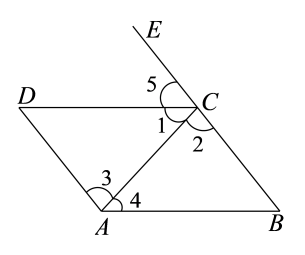

①∠1=∠4②∠2=∠3③∠5=∠B④∠DCB+∠B=180°

A、①②③④ B、①②③ C、①③④ D、①②

查看试题解析

二、填空题

11. 关于x的不等式的解集如图所示，则这个不等式的解集是．

查看试题解析
12. 分解因式： $3 x^{2} - 3 y^{2} =$ .

查看试题解析
13. 已知 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ 是关于x ， y的方程 $m x - 6 = 2 y$ 的一个解，那么m的值是．

查看试题解析
14. 用不等式表示“x的2倍与3的差大于4”：．

查看试题解析
15. 计算： ${(\frac{1}{2})}^{- 1} + {(π - 2)}^{0}$ ＝．

查看试题解析
16. 按规律排列的单项式： $- x$ ， $x^{3}$ ， $- x^{5}$ ， $x^{7}$ ， $- x^{9}$ ， … ，那么第15个单项式是．

查看试题解析
17. 已知：在同一平面内，三条直线a ， b ， c ．下列四个命题为真命题的是．（填写所有真命题的序号）
①如果a $∥$ b ， $a ⊥ c$ ，那么 $b ⊥ c$ ； ②如果 $b ⊥ a$ ， $c ⊥ a$ ，那么 $b ⊥ c$ ；

③如果a $∥$ b ， c $∥$ b ，那么a $∥$ c； ④如果 $b ⊥ a$ ， $c ⊥ a$ ，那么b $∥$ c ．

查看试题解析

18. 周末小明和妈妈外出共消费了300元，表中记录了他一天所有的消费项目以及部分支出．如果饼干每包13元，矿泉水每瓶2元，那么小明买了包饼干、瓶矿泉水．

项目

早餐

午餐

购买书籍

饼干

矿泉水

支出金额

（单位：元）

100

130

查看试题解析

三、解答题

19. 计算

(1)、 $15 x^{5} {(y^{4} z)}^{2} \div (- 3 x^{4} y^{5} z^{2})$ ．

(2)、 $(x + 1) (x - 1) + x (2 - x)$ ．

查看试题解析
20. 解不等式：2 （3x－1）≤x+3，并把它的解集在数轴上表示出来．

查看试题解析
21. 解不等式组： ${\begin{array}{l} x - 3 < 5 x + 1 ， \\ x - 2 < \frac{x - 1}{3} . \end{array}$ 并写出它的所有整数解．

查看试题解析
22. 解方程组：

(1)、 ${\begin{matrix} y = 2 x - 4 ， \\ x + y = 5. \end{matrix}$

(2)、 ${\begin{matrix} 2 x + 3 y = 7 ， \\ 3 x - 2 y = 4. \end{matrix}$

查看试题解析
23. 先化简，再求值： ${(a + b)}^{2} - b (2 a - b)$ ，其中 $a = - 3$ ， $b = 1$ ．

查看试题解析
24. 如图，∠B+∠BAD=180°，∠1=∠2．求证：AB $∥$ CD．请将下面的证明过程补充完整．

证明：

∵∠B+∠BAD=180°（已知），

∠1+∠BAD=180°（      ），

∴∠1=∠B（      ）．

∵∠1=∠2（已知），

∴∠2＝_▲_（      ）．

∴AB $∥$ CD（      ）．

查看试题解析

25. 某区图书馆充分发挥数字教育资源优势，利用“数字图书馆”组织开展了主题为“居家数字阅读+悦读”的中小学生寒假阅读主题活动．某校随机抽取了七年级的若干学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息回答下列问题．

七年级学生每天阅读时长情况统计表

组别	阅读时长（单位：小时）	人数（单位：人）
A	0＜x≤0.5	$a$
B	0.5＜x≤1	72
C	1＜x≤1.5	18
D	1.5＜x≤2	$b$

根据以上信息，回答下列问题：

(1)、求出表中a ， b的值；

(2)、已知该校七年级的学生有1000人，试估计该校七年级学生每天阅读时长在0.5＜x≤1.5的共有多少人？

查看试题解析

26. 某校七年级（1）班、（2）班的同学积极参加全民健身活动，为此两班到同一商店购买体育用品．已知七年级（1）班买了3个篮球和4副羽毛球拍共用了270元；七年级（2）班买了同样的5个篮球和6副羽毛球拍共用了430元；问每个篮球和每副羽毛球拍各多少元？

查看试题解析
27. 已知：如图，BD⊥AC于点D ，点E是线段BC上的任意一点（不与点B ， C重合），过点E作EF⊥AC于点F ，过点D作DG $∥$ BC交AB于点G ．

(1)、①请补全图形；
②求证：BD $∥$ EF；

(2)、用等式表示∠GDB与∠C的数量关系，并证明你的结论．

查看试题解析
28. 若不等式（组）只有n个正整数解（n为自然数），则称这个不等式（组）为n阶不等式（组）．
我们规定：当 $n = 0$ 时，这个不等式（组）为0阶不等式（组）．

例如：不等式 $x + 1 < 6$ 只有4个正整数解，因此称其为4阶不等式．

不等式组 ${\begin{array}{l} x + 1 > 2 ， \\ 2 x - 3 < 7. \end{array}$ 只有3个正整数解，因此称其为3阶不等式组．

请根据定义完成下列问题：

(1)、 $x < \frac{1}{2}$ 是阶不等式； ${\begin{array}{l} x > 1 ， \\ x - 3 < 0. \end{array}$ 是阶不等式组；

(2)、若关于x的不等式组 ${\begin{array}{l} x \geq 1 ， \\ x < a . \end{array}$ 是4阶不等式组，求a的取值范围；

(3)、关于x的不等式组 ${\begin{array}{l} x \geq p ， \\ x < m . \end{array}$ 的正整数解有 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， …，其中 $a_{1} < a_{2} < a_{3} < a_{4} <$ …．如果 ${\begin{array}{l} x \geq p ， \\ x < m . \end{array}$ 是 $(m - 3)$ 阶不等式组，且关于 $x$ 的方程 $2 x - m = 0$ 的解是 ${\begin{array}{l} x \geq p ， \\ x < m . \end{array}$ 的正整数解 $a_{3}$ ，直接写出 $m$ 的值以及 $p$ 的取值范围．

查看试题解析