北京市东城区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 在以下四个有关统计调查的说法中，正确的是（）

A、全面调查适用于所有的调查 B、为了解全体学生的视力，对每位学生进行视力检查，是全面调查 C、为调查小区1500户家庭用水情况，抽取该小区100户家庭，样本容量为1500 D、为了解全校中学生的身高，以该校篮球队队员的身高作为样本，能客观估计总体

查看试题解析
2. 如图，在数轴上表示的x的取值范围是（）

A、 $x < 2$ B、 $x \leq 2$ C、 $x > 2$ D、 $x \geq 2$

查看试题解析
3. 在数轴上，点A ， B，C表示的数分别为 $\sqrt{2}$ ， $\sqrt[3]{- 5}$ ， 0，则从左到右，点A ， B，C的排列顺序为（）

A、 $A B C$ B、 $B C A$ C、 $B A C$ D、 $C B A$

查看试题解析
4. 如图，纸片的边缘 $A B$ ， $C D$ 互相平行，将纸片沿 $E F$ 折叠，使得点B，D分别落在点 $B^{'}$ ， $D^{'}$ 处．若 $∠ 1 = 80 °$ ，则 $∠ 2$ 的度数是（）

A、 $50 °$ B、 $60 °$ C、 $70 °$ D、 $80 °$

查看试题解析
5. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是二元一次方程 $a x + 3 y = 0$ 的解，则点 $(a ， a - 3)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 中国象棋中的“马”沿“日”形对角线走，俗称马走日．三个棋子位置如图，若建立平面直角坐标系，使帅、相所在点的坐标分别为 $(- 1 ， - 1)$ ， $(1 ， 2)$ ，则马直接走到第一象限时所在点的坐标是（）

A、 $(0 ， 1)$ B、 $(3 ， 0)$ C、 $(2 ， 1)$ D、 $(1 ， 2)$

查看试题解析
7. 实数a，b，c在数轴上对应点的位置如图所示，在下列四个式子中，正确的是（）

A、 $| c | > | a |$ B、 $- c > a$ C、 $a c^{2} > b c^{2}$ D、 $a - c < b - c$

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，以O，A，B，C为顶点的正方形的边长为3．若点A在x轴上，点C在y轴的正半轴上，则点B的坐标为（）

A、 $(3 ， 3)$ B、 $(3 ， - 3)$ C、 $(3 ， 3)$ 或 $(- 3 ， 3)$ D、 $(- 3 ， - 3)$ 或 $(3 ， - 3)$

查看试题解析
9. 已知 $- 3 < x < 3$ ，下列四个结论中，正确的是（）

A、 $| x | > 3$ B、 $| x | < 3$ C、 $0 < | x | \leq 3$ D、 $0 < | x | < 3$

查看试题解析
10. 已知四个式子：① $2^{2} < 5 < 3^{2}$ ；② ${2.2}^{2} < 5 < {2.3}^{2}$ ；③ ${2.23}^{2} < 5 < {2.24}^{2}$ ；④ ${2.236}^{2} < 5 < {2.237}^{2}$ ．利用有理数逼近无理数的方法，估计 $\sqrt{5}$ 的近似值（精确到0.01）是（）

A、2.15 B、2.23 C、2.24 D、2.25

查看试题解析

二、填空题

11. 如图，在三角形 $A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ， $A B = 5$ ，则点A到 $B C$ 的距离等于.

查看试题解析
12. 如图，雷达探测器探测到三艘船A，B，C，按照目标表示方法的规定，船A，B的位置分别表示为 $A (5 ， 30 °)$ ， $B (6 ， 300 °)$ ，船C的位置应表示为.

查看试题解析
13. 若一个正数的平方根为 $x + 1$ 和 $5 + 2 x$ ，则x的值为，代数式 $2 x^{2} + 3 x - 3$ 的值为.

查看试题解析
14. 2018年全国滑冰场地与滑雪场地共有1133个．到了2021年，全国滑冰场地与滑雪场地共有2261个，其中滑冰场地比2018年滑冰场地的2倍多232个，滑雪场地比2018年滑雪场地增加了287个．求2018年全国滑冰场地和滑雪场地各有多少个．设2018年全国滑冰场地和滑雪场地分别有x个，y个，依据题意，可列二元一次方程组为．

查看试题解析
15. 如图，在平面直角坐标系 $x O y$ 中，已知点 $A (1 ， 4)$ ， $B (0 ， 2)$ ， $C (- 3 ， 0)$ ， $D (- 1 ， - 1)$ ， $E (5 ， - 3)$ ， $F (4 ， 0)$ ．将线段 $A B$ ， $C D$ ， $E F$ 沿x轴或y轴方向平移后，恰好组成一个首尾相接的三角形．若点 $B$ 与点 $C$ 平移后的对应点均为点O，则线段 $E F$ 需先向左平移个单位长度，再向上平移个单位长度．

查看试题解析
16. 为鼓励学生居家锻炼，李老师组织线上仰卧起坐接力活动.4人为一组，每人自主设定个人目标（单位：次），组内任意2人之间均需接力一场，且每场接力2人都达到个人目标即停止，记录每场接力成绩（2人所做仰卧起坐次数之和）．小贾、小易、小冰、小丁为一组，他们六场接力成绩由小到大依次为86，92，94，98，100，106．若他们设定的个人目标分别记为a，b，c，d，其中 $b < a < c < d$ ，且 $b + d < a + c$ ．根据以上信息，得到三个结论：① $a + b = 86$ ， $c + d = 100$ ；②六场接力成绩由小到大可以依次表示为： $a + b$ ， $b + c$ ， $b + d$ ， $a + c$ ， $a + d$ ， $c + d$ ；③a，b，c，d的值分别为46，40，52，54．其中正确结论的序号是．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\sqrt{6})}^{2} - \sqrt[3]{8} + \sqrt{25}$ ；

(2)、 $\sqrt{3} \times (\sqrt{3} - 1) + | - 2 \sqrt{3} |$ ．

查看试题解析
18. 如图，直线 $l$ 与直线 $A B$ ， $C D$ 分别交于点E，F， $∠ 1$ 是它的补角的3倍， $∠ 1 - ∠ 2 = 90 °$ ．判断 $A B$ 与 $C D$ 的位置关系，并说明理由．

查看试题解析

19. 小明对不等式

\frac{- 2 x - 2}{3} \leq 2 (2 - x)

与

\frac{2 x - 2}{3} \leq 2 (x + 2)

的解法进行比较，如下表：

不等式解法	$\frac{- 2 x - 2}{3} \leq 2 (2 - x)$ ①	$\frac{2 x - 2}{3} \leq 2 (x + 2)$ ②
第一步：去分母，得	$- 2 x - 2 \leq 6 (2 - x)$	$2 x - 2 \leq 6 (x + 2)$
第二步：去括号，得	$- 2 x - 2 \leq 12 - 6 x$	$2 x - 2 \leq 6 x + 12$
第三步：移项，得	$- 2 x + 6 x \leq 12 + 2$	$2 x - 6 x \leq 12 + 2$
第四步：合并同类项，得	$4 x \leq 14$	$- 4 x \leq 14$
第五步：系数化为1，得	____________	____________

(1)、将表格补充完整；

(2)、小明发现：在不等式①和不等式②的求解过程中，前四步中每一步的变形依据相同，第五步的变形依据不同．在第五步中，

不等式①的变形依据是，

不等式②的变形依据是；

(3)、将不等式②的解集表示在数轴上．

查看试题解析

20. 解方程组 ${\begin{array}{l} x - y = 1 \\ 2 x + 3 y = 2 \end{array}$ ．

查看试题解析
21. 下面是小红设计的“过直线外一点作这条直线的平行线”的作图过程．
已知：点C在直线 $A B$ 上，点D在直线 $A B$ 外，且 $∠ D C B = 60 °$ ．

求作：直线 $D E$ ，使得 $D E ∥ A B$ ．

作法：如图，

①在线段 $C D$ 的延长线上任取一点 $M$ ；

②以D为顶点， $D M$ 为一边，通过量角器度量，在 $D M$ 右侧作 $∠ M D E = 60 °$ ；

③将射线 $D E$ 反向延长．

直线 $D E$ 就是所求作的直线．

根据小红的作图过程，解决以下问题：

(1)、补全图形，并完成证明过程；
证明：∵ $∠ M D E = 60 °$ ， $∠ D C B = 60 °$ ，

∴ $∠ M D E = ∠ D C B$ ．

∴ $D E ∥ A B$ （）（填推理的依据）．

(2)、在（1）的条件下，过点C作 $C D$ 的垂线，交直线 $D E$ 于点F．求 $∠ C F E$ 的度数．

查看试题解析
22. 解不等式组 ${\begin{array}{l} 5 x - 1 < 3 (x + 1) ， \\ \frac{1 - x}{3} \leq 1 ， \end{array}$ 并写出它的所有非负整数解．

查看试题解析
23. 北京2022年冬奥会和冬残奥会上，中国运动员获得奖牌的部分统计信息如下．

(1)、冬奥会上，中国代表队共获得15枚奖牌，其中金牌、银牌、铜牌的占比如图1所示，则金牌共有枚，金牌对应扇形的圆心角度数是度；

(2)、冬残奥会上，中国代表队共获得61枚奖牌，其中三类奖牌的数量如图2所示，则金牌共有枚；在图3中，扇形A，B分别表示牌、牌的占比情况．

查看试题解析
24. 如图， $A C$ 平分 $∠ D A B$ ，且 $∠ D A B + ∠ D = 180 °$ ，点 $E$ 在射线 $B C$ 上．若 $∠ B = 95 °$ ， $∠ C A D = 25 °$ ，求 $∠ D C A$ 和 $∠ D C E$ 的度数．

查看试题解析
25. 恩格尔系数是食品支出总额占家庭（或个人）消费或支出总额的比重，常用于反映一个地区人民生活质量的高低，计算公式为：恩格尔系数 $= \frac{食品支出总额}{家庭 (或个人) 消费或支出总额} \times 100 %$ ．对北京市居民家庭1978—2020年的恩格尔系数的有关数据进行收集、整理、描述和分析．下面给出了部分信息：
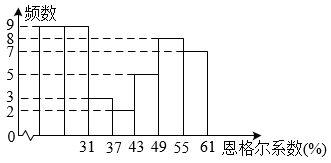
a．北京市居民家庭1978—2020年的恩格尔系数的频数分布直方图（数据分成7组： $19 \leq x < 25$ ， $25 \leq x < 31$ ， $31 \leq x < 37$ ， $37 \leq x < 43$ ， $43 \leq x < 49$ ， $49 \leq x < 55$ ， $55 \leq x \leq 61$ ）：

b．北京市居民家庭1978—2020年的恩格尔系数在 $49 \leq x < 55$ 这一组的是：

49.3 49.6 49.7 51.5 52.1 53.6 53.6 53.7

c．北京市居民家庭1978—2020年的恩格尔系数的统计图：

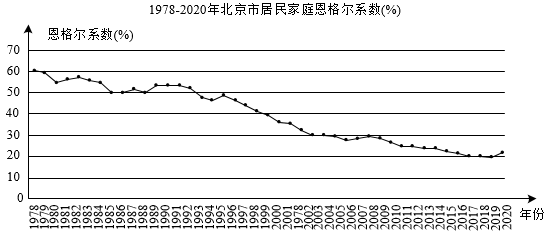
（以上数据来源于《北京统计年鉴（2021）》）

根据以上信息，回答下列问题：

(1)、在1978—2020年中，北京市居民家庭的恩格尔系数共有年低于50%；

(2)、北京市居民家庭1978—2020年的恩格尔系数在年最低（填写年份）；

(3)、下列推断中合理的是．
①1988年，北京市居民家庭的食品支出总额约为家庭（或个人）消费或支出总额的一半；

②1978年以来，北京市居民家庭的恩格尔系数总体呈下降趋势，反映了北京市居民的生活质量逐渐提高．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，已知点 $A (1 ， 0)$ ， $B (0 ， 2)$ ， $C (x ， y)$ ，且 $x y > 0$ ．

(1)、求三角形 $O A B$ 的面积S的值；

(2)、若三角形 $O A C$ 的面积 $S_{1} = 2$ ，三角形 $O B C$ 的面积 $S_{2} = 3$ ，求点C的坐标．

查看试题解析
27. 学校策划了“多读书、读好书、善读书”的主题活动．根据同学们的需求，张老师要为学校图书馆补充一种科普书．某书店的优惠方案如下：

已知该科普书定价30元．

(1)、当购买数量不超过5本时，张老师应选择优惠方案；

(2)、当购买数量超过5本时，张老师如何选择优惠方案？

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于任意两点 $M$ ， $N$ ，给出如下定义：点 $M$ ， $N$ 的横坐标之差的绝对值与纵坐标之差的绝对值的和叫做这两点之间的“直角距离”，记作： $d_{M N}$ ，即点 $M (x_{1} ， y_{1})$ 与点 $N (x_{2} ， y_{2})$ 之间的“直角距离”为 $d_{M N} = | x_{1} - x_{2} | + | y_{1} - y_{2} |$ ．已知点 $A (- 3 ， 2)$ ，点 $B (2 ， 1)$ ．

(1)、A与B两点之间的“直角距离” $d_{A B} =$ ；

(2)、点 $C (0 ， t)$ 为y轴上的一个动点，当 $t$ 的取值范围是时， $d_{A C} + d_{B C}$ 的值最小；

(3)、若动点P位于第二象限，且满足 $d_{A P} \geq d_{B P}$ ，请在图中画出点 $P$ 的运动区域（用阴影表示）．

查看试题解析