北京市门头沟区2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-08-17 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 《北京市“十四五”时期能源发展规划》中提出制定推广新能源车实施方案,到2025年,全市新能源汽车累计保有量力争达到200万辆,将200万用科学记数法表示( )A、2×104 B、2×105 C、2×106 D、2×1073. 有一个数不小于a,这个数在数轴上表示,正确的是( )A、
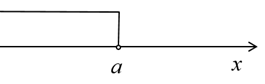 B、
B、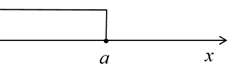 C、
C、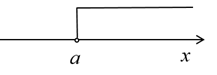 D、
D、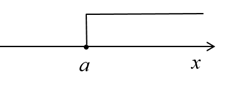 4. 下列命题是假命题的是( )A、同角或等角的余角相等; B、相等的角是对顶角; C、平行于同一条直线的两条直线平行; D、在同一平面内,两条平行直线被第三条直线所截,同位角相等.5. 将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )
4. 下列命题是假命题的是( )A、同角或等角的余角相等; B、相等的角是对顶角; C、平行于同一条直线的两条直线平行; D、在同一平面内,两条平行直线被第三条直线所截,同位角相等.5. 将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( ) A、 B、 C、 D、6. 以下问题,不适合用全面调查的是( )A、调查全班同学的睡眠时间 B、调查某品牌热水器的使用寿命 C、调查某校学生的核算检测结果 D、调查某次航班乘客随身携带物品情况7. 下面从左到右的变形,进行因式分解正确的是( )A、 B、 C、 D、8. 一组从小到大排列的数据:2,5,x,y ,2x,11,这组数据的平均数与中位数都是7,则这组数据的众数是( )A、2 B、5 C、7 D、11
A、 B、 C、 D、6. 以下问题,不适合用全面调查的是( )A、调查全班同学的睡眠时间 B、调查某品牌热水器的使用寿命 C、调查某校学生的核算检测结果 D、调查某次航班乘客随身携带物品情况7. 下面从左到右的变形,进行因式分解正确的是( )A、 B、 C、 D、8. 一组从小到大排列的数据:2,5,x,y ,2x,11,这组数据的平均数与中位数都是7,则这组数据的众数是( )A、2 B、5 C、7 D、11二、填空题
-
9. 如果∠1与∠2互补,∠2与∠3互补,且∠1=125°,那么∠3= °.10. 把方程写成用含y的代数式表示x的形式, .11. 关于x的不等式解集是 , 且解集里面的数是正数, 写出一组满足条件的的值: , .12. 如图,两个四边形均为正方形,根据图形的面积关系,写出一个正确的等式.
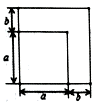 13. 已知数据 , , , 的平均数为10,则数据 , , , 的平均数是 .14. 如图, , 平分交于点 , , 则°.
13. 已知数据 , , , 的平均数为10,则数据 , , , 的平均数是 .14. 如图, , 平分交于点 , , 则°. 15. 如图,要使输出的y值大于100,则输入的最小正整数x是
15. 如图,要使输出的y值大于100,则输入的最小正整数x是 16. 从下面的关系中归纳出规律,然后进行计算:
16. 从下面的关系中归纳出规律,然后进行计算:1 × 3 = 3,而3 = 22 - 1 ;
3 × 5 = 15,而15 = 42 - 1 ;
5 × 7 = 35,而35 = 62 - 1 ;
……
根据如上的规律,第 n 行式子是:( n为正整数),;
并按此规律计算:29 × 31 = .
三、解答题
-
17. 计算: .18. 解不等式组:19. 解方程组:20. 因式分解(1)、(2)、21. 动手操作题: 如图,三角形ABC, 按要求画图并填空,通过测量解决下面的问题:
 (1)、作∠ABC的平分线,交AC于点D;(2)、过点D作BC的平行线,交AB于点E;(3)、写出一对相等的角(角平分线平分的两个角相等除外);(4)、写出一对相等的线段 .22. 已知 , 求代数式的值.23. 补全横线上的内容并在括号中填入适当的理由:如图,ABCD, ∠1=∠2,∠3=∠4;求证:ADBC
(1)、作∠ABC的平分线,交AC于点D;(2)、过点D作BC的平行线,交AB于点E;(3)、写出一对相等的角(角平分线平分的两个角相等除外);(4)、写出一对相等的线段 .22. 已知 , 求代数式的值.23. 补全横线上的内容并在括号中填入适当的理由:如图,ABCD, ∠1=∠2,∠3=∠4;求证:ADBC
证明:∵ABCD(已知)
∴∠4=∠BAE( )
∵∠1=∠2(已知)
∴∠ 1+∠CAF=∠2+∠CAF( )
即 ∠BAE =∠_▲_
∵∠3=∠4 (已知)
∴∠3 =∠_▲_( )
∴ADBC( )
24. 学完因式分解后,小亮同学总结出了因式分解的流程图,如图,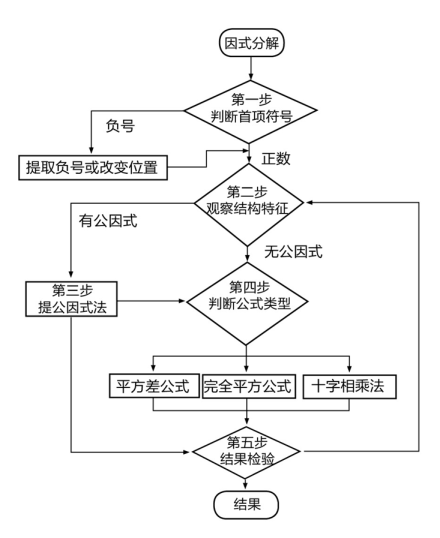
下面是小亮同学的因式分解过程:
①
②
____ ③
回答下面的问题:
(1)、①完成了上面流程图的第步;(2)、②完成了上面流程图的第步;(3)、将③的结果写在横线上 .25. 下面的表格是某景点某天的门票价格及收入情况,这天售出成年人门票和学生门票各多少张?成年人门票
学生门票
售出数量(单位:张)
3000
单价(单位:元/张)
40
20
总价格(单位:元)
78000
26. 阅读材料后解决问题北京市初中开放性科学实践活动是通过网络平台进行活动选课,活动项目包括六个领域,A:自然与环境,B:健康与安全,C:结构与机械,D:电子与控制,E:数据与信息,F:能源与材料.为了了解某区学生自主选课情况,随机抽取了初一部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
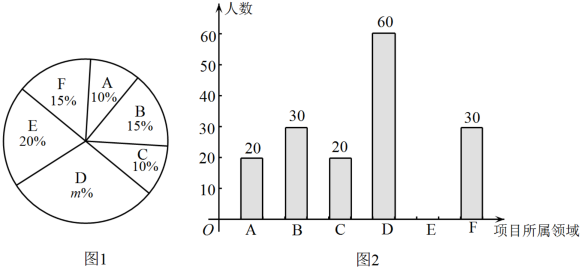 (1)、扇形统计图中值为;(2)、这次被调查的学生共有人;(3)、请将统计图2补充完整;(4)、若该区初一共有学生3000人,根据以上信息估计该区初一学生中选择电子与控制的人数.
(1)、扇形统计图中值为;(2)、这次被调查的学生共有人;(3)、请将统计图2补充完整;(4)、若该区初一共有学生3000人,根据以上信息估计该区初一学生中选择电子与控制的人数.
