辽宁省六校2021-2022学年高二上学期数学期中考试试卷

试卷更新日期：2022-08-17 类型：期中考试

进入出卷网下载

一、单选题

1. 已知 $\vec{a} = (1 ， k ， - 2)$ ， $\vec{b} = (2 k ， 2 ， 4)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则实数 $k$ 的值为（）

A、-2 B、-1 C、2 D、1

查看试题解析
2. 直线 $l_{1}$ ： $2 x + y - 1 = 0$ 与直线 $l_{2}$ ： $4 x + 2 y + 3 + a (2 x + y - 1) = 0$ （实数a为参数）的位置关系是（）

A、 $l_{1}$ 与 $l_{2}$ 相交 B、 $l_{1}$ 与 $l_{2}$ 平行 C、 $l_{1}$ 与 $l_{2}$ 重合 D、 $l_{1}$ 与 $l_{2}$ 的位置关系与a的取值有关

查看试题解析
3. 已知椭圆 $x^{2} + m y^{2} = 1 (m > 0)$ 的焦点在y轴上，长轴长是短轴长的两倍，则 $m =$ （）

A、2 B、1 C、 $\frac{1}{4}$ D、4

查看试题解析
4. 方程 $x \sqrt{1 - y^{2}} + y \sqrt{1 - x^{2}} = 1$ 的对应曲线图形是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在四面体D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列结论正确的是（）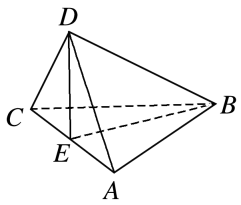

A、平面ABC⊥平面ABD B、平面ABD⊥平面BDC C、平面ABC⊥平面BDE，且平面ADC⊥平面BDE D、平面ABC⊥平面ADC，且平面ADC⊥平面BDE

查看试题解析
6. 方程 $x^{2} - x c o s θ + s i n θ = 0$ 的两个不等实根为m，n，那么过点 $A (m^{2} ， m)$ ， $B (n^{2} ， n)$ 的直线与圆 $x^{2} + y^{2} = 1$ 的位置关系是（）

A、相交 B、相切或相交 C、相切 D、与 $θ$ 的大小有关

查看试题解析
7. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 与直线 $y = k x$ 交于 $A$ ， $B$ 两点，点 $P$ 为 $C$ 上一动点，记直线 $P A$ ， $P B$ 的斜率分别为 $k_{P A}$ ， $k_{P B}$ ， $C$ 的左､右焦点分别为 $F_{1}$ ， $F_{2}$ .若 $k_{P A} \cdot k_{P B} = \frac{1}{4}$ ，且 $C$ 的焦点到渐近线的距离为1，则（）

A、 $a = 4$ B、 $C$ 的离心率为 $\frac{\sqrt{6}}{2}$ C、若 $P F_{1} ⊥ P F_{2}$ ，则 $△ P F_{1} F_{2}$ 的面积为2 D、若 $△ P F_{1} F_{2}$ 的面积为 $2 \sqrt{5}$ ，则 $△ P F_{1} F_{2}$ 为钝角三角形

查看试题解析
8. 设 $F_{1} ， F_{2}$ 是椭圆 $m x^{2} + y^{2} = m (0 < m < 1)$ 的左､右焦点， $P$ 是椭圆上任意一点，若 $\frac{{| P F_{2} |}^{2}}{| P F_{1} |}$ 的最小值是 $\frac{1}{3}$ ，则 $m$ 的值为（）

A、 $\frac{\sqrt{3}}{4}$ B、 $\frac{8}{9}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{1}{9}$

查看试题解析

二、多选题

9. 已知直线 $l ： (t + 2) x + (t - 1) y + 3 = 0$ ，则下述正确的是（）

A、直线 $l$ 的斜率可以等于0 B、直线 $l$ 的斜率一直存在 C、直线 $t = - 0.5$ 时直线的倾斜角为 $\frac{π}{4}$ D、点 $P (1 ， 3)$ 到直线 $l$ 的最大距离为 $2 \sqrt{2}$

查看试题解析
10. 如图，菱形 $A B C D$ 边长为 $2$ ， $∠ B A D = 60 °$ ， $E$ 为边 $A B$ 的中点．将 $△ A D E$ 沿 $D E$ 折起，使 $A$ 到 $A^{'}$ ，且平面 $A^{'} D E ⊥$ 平面 $B C D E$ ，连接 $A^{'} B$ ， $A^{'} C$ ．

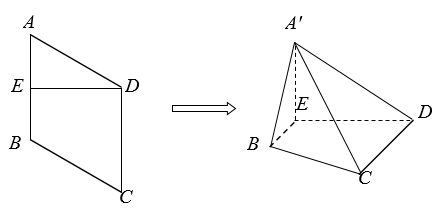
则下列结论中正确的是（）

A、 $B D ⊥ A^{'} C$ B、四面体 $A^{'} C D E$ 的外接球表面积为 $8 π$ C、 $B C$ 与 $A^{'} D$ 所成角的余弦值为 $\frac{3}{4}$ D、直线 $A^{'} B$ 与平面 $A^{'} C D$ 所成角的正弦值为 $\frac{\sqrt{6}}{4}$

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，已知点 $P (x_{0} ， y_{0})$ 和曲线 $C ： x^{2} + m y^{2} = 1$ ，则对于直线 $l ： x_{0} x + m y_{0} y = 1$ 下列说法正确的是（）

A、若 $x_{0} = \frac{1}{2}$ ， $y_{0} = \frac{1}{2}$ ， $m = 1$ ，则直线 $l$ 与曲线 $C$ 没有交点 B、若 $x_{0} = \frac{1}{2}$ ， $y_{0} = 1$ ， $m = - 1$ ，则直线 $l$ 与曲线 $C$ 有二个交点 C、若 $x_{0} = \frac{1}{2}$ ， $y_{0} = \frac{\sqrt{6}}{2}$ ， $m = \frac{1}{2}$ ，则直线 $l$ 与曲线 $C$ 有一个交点 D、直线 $l$ 与曲线 $C$ 的位置关系和 $P$ 在哪里无关

查看试题解析
12. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，长轴长为4，点 $P (\sqrt{2} ， 1)$ 在椭圆内部，点 $Q$ 在椭圆上，则以下说法正确的是（）

A、离心率的取值范围为 $(0 ， \frac{1}{2})$ B、当离心率为 $\frac{\sqrt{2}}{4}$ 时， $| Q F_{1} | + | Q P |$ 的最大值为 $4 + \frac{\sqrt{6}}{2}$ C、存在点 $Q$ 使得 $\vec{Q F_{1}} \cdot \vec{Q F_{2}} = 0$ D、 $\frac{1}{| Q F_{1} |} + \frac{1}{| Q F_{2} |}$ 的最小值为1

查看试题解析

三、填空题

13. 已知点 $P (1 ， 1)$ 和圆 $C ： x^{2} + y^{2} - 2 m x + 4 y + m + 6 = 0$ ，若过点P作圆C的切线有两条，则实数m的取值范围是．

查看试题解析
14. 对任意的实数 $λ$ ，求点 $P (- 2 ， 2)$ 到直线 $(2 + λ) x - (1 + λ) y - 2 （ 3 + 2 λ ） = 0$ 的距离 $d$ 的取值范围为．

查看试题解析
15. 如图，在直角 $△ A B C$ 中， $C = \frac{π}{2}$ ， $B C = 20$ ， $A B = 40$ ，现将其放置在平面 $α$ 的上面，其中点A，B在平面 $α$ 的同一侧，点 $C \in$ 平面 $α$ ， $B C$ 与平面 $α$ 所成的角为 $\frac{π}{6}$ ，则点A到平面 $α$ 的最大距离是.

查看试题解析
16. 设 $P$ 是椭圆 $M ： \frac{x^{2}}{2} + y^{2} = 1$ 上的任一点， $E F$ 为圆 $N ： x^{2} + {(y - 2)}^{2} = 1$ 的任一条直径，则 $\vec{P E} \cdot \vec{P F}$ 的最大值为.

查看试题解析

四、解答题

17. 已知动点 $C$ 与两个定点 $A (0 ， 0) ， B (3 ， 0)$ 的距离之比为 $\frac{\sqrt{2}}{2}$

(1)、求动点 $C$ 的轨迹方程 $T$ .

(2)、若 $△ A B C$ 边 $B C$ 的中点为 $D$ ，求动点 $D$ 的轨迹方程 $T$ .

查看试题解析
18. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，点D在棱 $A_{1} B_{1}$ 上，E，F分别是 $C C_{1}$ ， BC的中点， $A E ⊥ A_{1} B_{1}$ ， $A A_{1} = A B = A C = 2$ ．

(1)、证明： $D F ⊥ A E$ ；

(2)、当D为 $A_{1} B_{1}$ 的中点时，求平面DEF与平面ABC所成锐二面角的余弦值．

查看试题解析
19. 已知圆 $C ： x^{2} + y^{2} - 4 x - 4 y + 4 = 0$ .

(1)、若过点 $P (1 ， 0)$ 的直线 $l$ 与圆 $C$ 相交所得的弦长为 $2 \sqrt{3}$ ，求直线 $l$ 的方程；

(2)、若 $Q$ 是直线 $l^{'} ： 3 x + 4 y + 6 = 0$ 上的动点， $Q A ， Q B$ 是圆 $C$ 的两条切线， $A ， B$ 是切点，求四边形 $Q A C B$ 面积的最小值.

查看试题解析
20. 如图，直四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面 $A B C D$ 为菱形，且 $∠ B A D = 60 °$ ， $A A_{1} = A B$ ， $E$ 为 $B B_{1}$ 的延长线上一点， $D_{1} E ⊥$ 平面 $D_{1} A C$ ，设 $A B = 2$ .

(1)、求二面角 $E - A C - D_{1}$ 的平面角的大小。

(2)、在线段 $D_{1} E$ 上是否存在一点 $P$ ，使 $A_{1} P / /$ 平面 $E A C$ ？若存在，求 $\frac{D_{1} P}{P E}$ 的值；若不存在，请说明理由.

查看试题解析
21. 2020年9月下旬，中国海军为应对台湾海峡的局势，派出3艘舰艇在台湾附近某海域进行实弹演习.某时刻三艘舰艇呈“品”字形列阵(此时舰艇可视作静止的点)，如下图A ， B ， C ，且OA=OB=OC=3，假想敌舰艇在某处发出信号，A点接收到信号的时间比B点接收到信号的时间早 $\frac{4}{v_{0}}$ (注：信号传播速度为 $v_{0}) ，$ C处舰艇保持静默.

(1)、建立适当的坐标系，并求假想敌舰所有可能出现的位置的轨迹方程；

(2)、在A ， B两处舰艇对假想敌舰攻击后，C处敌舰派出无人机到假想敌舰处观察攻击效果，则无人机飞行的距离最少是多少？

查看试题解析
22. 设实数 $k \neq 0$ ，椭圆D： $\frac{x^{2}}{6} + \frac{y^{2}}{2} = 1$ 的右焦点为F，过F且斜率为k的直线交D于P、Q两点，若线段PQ的中为N，点O是坐标原点，直线ON交直线 $x = 3$ 于点M．

(1)、若点P的横坐标为1，求点Q的横坐标；

(2)、求证： $M F ⊥ P Q$ ；

(3)、求 $\frac{| P Q |}{| M F |}$ 的最大值．

查看试题解析