浙江省舟山市属校2021-2022学年八年级下学期期末联考数学试卷
试卷更新日期:2022-08-16 类型:期末考试
一、选择题(共10小题,每小题3分,满分30分)
-
1. 二次根式 在实数范围内有意义,则x可以取的值是( )A、﹣2 B、﹣1 C、0 D、32. 方程的根是( )A、 B、 C、 D、3. 如图,所给图形中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 已知点A(1,y1),B(2,y2),C(﹣3,y3)都在反比例函数y (k>0)的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y2<y1<y3 D、y3<y2<y16. 对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )A、a⊥c B、b⊥c C、a与c相交 D、b与c相交7. 若一组数据x1 , x2 , …xn的平均数为17,方差为2,则另一组数据x1+1,x2+1,…,xn+1的平均数、方差分别为( )A、17,2 B、18,2 C、17,3 D、18,38. 如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 已知点A(1,y1),B(2,y2),C(﹣3,y3)都在反比例函数y (k>0)的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y2<y1<y3 D、y3<y2<y16. 对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )A、a⊥c B、b⊥c C、a与c相交 D、b与c相交7. 若一组数据x1 , x2 , …xn的平均数为17,方差为2,则另一组数据x1+1,x2+1,…,xn+1的平均数、方差分别为( )A、17,2 B、18,2 C、17,3 D、18,38. 如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( ) A、2 B、 C、 D、9. 在以下图形中,根据尺规作图痕迹,不能判断射线AD平分∠BAC的是( )
A、2 B、 C、 D、9. 在以下图形中,根据尺规作图痕迹,不能判断射线AD平分∠BAC的是( ) A、① B、② C、③ D、④10. 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=6 , E,F分别是边AC,BC上的动点,当四边形DEBF为平行四边形时,该四边形的面积是( )
A、① B、② C、③ D、④10. 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=6 , E,F分别是边AC,BC上的动点,当四边形DEBF为平行四边形时,该四边形的面积是( )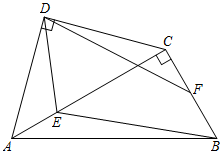 A、3 B、6 C、 D、81
A、3 B、6 C、 D、81二、填空题(本大题共6小题,每小题4分,共24分.)
-
11. 一组数据﹣2,3,2,1,﹣2的中位数为 .12. 已知 的小数部分是a,则 的值是.13. 若一个多边形每一个外角都等于36°,则这个多边形有条边.14. 中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年年收入400美元,预计2018年年收入将达到1000美元,设2016年到2018年该地区居民年人均收入平均增长率为x,可列方程.15. 已知函数的图象与轴、轴分别交于点、 , 与双曲线交于点、若 , 则的值为 .16. 如图,矩形ABCD中,BC=10,∠BAC=30°,若在AC、AB上各取一点M、N,使BM+MN的值最小,求这个最小值 .

三、解答题(本大题共8小题,共66分。)
-
17. 计算:(1)、(2)、18. 在用配方法解一元二次方程4x2﹣12x﹣1=0时,李明同学的解题过程如下:
解:方程4x2﹣12x﹣1=0可化成(2x)2﹣6×2x﹣1=0,
移项,得(2x)2﹣6×2x=1.
配方,得(2x)2﹣6×2x+9=1+9,
即(2x﹣3)2=10.
由此可得2x﹣3=± ∴x1 ,x2 .
晓强同学认为李明同学的解题过程是错误的,因为用配方法解一元二次方程时,首先把二次项系数化为1,然后再配方,你同意晓强同学的想法吗?你从中受到了什么启示?
19. 如图,△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE. (1)、求证:四边形BCFD是平行四边形.(2)、当AB=BC时,若BD=2,BE=3,求AC的长.20. 某中学九年级组织了一次数学计算比赛(禁用计算器),每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图,请根据提供的信息解答下列问题.
(1)、求证:四边形BCFD是平行四边形.(2)、当AB=BC时,若BD=2,BE=3,求AC的长.20. 某中学九年级组织了一次数学计算比赛(禁用计算器),每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图,请根据提供的信息解答下列问题. (1)、把一班竞赛成绩统计图补充完整.(2)、填表:
(1)、把一班竞赛成绩统计图补充完整.(2)、填表:平均数(分)
中位数(分)
众数(分)
一班
82.8
二班
75
100
(3)、请从以下给出的两个方面对这次比赛成绩的结果进行分析:①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
21. 如图,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G,连结BG. (1)、试判断AF与DE的数量关系与位置关系,并证明.(2)、求证:BG平分∠EGF.22. 某购物商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元;为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件衬衫每降价1元,商场平均每天可多售出2件.(1)、每天销售这种衬衫的盈利要达到1200元,则每件衬衫应降价多少元?(2)、每件衬衫降价多少元时,商场每天盈利最多?利润是多少?23. 背景:点A在反比例函数y (k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形.如图1,点A在第一象限内,当AC=4时,小李测得CD=3.
(1)、试判断AF与DE的数量关系与位置关系,并证明.(2)、求证:BG平分∠EGF.22. 某购物商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元;为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件衬衫每降价1元,商场平均每天可多售出2件.(1)、每天销售这种衬衫的盈利要达到1200元,则每件衬衫应降价多少元?(2)、每件衬衫降价多少元时,商场每天盈利最多?利润是多少?23. 背景:点A在反比例函数y (k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形.如图1,点A在第一象限内,当AC=4时,小李测得CD=3.探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系.请帮助小李解决下列问题.
 (1)、求k的值.(2)、设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了x>0时“Z函数”的图象.
(1)、求k的值.(2)、设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了x>0时“Z函数”的图象.①求这个“Z函数”的表达式;
②补画x<0时“Z函数”的图象;
③并写出这个函数的性质(两条即可).
24. 已知:边长为4的正方形ABCD,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=45°,连接EF.求证:EF=BE+DF.思路分析:
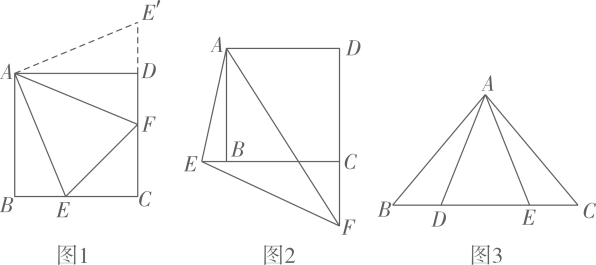 (1)、如图1,∵正方形ABCD中,AB=AD,∠BAD=∠B=∠ADC=90°,
(1)、如图1,∵正方形ABCD中,AB=AD,∠BAD=∠B=∠ADC=90°,∴把△ABE绕点A逆时针旋转90°至△ADE',则F、D、E'在一条直线上,
∠E'AF=度,……
根据定理,可证:△AEF≌△AE'F.
∴EF=BE+DF.
(2)、类比探究:
如图2,当点E在线段CB的延长线上,探究EF、BE、DF之间存在的数量关系,并写出证明过程;(3)、拓展应用:
如图3,在△ABC中,AB=AC,D、E在BC上,∠BAC=2∠DAE.若S△ABC=14,S△ADE=6,求线段BD、DE、EC围成的三角形的面积.