广西壮族自治区北海市2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是二元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 0 \\ 3 x - y = 5 \end{array}$ B、 ${\begin{array}{l} 2 x - y = 1 \\ y = 3 z + 1 \end{array}$ C、 ${\begin{array}{l} x y = 1 \\ x + 2 y = 3 \end{array}$ D、 ${\begin{array}{l} \frac{1}{x} + \frac{1}{y} = 1 \\ x + y = 1 \end{array}$

查看试题解析
2. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $a^{3} + a^{2} = 2 a^{5}$ B、 $2 a (1 - a) = 2 a - 2 a^{2}$ C、 ${(- a b^{2})}^{3} = a^{3} b^{6}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
4. 下列多项式相乘，不能用平方差公式计算的是（）

A、 $(2 x - 3 y) (3 y - 2 x)$ B、 $(- 2 x + 3 y) (- 2 x - 3 y)$ C、 $(x - 2 y) (2 y + x)$ D、 $(x + 3 y) (x - 3 y)$

查看试题解析
5. 在抗击新型冠状病毒肺炎疫情中，某社区志愿者小分队10名队员年龄统计如下表：则这10名队员年龄的中位数、众数分别是（）

年龄（岁）

$18$

$22$

$30$

$35$

$43$

人数

$2$

$3$

$2$

$2$

$1$

A、20岁，35岁 B、26岁，22岁、 C、22岁，26岁 D、30岁，30岁

查看试题解析
6. 如图， $A B$ // $C D ， E F$ 分别交 $A B 、 C D$ 于点E、F， $∠ 1 = 70 °$ ，则 $∠ 2$ 的度数是（）

A、 $70 °$ B、 $90 °$ C、 $100 °$ D、 $110 °$

查看试题解析
7. 已知 $| x + 2 y + 3 | + {(x - y - 3)}^{2} = 0$ ，则 ${(x + y)}^{2022}$ 等于（）

A、 $- 1$ B、1 C、2022 D、 $- 2022$

查看试题解析
8. 对有理数 $x ， y$ 定义新运算：x $\otimes$ y=ax+by+1其中 $a$ ， $b$ 是常数．若 $2 \otimes$ $- 1 = - 3$ ， $3$ $\otimes 3 = 4$ ，则 $a ， b$ 的值分别为（）

A、 $a = 1 ， b = 2$ B、 $a = - 1 ， b = 2$ C、 $a = - 1 ， b = - 2$ D、 $a = 1 ， b = - 2$

查看试题解析
9. 如图， $P$ 是直线 $l$ 外一点， $A$ ， $B$ ， $C$ 三点在直线 $l$ 上，且 $P B ⊥ l$ 于点 $B$ ， $∠ A P C = 90 °$ ，则下列结论：①线段 $A P$ 是点 $A$ 到直线 $P C$ 的距离；②线段 $B P$ 的长是点 $P$ 到直线 $l$ 的距离；③ $P A$ ， $P B$ ， $P C$ 三条线段中， $P B$ 最短；④线段 $P C$ 的长是点 $P$ 到直线 $l$ 的距离.其中正确的是（）

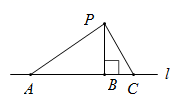A、②③ B、①②③ C、③④ D、①②③④

查看试题解析
10. 观察下列等式：
第1层 $1 + 2 = 3$

第2层 $4 + 5 + 6 = 7 + 8$

第3层 $9 + 10 + 11 + 12 = 13 + 14 + 15$

第4层 $16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24$

在上述数字宝塔中，从上往下数，2022在第（）层．

A、33 B、34 C、44 D、45

查看试题解析

二、填空题

11. 若方程 $x^{2 a - b} - 3 y^{a + b} = 2$ 是关于x、y的二元一次方程，则 $a b =$ ．

查看试题解析
12. 若 $x^{2} + (m - 3) x + 9$ 是完全平方式，则 $m =$ ．

查看试题解析
13. 如图，在 $3 \times 4$ 的正方形网格中已有2个正方形涂黑，再选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，选择的位置共有处．

查看试题解析
14. 为了庆祝中国共产党成立100周年，某校举行“党在我心中”演讲比赛，评委将从演讲内容，演讲能力，演讲效果三个方面给选手打分，各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%，演讲效果占10%，计算选手的综合成绩（百分制）.小婷的三项成绩依次是84，95，90，她的综合成绩是.

查看试题解析
15. 《九章算术》是中国古代的一本重要数学著作，其中有一道方程的应用题：“五只雀、六只燕，共重16两，雀重燕轻．互换其中一只，恰好一样重．问每只雀、燕的重量各为多少?”解：设雀每只x两，燕每只y两，则可列出方程组为。

查看试题解析

三、解答题

16.

(1)、因式分解： $m^{3} - 16 m$ ；

(2)、解下列二元一次方程组： ${\begin{array}{l} 4 x - y = 30 \\ x - 2 y = - 10 \end{array}$

查看试题解析
17. 先化简，再求值： $a (a - 2 b) + {(a + b)}^{2} - (a + b) (a - b)$ ，其中 $a = 1 ， b = - 2$ ．

查看试题解析
18. 网格中 $△ A B C$ 的三个顶点的位置如图所示，现将 $△ A B C$ 平移，使点A变换为点 $A_{1}$ ，点 $B_{1} 、 C_{1}$ 分别是B、C的对应点．

(1)、请画出平移后的 $△ A_{1} B_{1} C_{1}$ （不写画法）；

(2)、将 $△ A_{1} B_{1} C_{1}$ 绕点 $C_{1}$ 顺时针旋转 $90 °$ ，画出旋转后的 $△ A_{2} B_{2} C_{1}$ （不写画法）

(3)、求 $△ A B C$ 的面积．

查看试题解析

19. 据联合国统计，至2022年3月12日，俄乌冲突已导致上千平民伤亡，250万人被迫离开乌克兰，此外，在俄乌冲突与对俄制裁的共同作用下，全球粮食供给、芯片制造、能源价格等均受到不同程度的影响．为了呼吁世界和平，某校举行了以“同护一片蓝天·共享一份和平”为主题的征文比赛，八年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示，并根据图示做了表格统计：

班级	平均数（分）	中位数（分）	众数（分）
八（1）	85	85	a
八（2）	85	b	100

(1)、表中的

a =

，

b =

；

(2)、若已知

S_{2 班}^{2} = 160

，试说明哪个班的成绩比较稳定？为什么？

(3)、若全校参加此次征文比赛复赛的共有100人，请你估计成绩为100分的约有多少人？

查看试题解析

20. 如图，已知AB∥CD，∠B＝70°，CM平分∠BCE，∠MCN＝90°，求∠DCN的度数．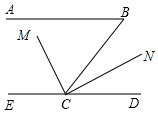

查看试题解析
21. 一般地，我们把如 $a^{2} - 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 的多项式叫做完全平方式．如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．能解决一些与非负数有关的问题或求代数式最大值，最小值等．
例如：分解因式： $x^{2} + 2 x - 3$ ．

原式 $= x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = {(x + 1)}^{2} - 2^{2} = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$ ．

再如：求代数式 $x^{2} + 4 x - 5$ 的最小值．

因为 $x^{2} + 4 x - 5 = x^{2} + 4 x + 4 - 4 - 5 = {(x + 2)}^{2} - 9$

且 ${(x + 2)}^{2} \geq 0$

所以，当 $x = - 2$ 时， $x^{2} + 4 x - 5$ 有最小值，最小值是 $- 9$ ．根据以上材料，回答下列问题：

(1)、分解因式： $a^{2} - 2 a - 3 =$ ；

(2)、代数式 $x^{2} + 2 x + 3$ 的最小值是；

(3)、试说明：无论 $x$ 、 $y$ 取任何实数时，多项式 $x^{2} + y^{2} - 4 x + 2 y + 6$ 的值总为正数．

查看试题解析
22. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种玩具．据了解，8只“冰墩墩”玩具和10只“雪容融”玩具的进价共计2000元；10只“冰墩墩”玩具和20只“雪容融”玩具的进价共计3100元．

(1)、“冰墩墩”和“雪容融”两种玩具每只进价分别是多少元？

(2)、该专卖店计划恰好用3500元购进“冰墩墩”和“雪容融”两种玩具（两种均买），专卖店共有哪几种采购方案？

(3)、若“冰墩墩”和“雪容融”两种玩具每只售价分别是200元、100元．在（2）的条件下，请帮助专卖店选出利润最大的采购方案．

查看试题解析
23. 如图，直线 $A B$ // $C D$ ，点E、F分别是 $A B 、 C D$ 上的动点（点E在点F的右侧），点M为线段 $E F$ 上的一点，点N为射线 $F D$ 上的一点，连接 $M N$ ．

(1)、如图1，若 $∠ B E F = 150 ° ， M N ⊥ E F$ ，求 $∠ M N F$ 的度数．

(2)、如图2，作 $∠ E M N$ 的角平分线 $M Q$ ，且 $M Q$ // $C D$ ．求 $∠ M N F$ 与 $∠ A E F$ 之间的数量关系；

(3)、在（2）的条件下，连接 $E N$ ．且 $E N$ 恰好平分 $∠ B E F ， ∠ M N F = 2 ∠ E N M$ ，求 $∠ E M N$ 的度数．

查看试题解析

年龄（岁）	$18$	$22$	$30$	$35$	$43$
人数	$2$	$3$	$2$	$2$	$1$