湖南省长沙市雨花区2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 为了了解某市初中35000名毕业生的数学成绩，从中抽取20本试卷，每本30份，在这个问题中，样本容量是（）．

A、35000 B、600 C、30 D、20

查看试题解析
2. 下列四个点中，在第二象限的点是（）.

A、（2，-3） B、（2，3） C、（-2，3） D、（-2，-3）

查看试题解析
3. 化简 $\sqrt{4^{2}}$ 的结果是（）

A、 $- 4$ B、4 C、 $\pm 4$ D、2

查看试题解析
4. 如图，已知直线 $a / / b$ ， $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数为（）

A、 $140 °$ B、 $130 °$ C、 $50 °$ D、 $40 °$

查看试题解析
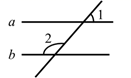5. 关于x的不等式 $2 x + m > 3$ 的解如图所示，则m的值为（）．

A、 $- 1$ B、 $- 5$ C、1 D、5

查看试题解析
6. 在一次慈善基金捐款活动中，某单位对捐款金额分别是人民币100元、200元、300元、400元和500元的人数进行了统计，制成如下统计图．小明从该统计图获得四条信息，其中正确的是（）

A、捐款金额越高，捐款的人数越少 B、捐款金额为500元的人数最多 C、捐款金额为400元的人数比捐款金额为200元的人数要少 D、捐款金额为100元的人数最少

查看试题解析
7. 把一些图书分给几名同学，如果每人分3本，那么余8本；如果前面的每名同学分5本，那么最后一人至少有一本，但不到3本．那么这些图书有（）．

A、26本 B、25本 C、24本 D、23本

查看试题解析
8. 已知x，y满足方程组 ${\begin{array}{l} x + m = 4 \\ y - 5 = m \end{array}$ ，则无论m取何值，x，y恒有关系式（）．

A、 $x + y = 1$ B、 $x + y = - 1$ C、 $x + y = 9$ D、 $x - y = 9$

查看试题解析
9. 已知线段AB的长为10cm，点A、B到直线l的距离分别为5cm和3cm，则符合条件的直线l共有（）

A、4条 B、3条 C、2条 D、1条

查看试题解析
10. 在平面直角坐标系中，若 $A (1 ， 4)$ ， $B (3 ， 2)$ ，将线段AB平移到CD，且C，D都在坐标轴上，则C点坐标为（）．

A、 $(2 ， 0)$ 或 $(0 ， - 2)$ B、 $(0 ， 2)$ 或 $(- 2 ， 0)$ C、 $(2 ， 0)$ 或 $(- 2 ， 0)$ D、 $(0 ， 2)$ 或 $(0 ， - 2)$

查看试题解析

二、填空题

11. 已知 $\sqrt[3]{1.12} \approx 1.038$ ，则 $\sqrt[3]{1120} \approx$ ．

查看试题解析
12. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表，则表中a= ， b= ， c= ．
月均用水量/t
$2 \leq x < 3$
$3 \leq x < 4$
$4 \leq x < 5$
$5 \leq x < 6$
$6 \leq x < 7$
$7 \leq x < 8$
$8 \leq x < 9$
频数
2
12
a
10
b
3
2
百分比
4％
24％
c
20％
12％
6％
4％

查看试题解析
13. 若关于x的不等式组 ${\begin{cases} \end{cases} \begin{array}{l} x ＞ 2 \\ x ＞ m \end{array}$ 的解集是 $x > 2$ ，则m的取值范围是．

查看试题解析
14. 二元一次方程 $3 x + 4 y = 11$ 的正整数解为．

查看试题解析
15. 如图，直线AB、CD相交于点O，OE平分 $∠ B O D$ ， OF平分 $∠ C O E$ ．若 $∠ A O C = 76 °$ ，则 $∠ B O F$ 的度数为°．

查看试题解析
16. 如图， $∠ A O C = 30 °$ ， $∠ B O C = 150 °$ ， OD为 $∠ B O A$ 的平分线，若A点可表示为 $(2 ， 30 °)$ ， B点可表示为 $(4 ， 150 °)$ ，则D点可表示为．

查看试题解析

三、解答题

17. 解不等式： $2 - \frac{x + 2}{3} > x + \frac{x - 1}{2}$ ．

查看试题解析
18. 已知一个正数m的两个不相等的平方根是a+6与2a﹣9．

(1)、求a的值；

(2)、求这个正数m；

(3)、求关于x的方程ax²﹣16＝0的解．

查看试题解析
19. 如图， $△ A B C$ 的顶点都在平面直角坐标系中的坐标轴上， $△ A B C$ 的面积 $S_{△ A B C} = 24$ ， $O A = O B$ ， $B C = 12$ ，求 $△ A B C$ 三个顶点的坐标．

查看试题解析
20. 随着社会的发展，通过微信朋友圈发布自己每天行走的步数已经成为一种时尚．“健身达人”小陈为了了解他的好友的运动情况．随机抽取了部分好友进行调查，把他们6月1日那天行走的情况分为四个类别：A（0～5000步）（说明：“0～5000”表示大于等于0，小于等于5000，下同），B（5001～10000步），C（10001～15000步），D（15000步以上），统计结果如图所示：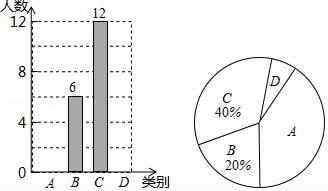

请依据统计结果回答下列问题：

(1)、本次调查中，一共调查了位好友．

(2)、已知A类好友人数是D类好友人数的5倍．
①请补全条形图；

②扇形图中，“A”对应扇形的圆心角为 ▲ 度．

③若小陈微信朋友圈共有好友150人，请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步？

查看试题解析
21. 先阅读，然后解方程组 ${\begin{array}{l} x - y - 1 = 0 \\ 4 (x - y) - y = 5 \end{array}$ .
解方程组时，可由①得x﹣y=1③，然后再将③代入②得4×1﹣y=5，求得y=﹣1，从而进一步求得 ${\begin{array}{l} x = 0 \\ y = - 1 \end{array}$ ，这种方法被称为“整体代入法”.
请用这样的方法解方程组 ${\begin{array}{l} 2 x - y - 2 = 0 \\ \frac{6 x - 3 y + 4}{5} + 2 y = 12 \end{array}$ .

查看试题解析
22. 如图，已知CE⊥AB，MN⊥AB，∠EDC+∠ACB＝180°.求证：∠1＝∠2.

查看试题解析
23. 某电器经营业主两次购进一批同种型号的挂式空调和电风扇，第一次购进8台空调和20台电风扇；第二次购进10台空调和30台电风扇.

(1)、若第一次用资金25600元，第二次用资金32800元，求挂式空调和电风扇每台的采购价各是多少元？

(2)、在（1）的条件下，若该业主计划再购进这两种电器50台，而可用于购买这两种电器的资金不超过30000元，问该经营业主最多可再购进空调多少台？

查看试题解析
24. 如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的“关联方程”．

(1)、判断一元一次方程 $x - (3 x + 1) = - 6$ 是否是一元一次不等式组 ${\begin{array}{l} - x + 1 > x - 5 \\ 3 x - 1 > - x + 2 \end{array}$ 的“关联方程”？

(2)、若不等式组 ${\begin{array}{l} - x + 1 > x - 5 \\ 3 x - 1 > - x + 2 \end{array}$ 的一个“关联方程”的根是整数，写出一个这样的“关联方程”；

(3)、若方程 $3 - x = 2 x$ ， $3 + x = 2 (x + \frac{1}{2})$ 都是关于x的不等式组 ${\begin{array}{l} x < 2 x - m \\ x - 2 \leq m \end{array}$ 的“关联方程”，直接写出m的取值范围．

查看试题解析
25. 问题情境：
我们知道，“如果两条平行直线被第三条直线所截，截得的同位角相等，内错角相等，同旁内角互补”，所以在某些探究性度量中通过“构造平行线”可以起到转化角的作用．已知三角板ABC中，∠BAC＝60°，∠B＝30°，∠C＝90°，长方形DEFG中，DE//GF．

问题初探：

如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，则∠EMC的度数是多少呢？若过点C作CH//GF，则CH//DE，这样就将∠CAF转化为∠HCA，∠EMC转化为∠MCH，从而可以求得∠EMC的度数为…．

(1)、请你直接写出：∠CAF＝°，∠EMC＝°．

(2)、类比再探：若将将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想∠EMC与∠CAF的数量关系？并说明理由．

(3)、方法迁移：请你猜想（1）（2）解决问题的思路，在图（2）中探究∠BAG与∠BMD的数量关系？并说明理由．

查看试题解析

月均用水量/t	$2 \leq x < 3$	$3 \leq x < 4$	$4 \leq x < 5$	$5 \leq x < 6$	$6 \leq x < 7$	$7 \leq x < 8$	$8 \leq x < 9$
频数	2	12	a	10	b	3	2
百分比	4％	24％	c	20％	12％	6％	4％