湖南省永州市宁远县2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，属于二元一次方程的是（）

A、 $4 x - y = 5$ B、 $3 a - b = 2 c$ C、 $x^{2} = 3$ D、 $\frac{1}{x} + 3 = 0$

查看试题解析
2. 已知方程组 ${\begin{array}{l} 2 x + y = 7 \\ x + 2 y = 8 \end{array}$ ，则 $x - y$ 的值是（）

A、5 B、1 C、0 D、 $- 1$

查看试题解析
3. 下列式子正确的是（）

A、 $a^{3} \cdot a^{2} = a^{5}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 ${(a b)}^{2} = a b^{2}$ D、 $a^{3} + a^{2} = a^{5}$

查看试题解析
4. 下列图形中，是轴对称图形且对称轴条数最多的是（）

A、 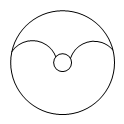B、 C、 D、

查看试题解析
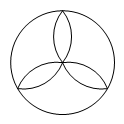5. 下列各式从左到右的变形中，是因式分解的为（）

A、 $a x + b x + c = x (a + b) + c$ B、 $x^{2} - 1 = (x + 1) (x - 1)$ C、 $x (a - b) = a x + b x$ D、 $x^{2} - 1 + y^{2} = (x + 1) (x - 1) + y^{2}$

查看试题解析
6. 已知5⁴－1能被20~30之间的两个整数整除，则这两个整数是（）

A、25，27 B、26，28 C、24，26 D、22，24

查看试题解析
7. 如图，直线a，b被c所截，则 $∠ 1$ 与 $∠ 2$ 是（）

A、同位角 B、内错角 C、同旁内角 D、邻补角

查看试题解析
8. 两个全等的正六边形如图摆放，与△ABC面积不同的一个三角形是（）

A、△ABD B、△ABE C、△ABF D、△ABG

查看试题解析
9. 甲、乙、丙、丁四名学生4次数学测验成绩的平均数相同，方差分别是 $S_{甲}^{2} = 36$ ， $S_{乙}^{2} = 24$ ， $S_{丙}^{2} = 25.5$ ， $S_{丁}^{2} = 6$ ，则这四名学生的数学成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
10. 如图，把一张长方形纸片沿 $E F$ 折叠后，点 $D$ 、 $C$ 分别落在点D′、C′的位置．若 $∠ E F B = 65 °$ ，则∠AED′的大小是（）

A、 $70 °$ B、 $65 °$ C、 $50 °$ D、 $25 °$

查看试题解析

二、填空题

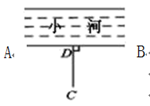
11. 计算：（﹣a³）²•a⁶＝．

查看试题解析
12. 若实数x，y满足方程组 ${\begin{array}{l} x - y = - 4 ， \\ x + y = 2 ， \end{array}$ 则 $(2 x + y)^{2022} =$ ．

查看试题解析
13. 已知 $a b = 2$ ， $a - b = - 4$ ，则 $a^{2} b - a b^{2} =$ ．

查看试题解析
14. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
15. 如图，为了把河中的水引到 $C$ 处，可过点 $C$ 作 $C D ⊥ A B$ 于 $D$ ，然后沿 $C D$ 开渠，这样做可使所开的渠道最短，这种设计的依据是．

查看试题解析
16. 如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3=度

查看试题解析
17. 若x₁ ， x₂ ， x₃的平均数为3，则5x₁+1，5x₂+2，5x₃+3的平均数为.

查看试题解析
18. 两边都平行的两个角，其中一个角的度数是另一个角的3倍少 $20 °$ ，这两个角的度数分别是.

查看试题解析

三、解答题

19. 解下列方程组：

(1)、 ${\begin{array}{l} x + 3 y = 10 \\ x = 2 y \end{array}$

(2)、 ${\begin{array}{l} 3 x + 2 y = 8 \\ 6 x - y = 11 \end{array}$

查看试题解析
20. 分解因式：

(1)、 $- 8 a x^{2} + 16 a x y - 8 a y^{2}$

(2)、 ${(x^{2} + 9 y^{2})}^{2} - 36 x^{2} y^{2}$ ；

查看试题解析
21. 已知（x²+mx+n）（x²﹣3x+2）中，不含x³项和x项，求m，n的值．

查看试题解析
22. 完成下面的证明：如图，BE平分∠ABD，DE平分∠BDC，且∠α+∠β＝90°，求证：AB∥CD．
完成推理过程：
BE平分∠ABD（已知），
∴∠ABD＝2∠α（  ）．
∵DE平分∠BDC（已知），
∴∠BDC＝2∠β（  ）
∴∠ABD+∠BDC＝2∠α+2∠β＝2（∠α+∠β）（  ）
∵∠α+∠β＝90°（已知），
∴∠ABD+∠BDC＝180°（  ）．
∴AB∥CD（  ）．

查看试题解析
23. 如图所示， $Δ A B C$ 的顶点坐标分别为 $A (- 3 ， 5) ， B (- 6 ， 1) ， C (- 1 ， 3)$

(1)、作出 $Δ A B C$ 关于 $x$ 轴对称的图形 $Δ A_{1} B_{1} C_{1}$ ；

(2)、写出 $A_{1} ， B_{1} ， C_{1}$ 的坐标；

(3)、求 $Δ A B C$ 的面积．

查看试题解析
24. 为有效防控新冠肺炎疫情，小明的妈妈让他到药店购买口罩和酒精湿巾，若购买2包口罩和3包酒精湿巾共需19元，购买5包口罩和1包酒精湿巾共需28元．

(1)、求每包口罩和每包酒精湿巾的单价；

(2)、妈妈给了小明50元钱全部用于购买此口罩和酒精湿巾（且都要购买），请问小明有哪几种购买方案？

查看试题解析
25. 某次学生夏令营活动，有小学生、初中生、高中生和大学生参加，共200人，各类学生人数比例见扇形统计图．

(1)、参加这次夏令营活动的初中生共有多少人？

(2)、活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款．结果小学生每人捐款 5 元，初中生每人捐款 10 元，高中生每人捐款 15 元，大学生每人捐款 20 元．问平均每人捐款是多少元？

(3)、在（2）的条件下，把每个学生的捐款数额（以元为单位）——记录下来，则在这组数据中，众数是多少？

查看试题解析
26. 如图1，AB∥CD， $∠ P A B = 130 °$ ， $∠ P C D = 120 °$ ，求 $∠ A P C$ 的度数．

小明的思路是：过 $P$ 作 $P E / / A B$ ，通过平行线性质来求 $∠ A P C$ ．

(1)、按小明的思路，求 $∠ A P C$ 的度数；

(2)、（问题迁移）
如图2， $A B / / C D$ ，点 $P$ 在射线 $O M$ 上运动，记 $∠ P A B = α$ ， $∠ P C D = β$ ，当点 $P$ 在 $B$ 、 $D$ 两点之间运动时，问 $∠ A P C$ 与 $α$ 、 $β$ 之间有何数量关系？请说明理由；

(3)、（问题应用）
在（2）的条件下，如果点 $P$ 在 $B$ 、 $D$ 两点外侧运动时（点 $P$ 与点 $O$ 、 $B$ 、 $D$ 三点不重合），请直接写出 $∠ A P C$ 与 $α$ 、 $β$ 之间的数量关系（并画出相应的图形）．

查看试题解析