湖南省娄底市娄星区2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-16 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列图形中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各方程是二元一次方程的是（）

A、 $\frac{x - 2}{3} + 2 y = 4$ B、 $3 x y + 9 = 8$ C、 $3 x + \frac{1}{y} = 1$ D、 $x^{2} = 5 y + 1$

查看试题解析
3. 在同一平面内，不重合的两条直线可能的位置关系是（）

A、平行 B、相交 C、平行或相交 D、不能确定

查看试题解析
4. 下列运算正确的是（）

A、 $3 a^{2} + 2 a = 5 a^{2}$ B、 $4 a^{3} \cdot 3 a^{2} = 12 a^{6}$ C、 $- 8 a^{7} \div 4 a = 2 a^{6}$ D、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$

查看试题解析
5. 下列等式从左到右的变形，属于因式分解的是（）

A、a（x－y）＝ax－ay B、（x＋1）（x＋3）＝x²＋4x＋3 C、x²＋2x＋1＝（x－1）² D、x³－4x＝x（x＋2）（x－2）

查看试题解析
6. 如果 $x^{2} + k x + \frac{1}{4}$ 是一个完全平方式，则 $k$ 为（）

A、1 B、 $± 1$ C、-1 D、4

查看试题解析
7. 计算 $- x^{2} \cdot (- x)^{2}$ 的结果是（）

A、 $- x^{4}$ B、 $- 2 x^{2}$ C、 $x^{4}$ D、 $2 x^{4}$

查看试题解析
8. 《孙子算经》是中国古代重要的数学著作，纸书大约在一千五百年前，其中一道题，原文是：“今三人共车，两车空；二人共车，九人步．问人与车各几何？”意思是：现有若干人和车，若每辆车乘坐3人，则空余两辆车：若每辆车乘坐2人，则有9人步行，问人与车各多少？设有x人，y辆车，可列方程组为（）

A、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x}{2} + 9 = y \end{array}$ B、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x - 9}{2} = y \end{array}$ C、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x - 9}{2} = y \end{array}$ D、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x}{2} - 9 = y \end{array}$

查看试题解析
9. 如图，下面哪个条件不能判断EF∥DC的是（）

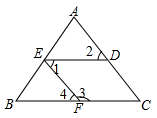A、∠1＝∠2 B、∠4＝∠C C、∠1+∠3＝180° D、∠3+∠C＝180°

查看试题解析
10. 如图所示，点C到AB所在的直线的距离是指图中线段（）的长度．

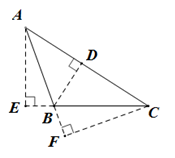A、AE B、CF C、BD D、BE

查看试题解析
11. 如图，将直角△ABC沿AB方向平移2cm得到△DEF，CH=2cm，EF=4cm，下列结论：①BH∥EF；②AD=BE；③∠C=∠BHD；④阴影部分的面积为6cm² ．其中正确的是（）

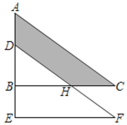A、①②③④ B、②③④ C、①②③ D、①②④

查看试题解析
12. 如图，在边长为a的正方形中挖掉一个边长为b的小正方形，把余下的部分拼成一个长方形（无重叠部分），通过计算两个图形中阴影部分的面积，可以验证的一个等式是（）

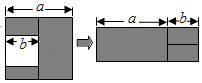A、a²﹣b²＝（a+b）（a﹣b） B、a（a﹣b）＝a²﹣ab C、（a﹣b）²＝a²﹣2ab+b² D、a（a+b）＝a²+ab

查看试题解析

二、填空题

13. 计算2022²﹣2023×2021＝．

查看试题解析
14. 某校七年级一班学生中，13岁的有6人，12岁的有30人，11岁的有6人，这个班的平均年龄是岁．

查看试题解析
15. 若 $x^{m} = 3$ ， $x^{n} = 2$ ，则 $x^{2 m + n}$ ＝．

查看试题解析
16. 如图， $A B // C D$ ，点 $P$ 为直线 $C D$ 上的任意一点，三角形 $P A B$ 的面积为6， $A B = 4$ ，则直线 $A B$ 与 $C D$ 的距离为.

查看试题解析
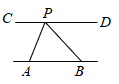17. 如图，由八块相同的长方形地砖拼成一个大长方形，则每块小长方形地砖的面积是．

查看试题解析
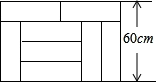18. 如图，将三角形OAB绕点O逆时针旋转55°后得到三角形OCD，此时 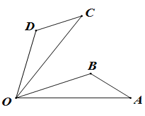$C D ∥ O B$ ，若 $∠ A O B = 20 °$ ，则 $∠ A$ 的度数是．

查看试题解析

三、解答题

19. 作图题：如图为正方形网格，三角形ABC的三个顶点均在格点上，现将三角形ABC平移，把点 $A$ 平移到点 $A_{1}$ ， B、C的对应点分别为点 $B_{1}$ 、 $C_{1}$ ．

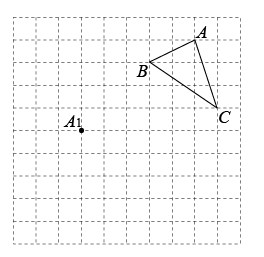(1)、请画出平移后的三角形A₁B₁C₁（不写作法）；

(2)、将三角形A₁B₁C₁绕点 $C_{1}$ 顺时针旋转 $90 °$ ，画出旋转后的三角形A₂B₂C₁（不写作法）．

查看试题解析
20. 如图，已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B$ ， $∠ 4 = 65 °$ ，求∠ACB的度数．填空并填写理由：
因为 $∠ 1 + ∠ 2 = 180 °$ ，
$∠ 1 + ∠ D F E = 180 °$ ，
所以 $∠ 2 = ∠ D F E$ ，（   ）
因此有： $A B / / E F$ ，（   ）
所以 $∠ 3 = ∠ A D E$ （    ）
又因为 $∠ 3 = ∠ B$ ，
所以∠ADE =  ▲   ，
因此 $D E / / B C$ ，（    ）
所以 $∠ A C B = ∠ 4$ ，（   ）
而 $∠ 4 = 65 °$ ，
所以 $∠ A C B = 65 °$ ．

查看试题解析
21. 解下列方程组

(1)、 ${\begin{cases} x - 2 y = 3 ① \\ 3 x + y = 2 ② \end{cases}$

(2)、 ${\begin{cases} 2 x + 3 y = - 14 ① \\ \frac{x + 1}{3} = \frac{y + 4}{5} ② \end{cases}$

查看试题解析
22. 因式分解

(1)、 $4 x^{2} + 20 x + 25$ ；

(2)、 $(a^{2} - 9 b^{2}) + (a - 3 b)$ ．

查看试题解析
23. 为了发展体育运动，培养学生的综合能力，某学校成立了足球队、篮球队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩记录如下表：
射击次序（次）
一
二
三
四
五
六
七
八
九
十
甲的成绩（环）
8
9
7
9
8
6
7
a
10
8
乙的成绩（环）
6
7
9
7
9
10
8
7
7
10

(1)、经计算甲和乙的平均成绩都是8环，请求出表中的a＝；

(2)、甲射击成绩的中位数和乙射击成绩的众数各是多少？

(3)、若甲成绩的方差是1.2，请求出乙成绩的方差，判断甲、乙两人谁的成绩更为稳定？

查看试题解析
24. 求代数式的值：

(1)、先化简，再求值： ${(x - 2 y)}^{2} - 2 (x + y) (x - y) - 6 y^{2}$ ，其中 $x = 2$ ， $y = - \frac{1}{2}$ ；

(2)、已知 $(a + b)^{2} = 9$ ， $(a - b)^{2} = 4$ ，求 $a^{2} + b^{2}$ 的值．

查看试题解析
25. 娄底市出租车收费规定：起步价所包含的路程为0～1.5千米，超过1.5千米的部分按每千米另收费．
刘同学说：“我乘出租车从市政府到娄底汽车站走了4.5千米，付车费11元．”
李同学说：“我乘出租车从市政府到娄底火车站走了6.5千米，付车费15元．”
问：

(1)、出租车的起步价是多少元？超过1.5千米后每千米收费多少元？

(2)、小张乘出租车从家里到娄底南站（高铁站）走了9.5千米，应付车费多少元？

查看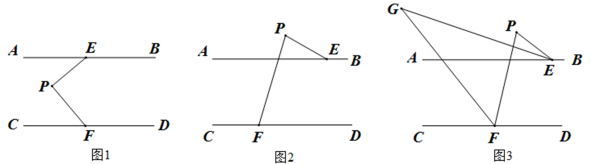试题解析
26.

(1)、（问题）如图1，若AB $∥$ CD，∠AEP=40°，∠PFD=130°，求∠EPF的度数；

(2)、（问题迁移）如图2，AB $∥$ CD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；

(3)、（问题拓展）如图3所示，在⑵的条件下，已知∠EPF=α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．

查看试题解析

射击次序（次）	一	二	三	四	五	六	七	八	九	十
甲的成绩（环）	8	9	7	9	8	6	7	a	10	8
乙的成绩（环）	6	7	9	7	9	10	8	7	7	10